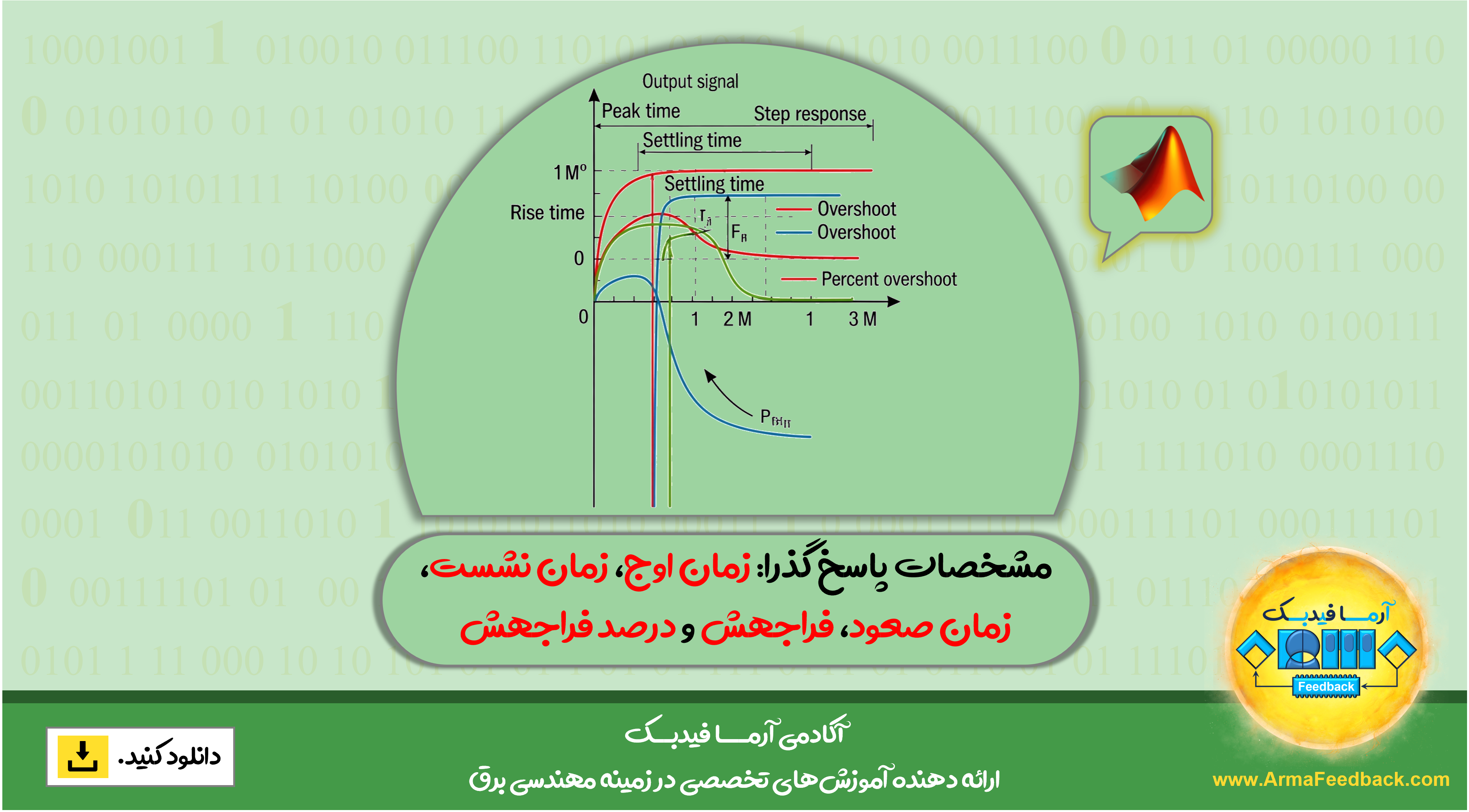
مشخصات پاسخ گذرا: زمان اوج، زمان نشست، زمان صعود، فراجهش و درصد فراجهش
سر فصل مطالب:
در این مقاله آموزشی، توضیحاتی در مورد مشخصات پاسخ گذرا ارائه میدهیم: زمان اوج، زمان نشست، زمان خیز، فراجهش و درصد فراجهش.
مقادیر زمان اوج، زمان نشست، زمان خیز و درصد فراجهش برای طراحی کنترل بسیار مهم هستند. ما اغلب رفتار مطلوب سیستم را بر حسب مقادیر این پارامترهای پاسخ گذرا مشخص میکنیم. سپس، بر اساس مقادیر مطلوب این پارامترها، سیستم کنترل را طراحی میکنیم. همچنین، برای سیستمهای مرتبه دوم، میتوانیم نسبت میرایی، فرکانس طبیعی، پهنای باند و برخی دیگر از ویژگیهای سیستمهای دینامیکی را با مقادیر زمان اوج، زمان نشست، زمان خیز و درصد فراجهش مرتبط کنیم.
در این مقاله آموزشی، ما رسماً زمان اوج (peak time)، زمان نشست (settling time)، زمان صعود (rise time) و درصد فراجهش (percent overshoot) را تعریف میکنیم و توضیحات گرافیکی از این پارامترهای مهم ارائه میدهیم.
محاسبه پاسخ گذرا ( Transient Response ) در متلب:
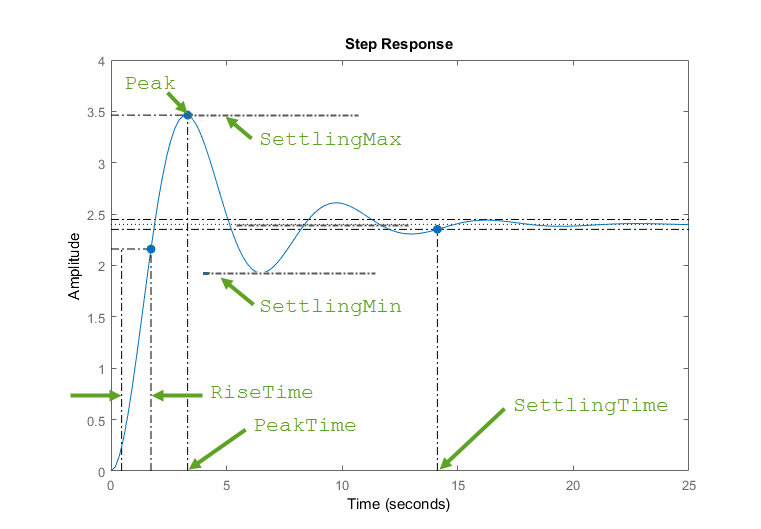
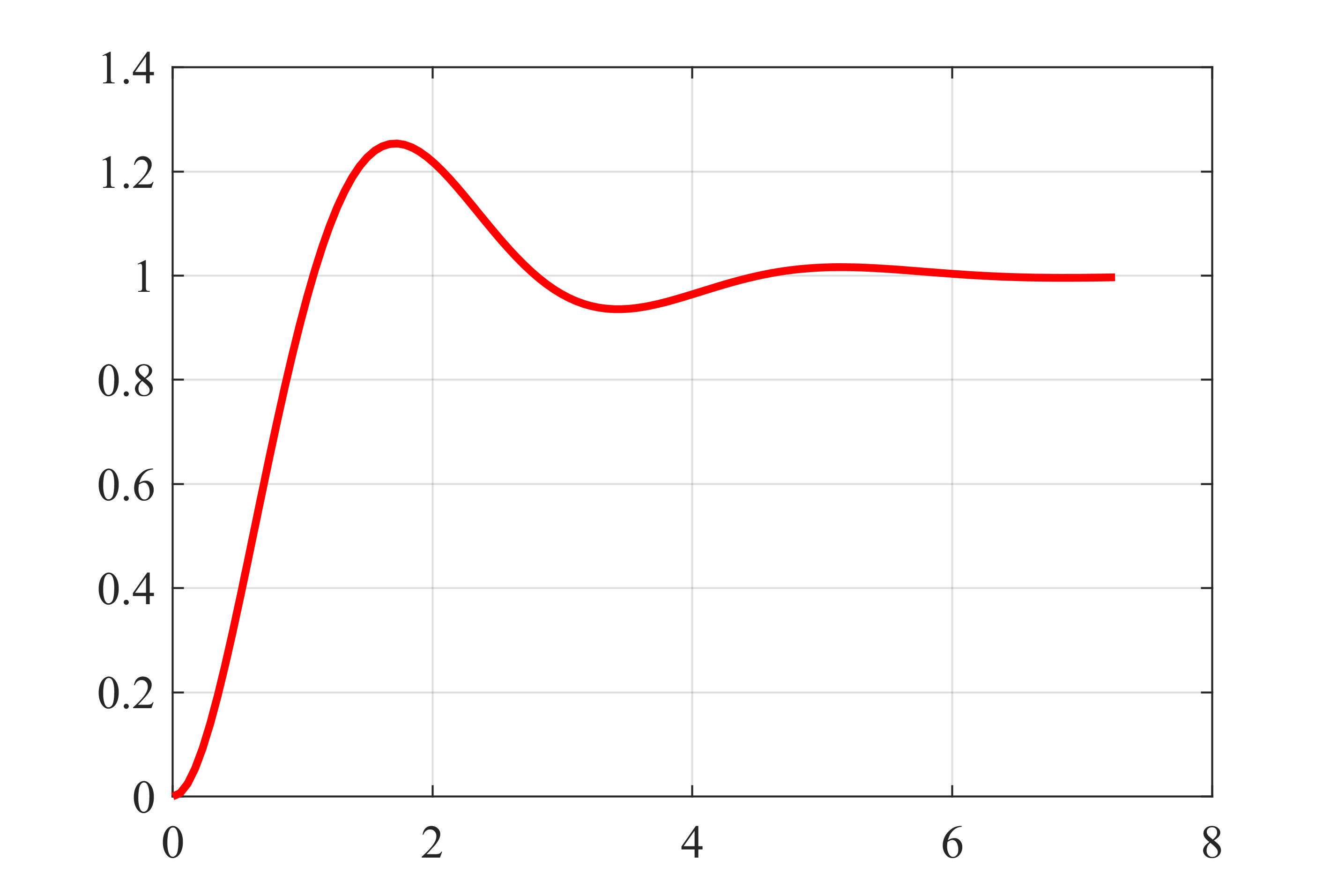
پاسخ پله که در شکلهای زیر نشان داده شده است، برای سیستم زیر محاسبه شده است.
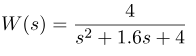
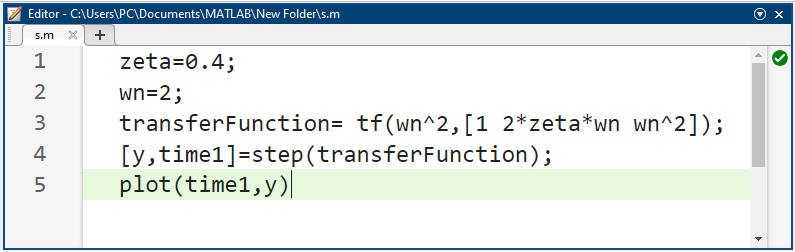
پاسخ پله با استفاده از کد متلب زیر محاسبه میشود.
۲. زمان نشست
زمان نشست که با ts نشان داده میشود، به صورت گرافیکی در شکل ۱ در زیر توضیح داده شده است. مقدار نهایی یا حالت پایدار پاسخ سیستم با yss نشان داده شده است.
نتیجه شبیهسازی: توضیح زمان نشست یک سیستم دینامیکی
تعریف زمان نشست ۲٪: زمان نشست ts به عنوان زمان لازم برای ورود و ماندن پاسخ گذرا در محدوده ۲٪ از مقدار حالت پایدار یا نهایی تعریف میشود.
در اینجا چند نکته مهم در مورد زمان نشست آورده شده است. اول از همه، به شیوهای مشابه و با روحیهای مشابه تعریف بالا، میتوانیم زمان نشست ۵٪ را نیز تعریف کنیم. سپس، بدیهی است که تعریف زمان نشست به طور ضمنی فرض میکند که سیستم به یک حالت پایدار محدود میرسد. این به طور ضمنی نشان میدهد که سیستم زیربنایی به طور مجانبی پایدار است. همانطور که در شکل ۱ نشان داده شده است، میتوانیم زمان نشست را ابتدا با رسم یک خط افقی که از مقدار حالت پایدار پاسخ شروع میشود، بسازیم. سپس، این خط را ۲٪ جابجا میکنیم تا یک بازه یا یک تونل به دست آوریم. سپس به دنبال نقطه تقاطع پاسخ سیستم با خط افقی ۲٪ هستیم به طوری که پاسخ پس از نقطه تقاطع وارد تونل شود و هرگز از آن خارج نشود. زمان مربوط به نقطه تقاطع، زمان نشست ما است.
در نهایت، زمان نشست و همچنین سایر پارامترهای پاسخ گذرا که در این پست تعریف شدهاند، میتوانند نه تنها برای سیستمهای مرتبه دوم، بلکه برای سیستمهای با مرتبههای دلخواه نیز تعریف شوند.
۳. زمان اوج بار
زمان اوج بار یکی دیگر از ویژگیهای مهم پاسخ گذرای سیستم است. معمولاً به صورت زیر تعریف میشود:
تعریف زمان اوج: زمان اوج که با tp نشان داده میشود، به عنوان زمان لازم برای رسیدن سیستم به حداکثر فراجهش تعریف میشود.
زمان اوج در شکل ۲ در زیر نشان داده شده است.

۴. زمان خیزش
تعریف زمان خیزش: زمان خیزش، زمان لازم برای رسیدن پاسخ سیستم از ۱۰٪ به ۹۰٪ مقدار نهایی یا حالت پایدار آن است.
زمان خیزش در شکل ۳ زیر توضیح داده شده است. مقدار نهایی یا حالت پایدار پاسخ سیستم با yss نشان داده شده است. ۱۰٪ و ۹۰٪ از مقادیر نهایی به ترتیب با ۰.۱yss و ۰.۹ yss نشان داده شدهاند.

۵. فراجهش و درصد فراجهش
حداکثر فراجهش را میتوان به صورت زیر تعریف کرد:
تعریف (حداکثر) فراجهش: (حداکثر) فراجهش که با Mp نشان داده میشود، به صورت زیر تعریف میشود
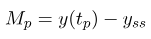
که در آن tp زمان اوجی است که در آن پاسخ پله به حداکثر مقدار خود میرسد، و yss مقدار نهایی یا ثابت پاسخ پله است. (حداکثر) فراجهش در شکل ۴ در زیر نشان داده شده است.

تعریف درصد (حداکثر) فراجهش: درصد (حداکثر) فراجهش که با Mp% نشان داده میشود، به صورت زیر تعریف میشود:
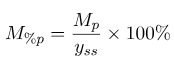
منابع:
Fundamentals of Control Theory by Brian Douglas
C. H. Houpis, S. N. Sheldon, and J. J. D'Azzo, Linear Control System Analysis and Design, 5th ed. Boca Raton, FL: CRC Press, 2013
Y. Bavafa-Toosi, Introduction to Linear Control Systems. Amsterdam, Netherlands: Elsevier, 2017
K. Ogata, Modern Control Engineering, 5th ed. Upper Saddle River, NJ: Pearson, 2010
N. S. Nise, Control Systems Engineering, 6th ed. Hoboken, NJ: John Wiley & Sons, 2011
C.-T. Chen, Linear System Theory and Design, 3rd ed. New York, NY: Oxford University Press, 1999
G. F. Franklin, J. D. Powell, and A. Emami-Naeini, Feedback Control of Dynamic Systems, 7th ed. Boston, MA: Pearson, 2014
#کنترل_خطی #کنترل_مدرن #کنترل_مقاوم #کنترل_فازی #کنترل_کنترل_هوشمند #کنترل_دیجیتال #کنترل_پیش_بین_مبتنی_بر_مدل #کنترل_بهینه #کنترل_چند_متغییره #کنترل_کلاسیک #کنترل_اتوماتیک #کنترل_عصبی #کنترل_چند_عاملی #کنترل_شبکهای #کنترل_تطبیقی #کنترل #کنترل_غیر_خطی #مهندسی_کنترل #متلب #سیمولینک#متلب_سیمولینک #تابع_تبدیل #معادلات_حالت #مدل_سازی #شبیهسازی #کنترل_مبتنی_بر_داده #کنترل_سیستم #سیستم #بهینه_سازی #سنسور #فیدبک #بازخورد