نمایش بسط کسرهای جزئی در متلب
در این مقاله آموزشی، بسط کسرهای جزئی را توضیح میدهیم.
بخش اول
۱. انگیزه
اغلب، در عمل، با مسئله زیر مواجه میشویم. با داشتن یک تابع گویا یا یک تابع تبدیل در مورد سیستمهای کنترل، میخواهیم چنین تابعی را به صورت مجموعی از عبارات سادهتر نمایش دهیم. وقتی چنین عبارات سادهتری را در مورد سیستمهای کنترل داشته باشیم، میتوانیم تبدیل لاپلاس معکوس عبارات سادهتر را برای بدست آوردن پاسخ سیستم در حوزه زمان محاسبه کنیم. میخواهیم تابع را در کسرهای جزئی بسط دهیم.
برای مثال، فرض کنید یک تابع (تبدیل) داریم:
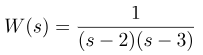
بنابراین هدف ما این است که سعی کنیم این تابع را به صورت زیر نمایش دهیم:
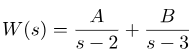
که در آن A و B ثابتهایی هستند که باید تعیین شوند. بسط (2) بسط کسر جزئی نامیده میشود. ابتدا، ما قصد داریم از یک رویکرد در سطح دبیرستان برای حل این مسئله استفاده کنیم. یعنی، از معادله آخر داریم:
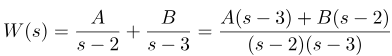
با ضرب عبارات سمت راست آخرین عبارت، به دست میآوریم:
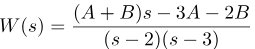
میخواهیم ثابتهای A و B را پیدا کنیم، به طوری که (4) و (1) با هم برابر باشند. این عبارات در صورتی با هم برابرند که معادله زیر برقرار باشد:
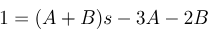
عبارات دو طرف معادلات آخر، چندجملهایهایی در واحد s هستند. این چندجملهایها در صورتی برابرند که ضرایبشان حاصل ضرب جملات با توان یکسان از s، برابر باشند. با استفاده از این منطق، از معادله آخر، سیستم معادلات زیر را به دست میآوریم:
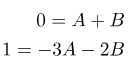
جواب این دستگاه معادلات A=-1 و B=1 است. چگونه میتوان این نتیجه را تأیید کرد؟ میتوانیم به سادگی این مقادیر A و B را در (2) جایگزین کنیم و ببینیم که آیا میتوانیم عبارت اصلی داده شده توسط (1) را بدست آوریم یا خیر. گزینه دیگر استفاده از متلب است. یعنی کد زیر جواب را محاسبه میکند:
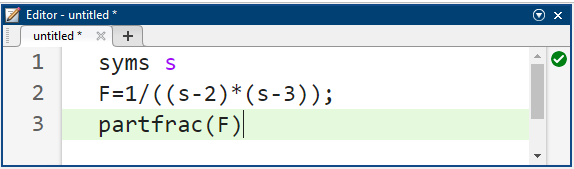
و در نتیجه، به دست میآوریم:
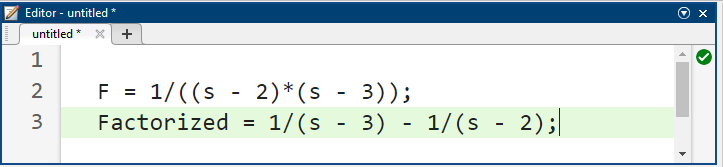
میتوانیم ببینیم که نتیجه ما صحیح است. اجازه دهید به طور خلاصه کد متلب را توضیح دهیم. خط کد "syms s" برای تعریف یک متغیر نمادین s استفاده میشود. وقتی آن متغیر را داشته باشیم، با خط کد ۳ میتوانیم یک عبارت نمادین برای تابع خود تعریف کنیم. در نهایت، خط کد ۵ برای محاسبه بسط استفاده میشود.
نکته: اگرچه رویکرد توضیح داده شده در بالا ممکن است برای توابع پیچیدهتر کار کند، اما اگر جملات زیادی داشته باشیم، خستهکننده و زمانبر میشود. در ادامه، یک رویکرد سیستماتیک و آسان برای استفاده برای محاسبه بسط کسرهای جزئی ارائه میدهیم.
مورد ۱: قطبهای متمایز- (روش پوششی)
ابتدا، اجازه دهید توضیح دهیم که قطبها و صفرهای یک تابع چیستند. یک شکل کلی از یک تابع را در نظر بگیرید.
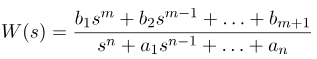
عبارت آخر را میتوان به صورت زیر نوشت:
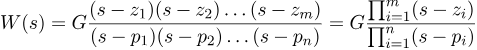
که در آن G یک ثابت است. ثابت zi به عنوان صفر تابع شناخته میشود. ثابت pi به عنوان قطب تابع شناخته میشود. میتوانیم ببینیم که وقتی s=zi باشد، تابع صفر میشود و وقتی s->pi باشد، مقدار تابع به بینهایت میل میکند (برای عدد پی حقیقی). قطبها و صفرها میتوانند حقیقی یا مختلط باشند. حال، با فرض اینکه قطبها متمایز هستند، میتوانیم تابع W(s) را به صورت زیر بنویسیم:
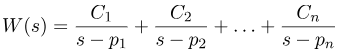
هدف ما توسعه روشی برای محاسبه ثابتهای C1، C2، \ldots و Cn است. آخرین عبارت را در (s-pi) ضرب میکنیم. در نتیجه، داریم:
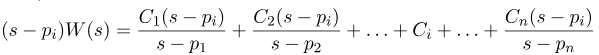
اکنون با جایگذاری s=pi در عبارت (s-pi) W(s)، داریم:
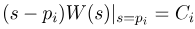
یعنی، ما عبارتی برای محاسبه ثابت Ci به دست آوردهایم. برای محاسبه ثابت Ci مربوط به قطب iام، عبارت بدون فاکتور W(s) را در s-pi ضرب میکنیم و مقدار pi را جایگزین آن میکنیم.
چرا این بسط کسر جزئی مهم است؟ یعنی، پس از محاسبه (9)، میتوانیم به سادگی تبدیل معکوس لاپلاس را با توجه به اینکه:
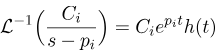
که در آن h(t) یک تابع پلهای هویساید است. میتوانیم این کار را برای همه کسرهای دیگر انجام دهیم تا تبدیل حوزه زمان را بدست آوریم.
بگذارید یک مثال بزنیم.
مثال ۱: پاسخ پله تابع را محاسبه کنید
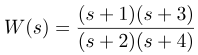
راه حل: پاسخ پله تابع در حوزه مختلط با ضرب تابع تبدیل در عبارت 1/s بدست میآید. این عبارت مربوط به تبدیل لاپلاس تابع پله هویساید است. یعنی، ما میخواهیم تبدیل لاپلاس معکوس زیر را محاسبه کنیم:
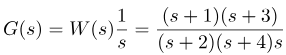
حال بیایید رویکرد توضیح داده شده قبلی را اعمال کنیم. میخواهیم G(s) را به صورت زیر بسط دهیم:
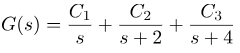
با استفاده از فرمول زیر، به دست میآوریم:
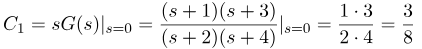
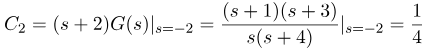
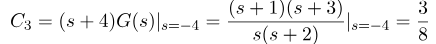
بنابراین عبارت فاکتورگیری شده ما به صورت زیر میشود:
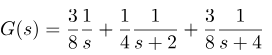
با محاسبه تبدیل لاپلاس معکوس عبارت آخر، به دست میآوریم:
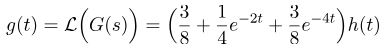
کد متلب زیر برای محاسبه بسط کسرهای جزئی و تبدیل لاپلاس معکوس استفاده شده است.
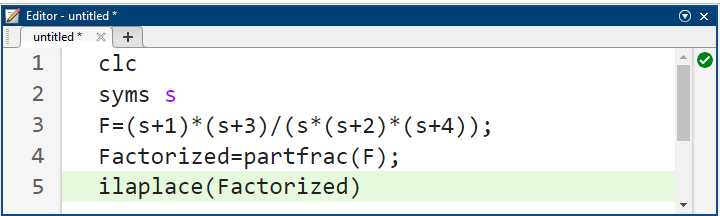
خروجی زیر تولید میشود.

توجه داشته باشید که ما از تابع “( )ilaplace” در متلب برای محاسبه تبدیل معکوس لاپلاس استفاده کردیم.
بخش دوم:
ما با توضیح بسط کسر جزئی ادامه میدهیم. در بخش اول این پست، بسط کسر جزئی را زمانی که تابع گویا (تبدیل) ما ریشههای متمایز دارد، توضیح دادیم. همچنین، مثالی از یک تابع تبدیل با ریشههای حقیقی ارائه دادیم. اکنون اجازه دهید بر روی مثالی از ریشههای متمایز اما پیچیده تمرکز کنیم. چنین مثالهایی اغلب در عمل ظاهر میشوند و باید توجه ویژهای به آنها داشته باشیم.
مثال ۱: پاسخ پله سیستم داده شده توسط یک معادله دیفرانسیل معمولی را محاسبه کنید:
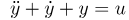
شرایط اولیه را صفر فرض کنید.
راه حل: ما از روش تبدیل لاپلاس برای حل این مسئله استفاده میکنیم. با گرفتن تبدیل لاپلاس از دو طرف معادله بالا، داریم:
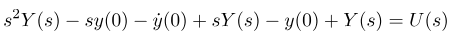
که در آن Y(s) و U(s) تبدیل لاپلاس سیگنالهای حوزه زمان y(t) و u(t) هستند، و y(0) و y(0) شرایط اولیه برای y(t) میباشند. از آنجایی که فرض کردیم شرایط اولیه صفر است، از معادله آخر، به دست میآوریم:
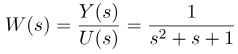
حال، هدف ما محاسبه پاسخ پله سیستم هنگامی است که u(t)=h(t) باشد، که در آن h(t) یک تابع پله Heaviside است. از آنجایی که U(s)=1/s، پاسخ پله در حوزه s به شکل زیر است:
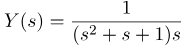
بنابراین، هدف ما محاسبه تبدیل لاپلاس معکوس (معادله بالا) است. حداقل دو راه برای محاسبه این وجود دارد. راه اول استفاده از فرمولی است که در بخش اول این پست توضیح دادیم. ابتدا، قطبها را تعیین میکنیم. قطبها به صورت زیر داده میشوند:
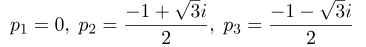
بنابراین عبارت ما برای Y(s) به صورت زیر میشود:
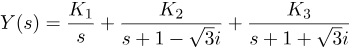
میتوانیم ثابت Ki، i=1,2,3، را با اعمال فرمولی که قبلاً معرفی شد، پیدا کنیم. مشکل این رویکرد این است که باید با اعداد مختلط سر و کار داشته باشیم و این ممکن است خستهکننده باشد. در عوض، یک روش ظریفتر و راحتتر برای حل این مسئله وجود دارد. ایده این است که Y(s) را به صورت زیر نمایش دهیم:
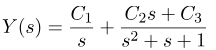
با ضرب عبارت سمت راست معادله آخر، به دست میآوریم:
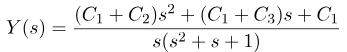
با مقایسه معادله آخر با (4)، به این نتیجه میرسیم که ثابتها باید دستگاه معادلات زیر را ارضا کنند:
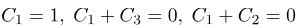
با حل این دستگاه معادلات، به دست میآوریم:
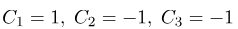
بنابراین میتوانیم بنویسیم:
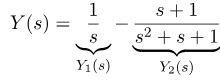
میخواهیم تبدیل معکوس لاپلاس عبارت آخر را محاسبه کنیم. تبدیل معکوس جمله اول آسان است، صرفاً تابع هویساید است. از سوی دیگر، تبدیل معکوس جمله دوم کمی پیچیدهتر است. ایده این است که جمله دوم را به صورت زیر بنویسیم:
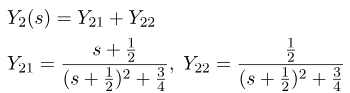
بیایید برخی از ویژگیهای اساسی تبدیل لاپلاس را به یاد بیاوریم. فرض کنید f(t) تابعی در حوزه زمان باشد. بنابراین، تبدیل لاپلاس تابع مقیاسبندی شده f(at) به صورت زیر داده میشود:
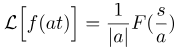
که در آن F(s) تبدیل لاپلاس f(t) است. حال این قانون را برای تبدیل لاپلاس sin(at) اعمال میکنیم. میدانیم که:
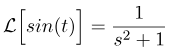
از این عبارت و از (13) نتیجه میشود:
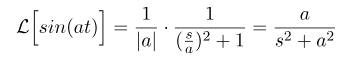
با استفاده از همین اصل، میتوانیم به دست آوریم
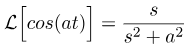
با مقایسه عبارات (15) و (16) با (12)، میتوانیم مشاهده کنیم که این عبارات مشابه هستند، به جز این واقعیت که به جای s، در (12) داریم (s+1/2). برای تکمیل این مثال، باید یکی دیگر از ویژگیهای مهم تبدیل لاپلاس را به یاد بیاوریم. داریم:
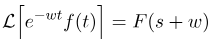
با استفاده از (16) و (17)، به دست میآوریم که تبدیل لاپلاس معکوس Y21 در (12) به صورت زیر است:
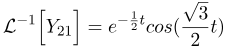
برای محاسبه تبدیل لاپلاس معکوس Y22(s)، Y22(s) را به صورت زیر تبدیل میکنیم:
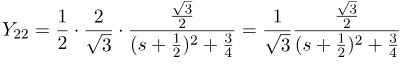
با اعمال (15) و (17) بر (19)، به دست میآوریم:
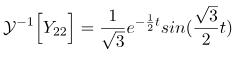
در نهایت، با استفاده از عبارات مشتقشدهی قبلی، به دست میآوریم:
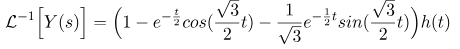
که در آن h(t) تابع هویساید است. کد متلب برای محاسبه تبدیل معکوس لاپلاس در زیر آورده شده است.
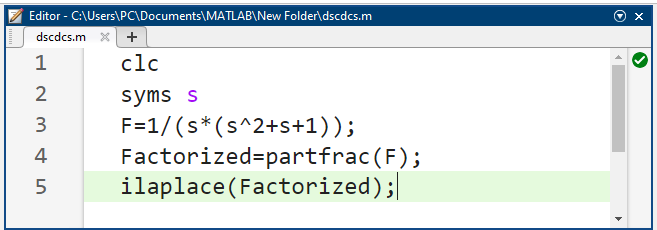
و خروجی این است:

بخش سوم:
این درس به حالتی میپردازد که تابع گویا (تبدیل) قطبهای تکراری دارد (قطبها ریشههای عبارت در مخرج هستند). فرض کنید قطبهای تابع انتقال W(s) برابر با p1، p2، \ldots و p_n باشند. فرض میکنیم قطب p1 سه بار تکرار شده است. سپس، بسط کسر جزئی W(s) به صورت زیر میشود:
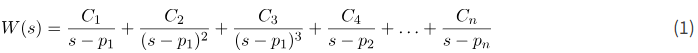
هدف ما یافتن ثابتهای C1، C2، \ldots و Cn است.
اگر آخرین عبارت را در (s-p_{1})^{3} ضرب کنیم، خواهیم داشت:
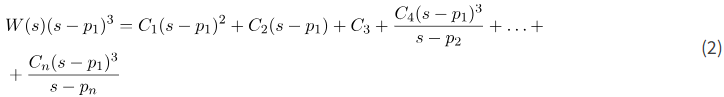
از آخرین معادله، بلافاصله به دست میآوریم

با گرفتن مشتق اول از (2)، داریم:
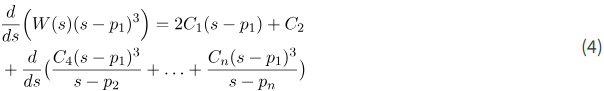
اگر آخرین عبارت را برای s=p1 ارزیابی کنیم، اولین جمله در سمت راست صفر است. همچنین، مشتق عبارت داخل پرانتز به دلیل توان سوم (s-p1) که تمام جملات را در هم ضرب میکند، صفر است. در نتیجه، داریم:

با مشتق گرفتن از (4)، به دست میآوریم
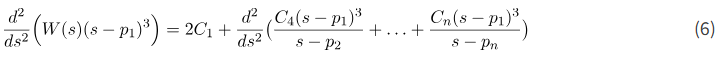
باز هم، جمله دوم در سمت راست عبارت آخر به دلیل ضرب همه جملات در جمله (s-p1)^3 برابر با صفر خواهد بود. از معادله آخر، داریم:

این روش را میتوان زمانی که یک تابع انتقال دارای k قطب تکراری است، تعمیم داد. در این صورت ضرایب به صورت زیر میشوند:
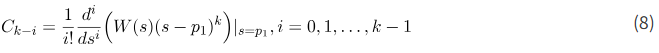
ضرایب باقیمانده مربوط به قطبهای متمایز با استفاده از رویکردهای قبلاً توضیح داده شده که میتوانید بخش اول و دوم بیابید، محاسبه میشوند.
حالا بیایید این مشتقها را با یک مثال توضیح دهیم.
مثال ۱: تبدیل لاپلاس معکوس تابع را بیابید

بسط کسر جزئی به صورت زیر است:
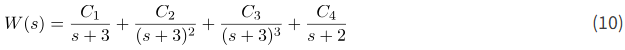
ثابت C3 برابر است با

ثابت C2 برابر است با
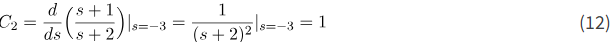
ثابت C1 برابر است با
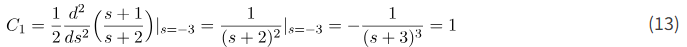
ثابت C4 برابر است با

در نهایت، ما داریم
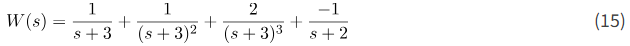
تبدیل معکوس لاپلاس به صورت زیر داده میشود:
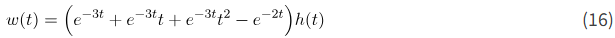
که در آن h(t) تابع پلهای هویساید است.
کد متلب برای حل این مسئله در زیر آمده است
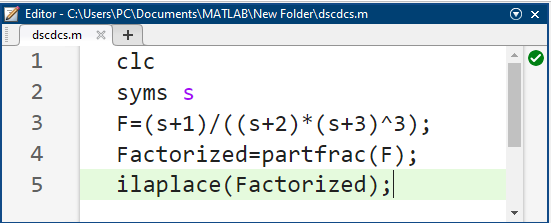
خروجی عبارت است از:

منابع:
Fundamentals of Control Theory by Brian Douglas
C. H. Houpis, S. N. Sheldon, and J. J. D'Azzo, Linear Control System Analysis and Design, 5th ed. Boca Raton, FL: CRC Press, 2013
Y. Bavafa-Toosi, Introduction to Linear Control Systems. Amsterdam, Netherlands: Elsevier, 2017
K. Ogata, Modern Control Engineering, 5th ed. Upper Saddle River, NJ: Pearson, 2010
N. S. Nise, Control Systems Engineering, 6th ed. Hoboken, NJ: John Wiley & Sons, 2011
C.-T. Chen, Linear System Theory and Design, 3rd ed. New York, NY: Oxford University Press, 1999
G. F. Franklin, J. D. Powell, and A. Emami-Naeini, Feedback Control of Dynamic Systems, 7th ed. Boston, MA: Pearson, 2014
#کنترل_خطی #کنترل_مدرن #کنترل_مقاوم #کنترل_فازی #کنترل_کنترل_هوشمند #کنترل_دیجیتال #کنترل_پیش_بین_مبتنی_بر_مدل #کنترل_بهینه #کنترل_چند_متغییره #کنترل_کلاسیک #کنترل_اتوماتیک #کنترل_عصبی #کنترل_چند_عاملی #کنترل_شبکهای #کنترل_تطبیقی #کنترل #کنترل_غیر_خطی #مهندسی_کنترل #متلب #سیمولینک#متلب_سیمولینک #تابع_تبدیل #معادلات_حالت #مدل_سازی #شبیهسازی #کنترل_مبتنی_بر_داده #کنترل_سیستم #سیستم #بهینه_سازی #سنسور #فیدبک #بازخورد