پیادهسازی روش تنظیم کنترل PID با روش زیگلر-نیکولز در متلب
در این مقاله آموزش، ما به طور خلاصه روش تنظیم کنترل PID زیگلر-نیکولز را توضیح میدهیم. به طور دقیقتر، روش دوم را که مبتنی بر افزایش بهره تناسبی تا زمانی که نوسانات پایدار و مداوم در پاسخ رخ دهد، توضیح میدهیم. توضیح دهید که چگونه میتوان مدل سیستم حلقه باز را با روش زیگلر-نیکولز ترکیب کرد تا به سرعت پارامترهای اولیه کنترل PID را طراحی کرد.
هدف، تعیین تجربی پارامترهای کنترلکننده PID است:

که در آن Kp بهره تناسبی، Ti پارامتر عمل انتگرالی و Td پارامتر عمل تناسبی است.
اولین قدم این است که Td=0 و Ti=\infty را تنظیم کنیم (در عمل، این مقدار بسیار بزرگی است). یعنی، ما فقط عمل تناسبی را رها میکنیم. در این صورت، کنترلکننده به صورت زیر است:

فرض کنید دستگاه با P نشان داده شود. در این صورت، نمودار بلوکی سیستم حلقه بسته به صورت زیر خواهد بود.
شکل ۱: سیستم حلقه بسته با بهره تناسبی Kp
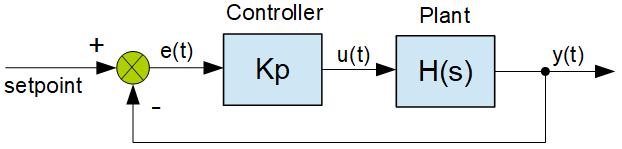
که در آن r ورودی (سیگنال) مرجع و y خروجی سیستم حلقه بسته است.
با فرض اینکه ورودی مرجع اعمال شده r یک ضربه است (در عمل، این میتواند یک پالس کوتاه باشد)، هدف ما یافتن بهره Kp است که نوسانات پایدار و مداوم سیگنال خروجی y را تولید میکند. از صفر شروع میکنیم و Kp را تا زمانی که نوسان پایدار مشاهده شود، افزایش میدهیم. دوره تناوب L چنین نوسان پایداری را میخوانیم. دوره تناوب L نوسانات پایدار، دوره بحرانی یا دوره نهایی نامیده میشود. دوره تناوب L پارامتر ورودی برای طراحی کنترلکننده PID است. فرض کنید Kp^* بهره تناسبی باشد که نوسان پایدار را تولید میکند. بهره تناسبی Kp^* که نوسان پایدار را تولید میکند، بهره بحرانی یا بهره نهایی نامیده میشود.
روش زیگلر-نیکولز پارامترهای کنترلکننده PID را به صورت زیر تعیین میکند:
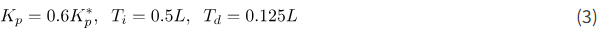
از طرف دیگر، اگر کنترلکننده، کنترلکننده PI باشد، پارامترها عبارتند از

حالا اجازه دهید روش تنظیم را توضیح دهیم. برای توضیح روش تنظیم، فرض میکنیم که گیاه دقیقاً

این مدل برای شبیهسازی پاسخ (برای تولید خروجی) استفاده میشود. با این حال، در طول فرآیند تنظیم، فرض میکنیم که مدل این سیستم را نمیدانیم. ما فقط از خروجی اندازهگیری شده این مدل برای بدست آوردن دادههای پاسخ استفاده میکنیم. فقط بر اساس دادههای پاسخ مشاهده شده، تنظیم کنترلکننده PID را انجام میدهیم.
ما از متلب برای شبیهسازی پاسخ چنین سیستمی استفاده میکنیم.
پاسخ (ضربه) معادله (5) برای Kp=5 در زیر آمده است.
شکل ۲: پاسخ برای Kp=5
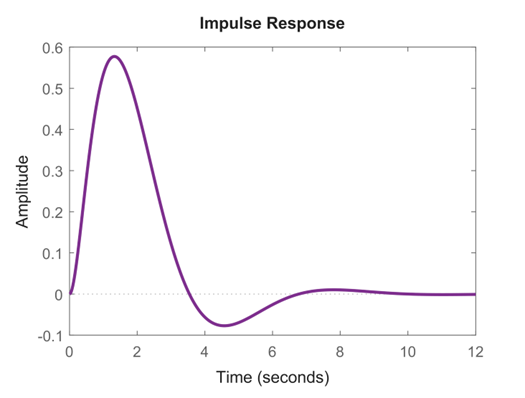
میبینیم که پاسخ ضربه پس از مدتی «از بین میرود». این به دلیل این واقعیت است که دینامیک حلقه بسته به صورت مجانبی پایدار است. پاسخ برای Kp=25 در زیر آورده شده است.
شکل ۳: پاسخ برای Kp=25
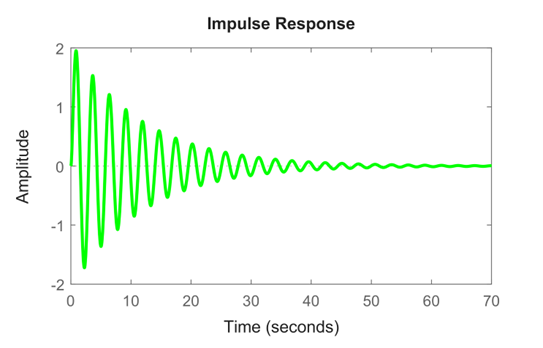
وضعیت در شکل ۳ کمی بهتر است. با این حال، نوسانات هنوز در حال از بین رفتن هستند. در نهایت، پاسخ را برای Kp=30 نشان میدهیم.
شکل ۴: پاسخ برای Kp=30
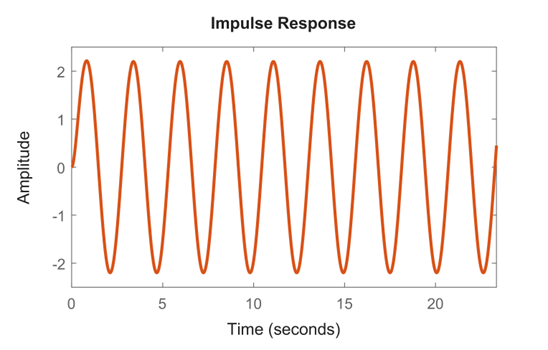
میتوانیم ببینیم که تقریباً برای Kp=30، پاسخ ضربه کاملاً نوسانی میشود و نوسانات پایدار و ماندگار هستند. از طرف دیگر، اگر بهره را بیشتر افزایش دهیم، نوسانات غیرفعال را مشاهده خواهیم کرد.
از روی این نمودار، دوره نوسان را مشاهده میکنیم. دوره نوسان L در شکل زیر نشان داده شده است.
شکل ۵: نوسانات پایدار با دوره تناوب L
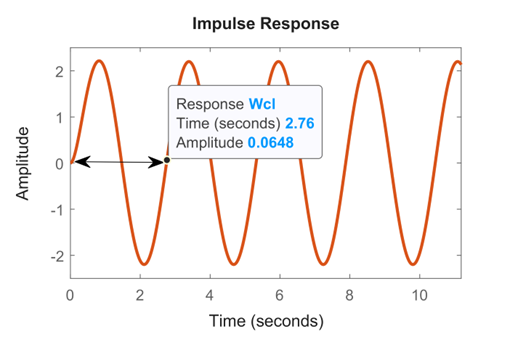
ما دوره نوسان L=2.75 ثانیه را مشاهده میکنیم. این پارامتر ورودی اصلی برای طراحی کنترلکننده PID است.
با استفاده از روش زیگلر-نیکولز، پارامترهای زیر را بدست میآوریم:

میتوانیم کنترلکننده PID (1) را به صورت زیر بنویسیم:

با جایگزینی (6) در (7)، به دست میآوریم:

ما پاسخ پله سیستم حلقه بسته به دست آمده با استفاده از (8) را شبیهسازی میکنیم. نتایج در شکل زیر نشان داده شده است.
شکل ۶: پاسخ پله سیستم حلقه بسته
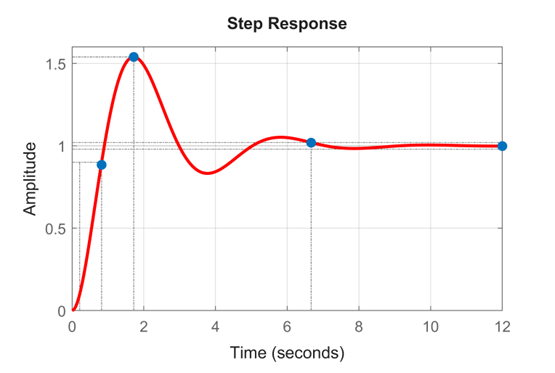
میتوانیم مشاهده کنیم که سیستم حلقه بسته دارای خطای حالت ماندگار صفر است. با این حال، اضافه جهش بسیار بزرگی دارد. میتوانیم با تنظیم دقیق کنترلر PID، اضافه جهش را کاهش دهیم. میتوانیم با افزایش عمل مشتقگیری، اضافه جهش را کاهش دهیم. این کار اضافه جهش را کاهش میدهد و همزمان سرعت پاسخ را نیز کاهش میدهد. برای افزایش سرعت پاسخ، بهره انتگرال را افزایش میدهیم. ضرایب جدید عبارتند از:

کنترلکننده اصلاحشده عبارت است از

شکل زیر پاسخ حلقه بسته کنترل کننده PID اصلی (کنترل کننده PID زیگلر-نیکولز) را با کنترل کننده PID اصلاح شده (کنترل کننده PID اصلاح شده) مقایسه می کند.
شکل ۷: پاسخ پله حلقه بسته کنترلکنندههای PID اولیه و اصلاحشده
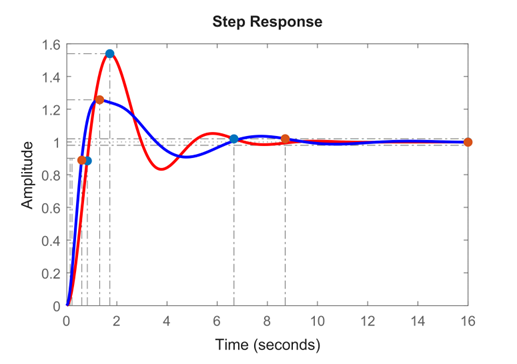
از شکل 7، میتوانیم مشاهده کنیم که در مقایسه با کنترلر PID زیگلر-نیکولز اولیه، فراجهش کاهش یافته و زمان خیزش بهبود یافته است. کدهای MATLAB مورد استفاده برای تولید نمودارها در زیر آورده شده است.
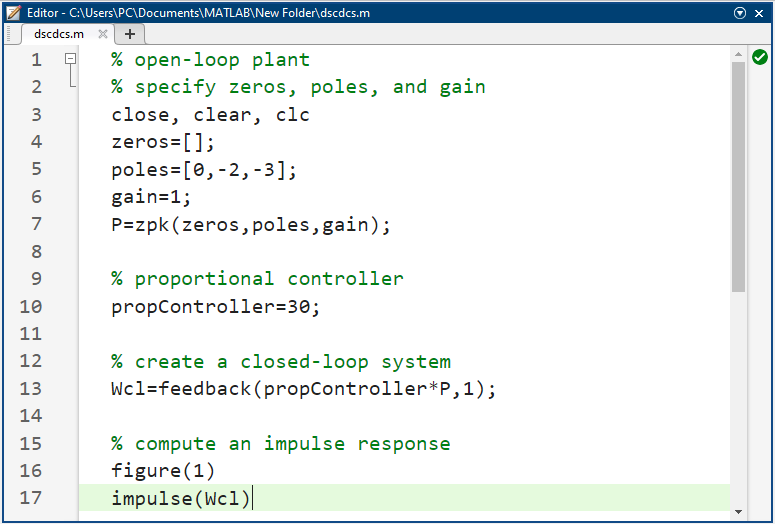
کدهای متلب:
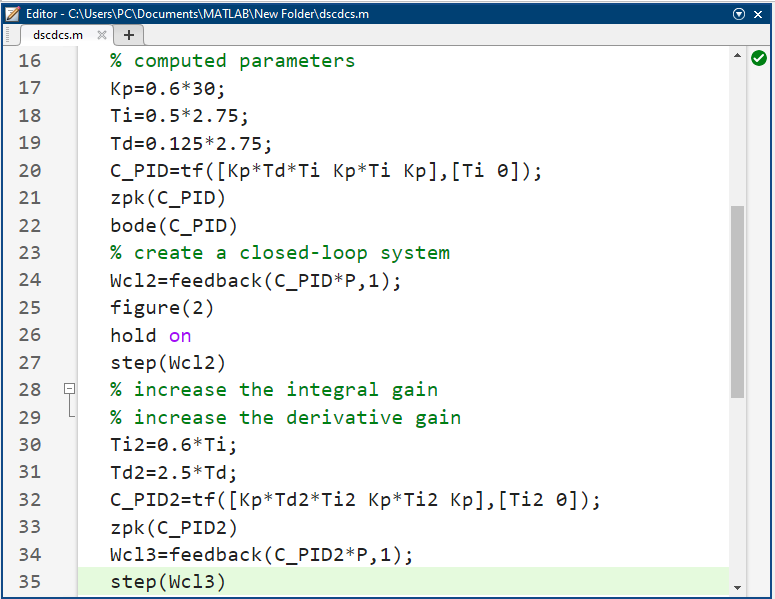
ادامه کدهای متلب:
منابع:
Fundamentals of Control Theory by Brian Douglas
C. H. Houpis, S. N. Sheldon, and J. J. D'Azzo, Linear Control System Analysis and Design, 5th ed. Boca Raton, FL: CRC Press, 2013
Y. Bavafa-Toosi, Introduction to Linear Control Systems. Amsterdam, Netherlands: Elsevier, 2017
K. Ogata, Modern Control Engineering, 5th ed. Upper Saddle River, NJ: Pearson, 2010
N. S. Nise, Control Systems Engineering, 6th ed. Hoboken, NJ: John Wiley & Sons, 2011
C.-T. Chen, Linear System Theory and Design, 3rd ed. New York, NY: Oxford University Press, 1999
G. F. Franklin, J. D. Powell, and A. Emami-Naeini, Feedback Control of Dynamic Systems, 7th ed. Boston, MA: Pearson, 2014
#کنترل_خطی #کنترل_مدرن #کنترل_مقاوم #کنترل_فازی #کنترل_کنترل_هوشمند #کنترل_دیجیتال #کنترل_پیش_بین_مبتنی_بر_مدل #کنترل_بهینه #کنترل_چند_متغییره #کنترل_کلاسیک #کنترل_اتوماتیک #کنترل_عصبی #کنترل_چند_عاملی #کنترل_شبکهای #کنترل_تطبیقی #کنترل #کنترل_غیر_خطی #مهندسی_کنترل #متلب #سیمولینک#متلب_سیمولینک #تابع_تبدیل #معادلات_حالت #مدل_سازی #شبیهسازی #کنترل_مبتنی_بر_داده #کنترل_سیستم #سیستم #بهینه_سازی #سنسور #فیدبک #بازخورد