نمایش فرمهای درجه دوم، ماتریسهای معین مثبت، معین منفی و نیمه معین در متلب
خلاصه مطالب:
این مقاله درباره نمایش فرمهای درجه دوم، ماتریسهای معین مثبت، معین منفی و نیمه معین در متلب است. غلاو بر این در این مقاله به توضیح رابطه بین فرمهای درجه دوم و ماتریسهای معین و نیمه معین میپردازد. همچنین، تستهایی را برای تعیین اینکه آیا یک ماتریس مثبت (نیمه) معین، منفی (نیمه) معین یا نامعین است، ارائه میدهد. مقاله نحوه بصریسازی فرمهای درجه دوم در متلب را توضیح میدهد و مفهوم مینورهای اصلی ماتریسها را مورد بحث قرار میدهد. این مقاله همچنین شرایطی را که یک ماتریس برای معین منفی، نیمه معین منفی، نیمه معین مثبت و نامعین بودن باید داشته باشد، پوشش میدهد.
سرفصل مطالب:
در این مقاله آموزشی مباحث زیر را توضیح میدهیم:
1) فرمهای درجه دوم. ارتباط بین فرمهای درجه دوم ماتریسهای معین و نیمه معین
2) ماتریسهای معین. آزمونهایی برای تعیین اینکه آیا یک ماتریس مثبت (نیمه) معین، منفی (نیمه) معین یا نامعین است
3) رسم فرمهای درجه دوم در متلب
4) مینورهای اصلی پیشرو ماتریسها
تابع زیر را در نظر میگیریم:
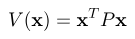
که در آن یک ماتریس متقارن است، یعنی P=P^{T}. این تابع نشان دهنده یک فرم درجه دوم است که به صورت یک ماتریس فشرده نوشته شده است. تابع V(\mathbf{x})، که در آن \mathbf{x}\in \mathbb{R}^{2} برای چندین فرم مختلف ماتریس P (که در معادله (7) داده شده است)، در شکلهای 1-5 زیر نشان داده شده است. به عنوان مثال، این تابع را در نظر بگیرید:
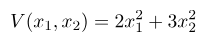
که در آن x1 و x2 متغیرهای حقیقی هستند. این تابع در واقع یک فرم درجه دوم است زیرا
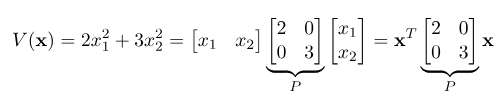
که
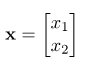
برای نشان دادن بهتر ساختار فرمهای درجه دوم، یک مورد دوبعدی زیر را در نظر میگیریم.
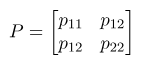
و در نتیجه، تابع اصلی ما به شکل زیر در میآید
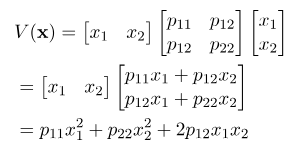
بیایید این توابع را برای چندین مقدار از ماتریس P تجسم کنیم. پنج ماتریس P زیر را در نظر بگیرید
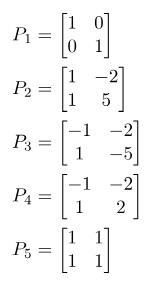
تابع V(x) برای این پنج حالت در شکلهای ۱ تا ۵ زیر نشان داده شده است.
شکل 1: ماتریس ….: نمایش تابع V(x) برای ماتریس P1
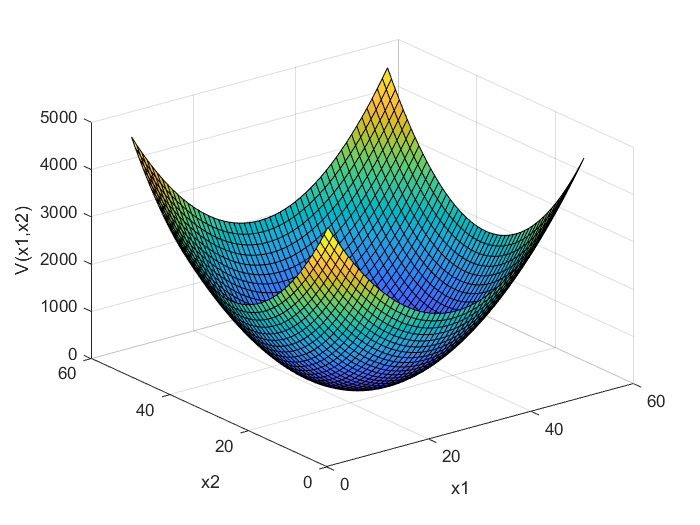
شکل 2: ماتریس ….: نمایش تابع V(x) برای ماتریس P2
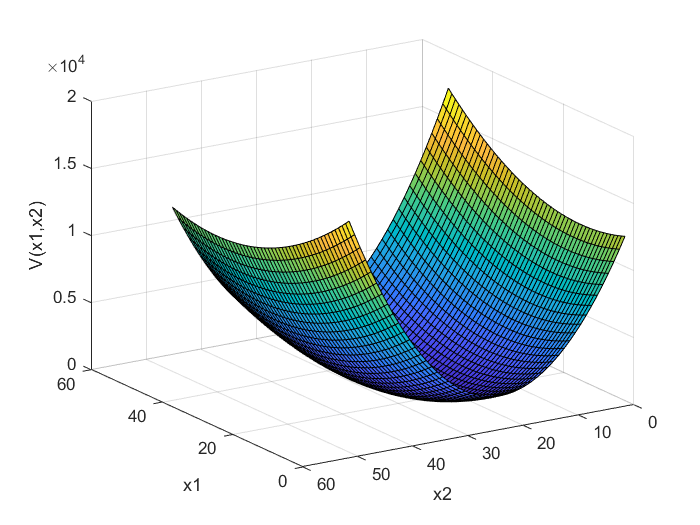
شکل 3: ماتریس منفی معین (Negative definite): نمایش تابع V(x) برای ماتریس P3
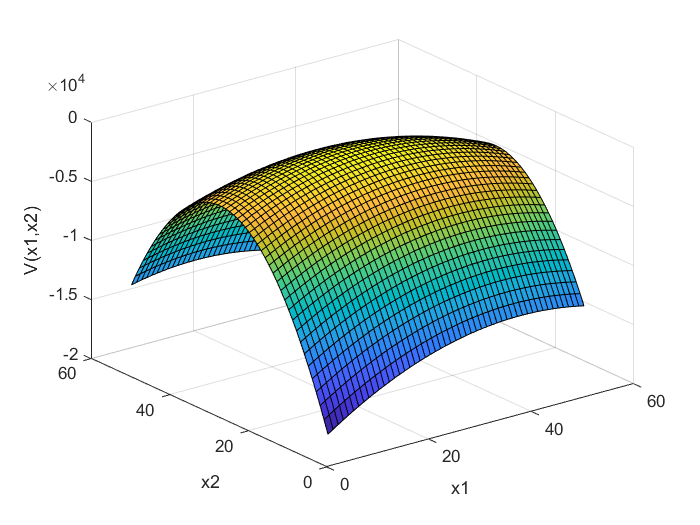
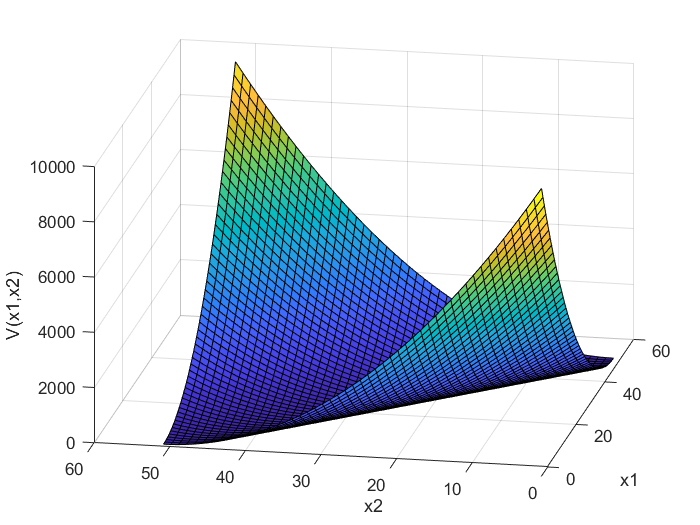
شکل 4: ماتریس نامعین (Indefinite): نمایش تابع V(x) برای ماتریس P4
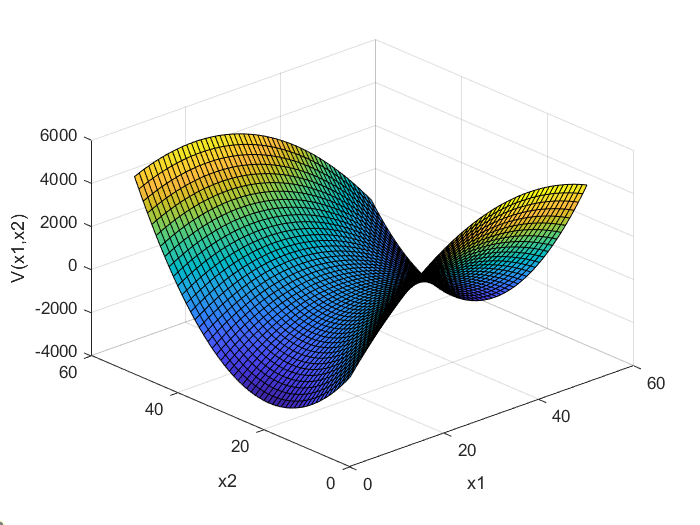
شکل ۵: ماتریس نیمه معین مثبت (Positive Semi-definite): نمایش تابع V(x) برای ماتریس P5
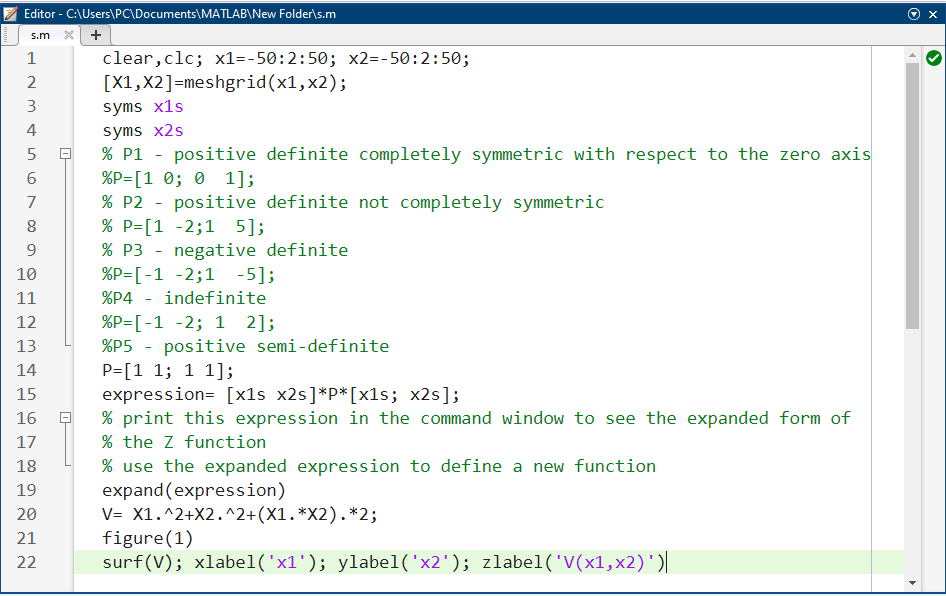
کد متلب مورد استفاده برای تولید این نمودارها در شکل زیر آمده است.
کد متلب:
در اینجا، باید به یک نکته مهم در مورد فرمهای درجه دوم اشاره کنیم. توجه داشته باشید که در تعریف فرم درجه دوم، که توسط معادله (1) ارائه شده است، فرض بر این است که ماتریس P متقارن است. با این حال، بسیاری از ماتریسها متقارن نیستند. آیا میتوان فرمهای درجه دوم را برای چنین ماتریسهایی تعریف کرد؟ پاسخ مثبت است، زیرا
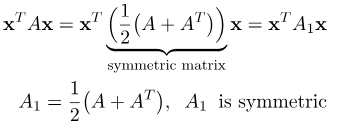
در نتیجه، هر ماتریس غیرمتقارن، یک فرم درجه دوم با یک ماتریس متقارن تعریف میکند. یعنی، برای هر ماتریس غیرمتقارن، میتوانیم یک فرم درجه دوم با یک ماتریس متقارن پیدا کنیم.
از معادله (6)، میتوانیم ببینیم که تابع V(x) درجه دوم است. برای اینکه این تابع مثبت معین باشد، ماتریس P باید یک ماتریس مثبت معین باشد. ماتریس حقیقی متقارن P را ماتریس مثبت معین مینامیم اگر و تنها اگر شرط زیر برقرار باشد.
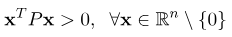
فرمهای درجه دوم مثبت-معین مربوط به ماتریسهای مثبت معین P1 و P2 در شکلهای 1 و 2 نشان داده شدهاند. اکنون اجازه دهید در مورد آزمونی برای آزمایش مثبت بودن معین بودن یک ماتریس بحث کنیم. حالت دوبعدی ارائه شده توسط معادله (6) را در نظر میگیریم. از این معادله، داریم:
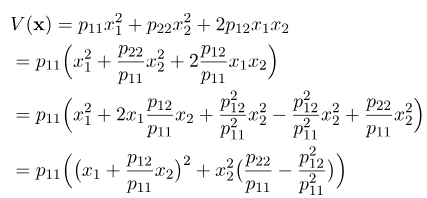
بیایید آخرین عبارت را تحلیل کنیم. فرض کنیم p11 مثبت است. سپس، به راحتی میتوان دید که عبارت اول برای هر x1 و x2 متفاوت از صفر، مثبت است، یعنی
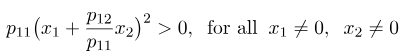
بیایید اصطلاح دوم را بررسی کنیم
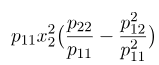
عبارت دوم برای همه ![]() مثبت است اگر
مثبت است اگر
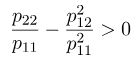
معادله آخر معادل است با
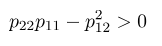
به طور خلاصه، فرم درجه دوم (6) مثبت معین است اگر
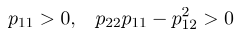
از طرف دیگر، دوباره ماتریس اصلی P را در نظر بگیرید
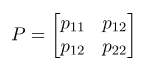
عدد p_{11} مینور اصلی پیشرو از مرتبه 1 (یا به طور خلاصه، مینور اصلی پیشرو مرتبه اول) ماتریس P است و عبارت p_{22}p_{11}-p_{12}^{2} مینور اصلی پیشرو از مرتبه 2 (یا به طور خلاصه، مینور اصلی پیشرو مرتبه دوم) ماتریس P است. مینورهای اصلی پیشرو از مرتبه خاص، دترمینانهای زیرماتریسهای بالا-چپ ماتریس هستند. به طور کلی، میتوان گفت که مینور اصلی پیشرو از مرتبه k، دترمینان ماتریسی است که با پاک کردن n-k ستون و n-k سطر آخر ماتریس P\in \mathbb{R}^{n\times n} به دست میآید. بنابراین، ماتریس مرتبه دوم P مثبت معین است اگر و تنها اگر، مینورهای اصلی پیشرو مرتبه اول و مرتبه دوم آن مثبت باشند.
با استفاده از این آزمون، میتوانیم مشخص کنیم که ماتریسهای P1 و P2 تعریف شده در (7) مثبت هستند. در نتیجه، فرمهای درجه دوم مربوطه که در شکل 1 و شکل 2 نشان داده شدهاند، مثبت قطعی هستند.
شرط مثبت بودن قطعی:
به طور کلی، ماتریس n بعدی P\in \mathbb{R}^{n\times n}:

مثبت معین است اگر و تنها اگر:
- 1 1 )مینور اصلی پیشرو مرتبه اول مثبت است، یعنی دترمینان گوشه بالا سمت چپ ۱ در ۱ از P مثبت است:
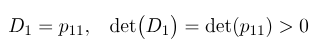
- 2) مینور اصلی پیشرو مرتبه دوم مثبت است، یعنی دترمینان گوشه بالا سمت چپ ۲ در ۲ از P مثبت است:
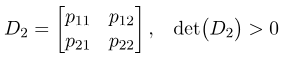
3) مینور اصلی پیشرو مرتبه سوم مثبت است، یعنی دترمینان گوشه بالا سمت چپ ۳ در ۳ از P مثبت است:

4) دترمینان ماتریس P مثبت است (این مینور اصلی پیشرو مرتبه n است)
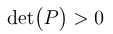
این شرط سیلوستر برای آزمایش قطعی بودن مثبت یک ماتریس است.
این آزمون را روی ماتریس زیر اعمال میکنیم
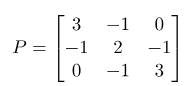
ما داریم
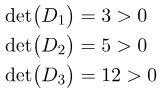
در نتیجه، ماتریس P مثبت-معین است.
اکنون تعاریف ماتریسهای منفی معین، منفی نیمه معین، مثبت نیمه معین و نامعین را بیان میکنیم.
ماتریس معین منفی: ماتریس P منفی معین است اگر و تنها اگر
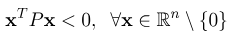
ماتریس نیمه معین منفی: ماتریس P منفی معین است اگر و تنها اگر
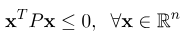
ماتریس نیمه معین مثبت: ماتریس P منفی معین است اگر و تنها اگر
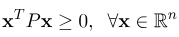
ماتریس نامعین: یک ماتریس P نامعین است اگر و تنها اگر برای برخی از ∈x∈P∈>0 و برای برخی از ∈x∈P∈<0 باشد.
ماتریس P_{3} در (7) منفی معین و ماتریس P_{4} نامعین است. فرم درجه دوم تعریف شده برای ماتریس منفی معین P_{3} در شکل 3 نشان داده شده است، در حالی که فرم درجه دوم تعریف شده برای ماتریس نامعین P_{4} در شکل 4 نشان داده شده است. ماتریس P_{5} در (7) مثبت نیمه معین است. فرم درجه دوم تعریف شده برای این ماتریس در شکل 5 نشان داده شده است. فرم درجه دوم برای ماتریس P_{5} به صورت زیر است
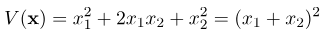
میبینیم که این فرم درجه دوم، مثبت-نیمه-قطعی است، زیرا برای x_{1}=-x_{2}، فرم درجه دوم صفر است و در غیر این صورت مثبت است (به جز در (0,0)). یعنی، نقطهای (x_{1},x_{2}) وجود دارد که با (0,0) متفاوت است و این فرم درجه دوم برای آن صفر است. در مرحله بعد، آزمونهایی برای منفی-قطعی، نیمه-قطعی و نامعین بودن بیان میکنیم.
شرط منفی بودن معین: ماتریس P در (17) منفی معین است اگر و تنها اگر:
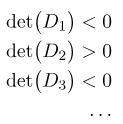
یعنی، ماتریس P منفی معین است اگر و تنها اگر مینورهای اصلی مقدم آن، علامتشان را با شروع از مینور مرتبه اول که باید منفی باشد، متناوباً تغییر دهند. یا به عبارت دیگر، ماتریس P منفی معین است اگر و تنها اگر مینورهای اصلی مقدم آن از درجه فرد منفی و مینورهای اصلی مقدم از درجه زوج مثبت باشند.
شرط نامعین بودن: یک ماتریس P نامعین است اگر و تنها اگر یکی از مینورهای اصلی مقدم غیر صفر باشد، اما علامت آن از الگوی ماتریسهای معین مثبت یا معین منفی پیروی نکند.
شرایط نیمه معین بودن مثبت و منفی با شرایط معین بودن مطلق مثبت و منفی متفاوت است، زیرا آنها شامل همه مینورهای اصلی و نه فقط مینورهای اصلی پیشرو هستند. مینورهای اصلی به سادگی با پاک کردن ستونها و ردیفهای خاصی از یک ماتریس و محاسبه دترمینان به دست میآیند. در اینجا، فرآیند پاک کردن ستونها و ردیفها فقط به ردیفها و ستونهای آخر مانند مورد مینورهای اصلی پیشرو محدود نمیشود. شماره ستون و ردیف باید یکسان باشد. یعنی، شاخصهای ردیفهای حذف شده باید برابر با شاخصهای ستونهای حذف شده باشند. به عنوان مثال، ماتریس 3×3 P را در نظر بگیرید:
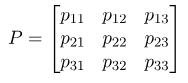
ریزمعیارهای اصلی مرتبه دوم آن عبارتند از
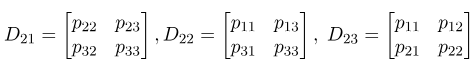
شرط نیمه معین مثبت: یک ماتریس P نیمه معین مثبت است اگر و تنها اگر همه مینورهای اصلی آن \ge 0 باشند.
شرط نیمه معین منفی: یک ماتریس P نیمه معین منفی است اگر و تنها اگر مینورهای اصلی آن از درجه فرد \le 0 و مینورهای اصلی آن از درجه زوج \ge 0 باشند.
منابع:
Fundamentals of Control Theory by Brian Douglas
C. H. Houpis, S. N. Sheldon, and J. J. D'Azzo, Linear Control System Analysis and Design, 5th ed. Boca Raton, FL: CRC Press, 2013
Y. Bavafa-Toosi, Introduction to Linear Control Systems. Amsterdam, Netherlands: Elsevier, 2017
K. Ogata, Modern Control Engineering, 5th ed. Upper Saddle River, NJ: Pearson, 2010
N. S. Nise, Control Systems Engineering, 6th ed. Hoboken, NJ: John Wiley & Sons, 2011
C.-T. Chen, Linear System Theory and Design, 3rd ed. New York, NY: Oxford University Press, 1999
G. F. Franklin, J. D. Powell, and A. Emami-Naeini, Feedback Control of Dynamic Systems, 7th ed. Boston, MA: Pearson, 2014
#کنترل_خطی #کنترل_مدرن #کنترل_مقاوم #کنترل_فازی #کنترل_کنترل_هوشمند #کنترل_دیجیتال #کنترل_پیش_بین_مبتنی_بر_مدل #کنترل_بهینه #کنترل_چند_متغییره #کنترل_کلاسیک #کنترل_اتوماتیک #کنترل_عصبی #کنترل_چند_عاملی #کنترل_شبکهای #کنترل_تطبیقی #کنترل #کنترل_غیر_خطی #مهندسی_کنترل #متلب #سیمولینک#متلب_سیمولینک #تابع_تبدیل #معادلات_حالت #مدل_سازی #شبیهسازی #کنترل_مبتنی_بر_داده #کنترل_سیستم #سیستم #بهینه_سازی #سنسور #فیدبک #بازخورد