شبیهسازی سیستمهای کنترل با محدودیتهای عملگر در سیمولینک
در این مقاله آموزشی نحوه شبیهسازی یک سیستم کنترل با محدودیتهای عملگر در متلب-سیمولینک را توضیح میدهیم.
مدل سیمولینک در زیر آورده شده است.
شکل ۱: مدل سیمولینک سیستم حلقه بسته.
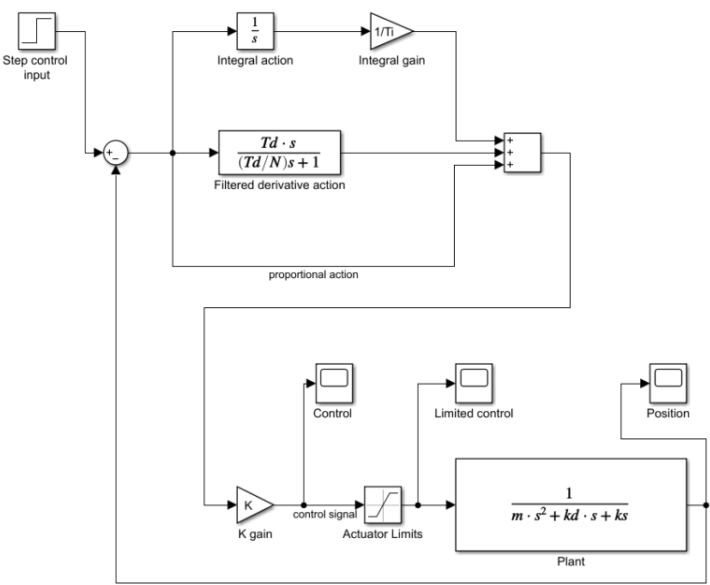
این نمودار بلوکی سیمولینک، الگوریتم کنترل PID را به شکل زیر شبیهسازی میکند.
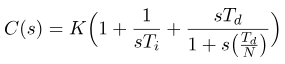
که در آن
C(s) تابع تبدیل کنترلر است.
K، Ti، Td، N - ثابتهای کنترلر هستند که به عنوان پارامترهای تنظیم استفاده میشوند.
s تبدیل لاپلاس است.
این شکل از کنترلکننده PID مبتنی بر جایگزینی عبارت مشتق ایدهآل Tds s با نسخه فیلتر شده آن است.
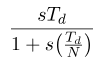
این عمل مشتق فیلتر شده برای سیگنالهای فرکانس پایین به عنوان یک مشتق عمل میکند، در حالی که برای سیگنالهای فرکانس بالا به عنوان یک فیلتر پایین گذر عمل میکند. به این ترتیب، میتوانیم از تقویت اجزای سیگنال فرکانس بالا توسط عمل مشتق خالص جلوگیری کنیم.
حالت طرح، یک سیستم جرم-فنر-میراگر است که با معادله دیفرانسیل زیر توصیف میشود:
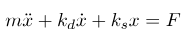
که در آن
m جرم
kd ثابت میرایی
ks ثابت فنر
F نیروی اعمال شده است
تابع تبدیل مربوط به این مدل به صورت زیر داده شده است:
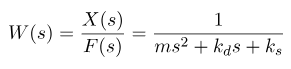
در واقعیت، محرکهای کنترلی نمیتوانند نیروی بینهایت اعمال کنند. برای در نظر گرفتن این محدودیت، محدودیتهای محرک را به مدل سیستم اضافه میکنیم. محدودیتهای محرک در شکل 1 نشان داده شده است.
هدف این آموزش توضیح نحوه تنظیم کنترلکنندههای PID نیست. در عوض، ما عمدتاً بر توضیح نحوه شبیهسازی رفتار سیستم تمرکز میکنیم. ما رفتار سیستم را برای پارامترهای زیر شبیهسازی میکنیم:
m=30، kd=5، ks=10، Ti=20، Td=0.1، N=10 و K=1000 را در نظر میگیریم و محدودیتهای محرک را روی -100 و 100 قرار میدهیم. همچنین، سیگنال ورودی پله برابر با 1 است.
خروجی سیستم حلقه بسته در شکل زیر نشان داده شده است. این نمودار با استفاده از پروب «موقعیت» در نمودار سیمولینک بدست آمده است.
شکل ۱: پاسخ سیستم حلقه بسته
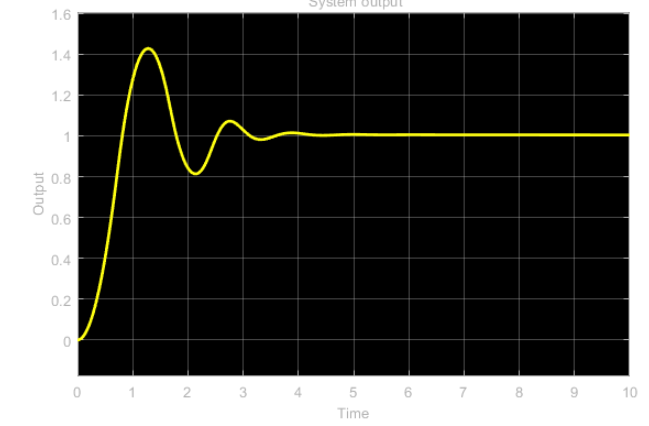
سیگنال کنترلی که خروجی مستقیم الگوریتم کنترل است در شکل زیر نشان داده شده است. این سیگنال با استفاده از پروب «کنترل» در نمودار سیمولینک بدست میآید.
سیگنال کنترلی که خروجی مستقیم الگوریتم کنترل است در شکل زیر نشان داده شده است. این سیگنال با استفاده از پروب «کنترل» در نمودار سیمولینک بدست میآید.
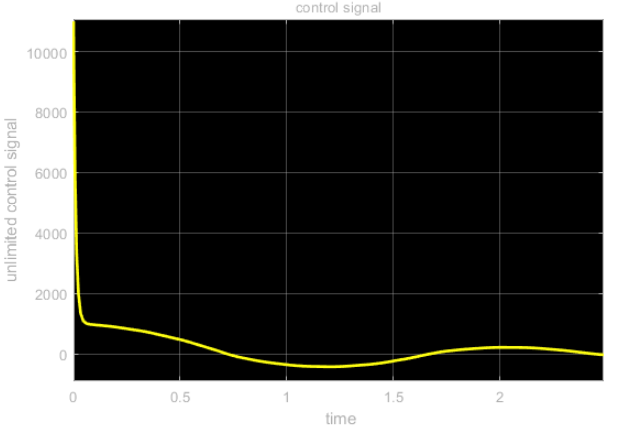
میتوانیم ببینیم که این خروجی مقادیر بزرگی دارد. با این حال، در عمل، نمیتوانیم به این مقادیر بزرگ دست یابیم. این مقادیر از طریق فیلتر محدودکنندهی محرک فیلتر میشوند. سیگنال محدودی که به سیستم اعمال میشود در شکل زیر نشان داده شده است. توجه داشته باشید که این سیگنال توسط پروب «کنترل محدود» به دست میآید.
شکل ۳: سیگنال کنترل محدود.
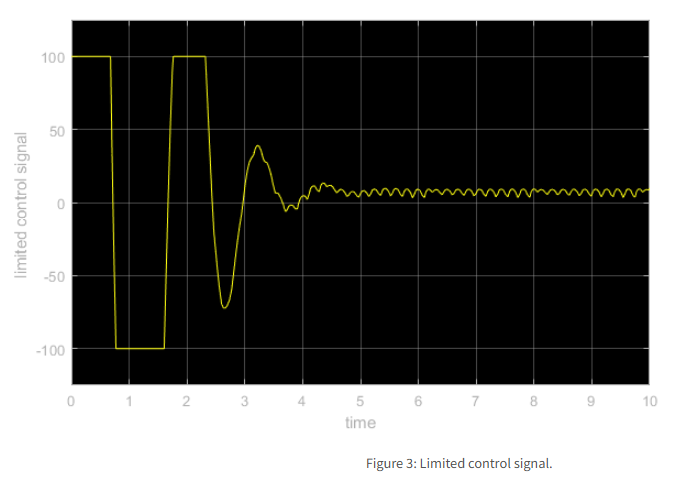
از شکل ۳، میتوانیم اثر اشباع محرک را مشاهده کنیم.
منابع:
Fundamentals of Control Theory by Brian Douglas
C. H. Houpis, S. N. Sheldon, and J. J. D'Azzo, Linear Control System Analysis and Design, 5th ed. Boca Raton, FL: CRC Press, 2013
Y. Bavafa-Toosi, Introduction to Linear Control Systems. Amsterdam, Netherlands: Elsevier, 2017
K. Ogata, Modern Control Engineering, 5th ed. Upper Saddle River, NJ: Pearson, 2010
N. S. Nise, Control Systems Engineering, 6th ed. Hoboken, NJ: John Wiley & Sons, 2011
C.-T. Chen, Linear System Theory and Design, 3rd ed. New York, NY: Oxford University Press, 1999
G. F. Franklin, J. D. Powell, and A. Emami-Naeini, Feedback Control of Dynamic Systems, 7th ed. Boston, MA: Pearson, 2014
#کنترل_خطی #کنترل_مدرن #کنترل_مقاوم #کنترل_فازی #کنترل_کنترل_هوشمند #کنترل_دیجیتال #کنترل_پیش_بین_مبتنی_بر_مدل #کنترل_بهینه #کنترل_چند_متغییره #کنترل_کلاسیک #کنترل_اتوماتیک #کنترل_عصبی #کنترل_چند_عاملی #کنترل_شبکهای #کنترل_تطبیقی #کنترل #کنترل_غیر_خطی #مهندسی_کنترل #متلب #سیمولینک#متلب_سیمولینک #تابع_تبدیل #معادلات_حالت #مدل_سازی #شبیهسازی #کنترل_مبتنی_بر_داده #کنترل_سیستم #سیستم #بهینه_سازی #سنسور #فیدبک #بازخورد