■ تبدیل مدلهای فضای حالت به تابع تبدیل در متلب
در این مقاله آموزشی و در آموزش ویدیویی همراه، نحوه تبدیل مدلهای فضای حالت به توابع انتقال را توضیح میدهیم. نحوه انجام این تبدیل را به صورت تحلیلی و در متلب توضیح میدهیم.
مدل فضای حالت زیر را در نظر بگیرید

که در آن \mathbf{x}\in \mathbb{R}^{n} بردار حالت، \mathbf{u}\in \mathbb{R}^{m} بردار ورودی و \mathbf{y}\in \mathbb{R}^{r} بردار ورودی است، ماتریسهای A\in \mathbb{R}^{n\times n}، B\in \mathbb{R}^{n\times m}، C\in \mathbb{R}^{r\times n} و D\in \mathbb{R}^{r\times m} ماتریسهای سیستم هستند.
هدف ما تبدیل این مدل فضای حالت به یک تابع انتقال (که به دلیل وجود چندین ورودی و خروجی در سیستم، ماتریس انتقال نیز نامیده میشود) است: تابع انتقال به شکل زیر خواهد بود:

که در آن W(s)\in \mathbb{C}^{r \times m} تابع تبدیل و s\in \mathbb{C} متغیر مختلط (به دست آمده با اعمال تبدیل لاپلاس) است، و Y(s)\in \mathbb{C}^{r} و U(s)\in \mathbb{C}^{r} تبدیلهای لاپلاس بردارهای خروجی و ورودی هستند. توجه داشته باشید که تبدیلهای لاپلاس بردار با حروف بزرگ نشان داده میشوند.
تبدیل لاپلاس را به سیستم اصلی (1) خود اعمال میکنیم. از آنجایی که توابع تبدیل برای شرایط اولیه صفر تعریف شدهاند، باید این واقعیت را هنگام اعمال تبدیل لاپلاس در نظر بگیریم. در نتیجه، از (1)، داریم:

که در آن X(s) تبدیل لاپلاس بردار حالت است. از معادله اول داریم:

که در آن I \in \mathbb{R}^{n\times n} ماتریس همانی است. از این معادله، داریم

که در آن ∈(sI-A)∈^{-1} معکوس ∈(sI-A)∈ است. با جایگزینی (5) در معادله خروجی (3)، داریم:
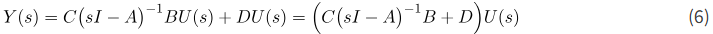
معادله آخر را میتوان به صورت فشرده نوشت

که در آن W(s) تابع تبدیل است

در مورد سیستمهای تک ورودی-تک خروجی، تابع تبدیل ماتریسی نیست و میتوانیم بنویسیم

مثال: تابع تبدیل سیستم زیر را بیابید؟
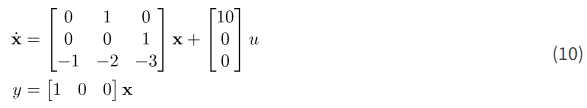
راه حل:
ابتدا، (sI-A) را محاسبه میکنیم. داریم
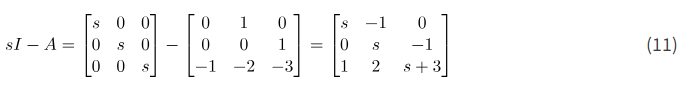
ماتریس معکوس \big(sI-A\big)^{-1} به صورت زیر تعریف میشود:

که در آن \text{adj}\big(sI-A\big) ماتریس کمکی \big(sI-A\big) و \text{det}\big(sI-A\big) ماتریس دترمینان \big(sI-A\big) است. ماتریس کمکی با ترانهاده کردن ماتریس کوفاکتور تشکیل میشود. ماتریس کوفاکتور \big(sI-A\big) به صورت زیر است
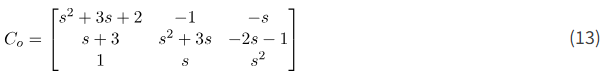
در نتیجه، ماتریس الحاقی به صورت زیر است:
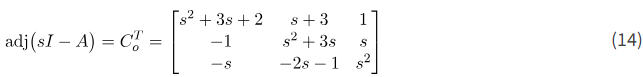
دترمینان ماتریس \big(sI-A\big) برابر است با \text{det}\big(sI-A\big)=s^3+3s^2+2s+1
در نهایت، ماتریس تابع انتقال ما به صورت زیر است:
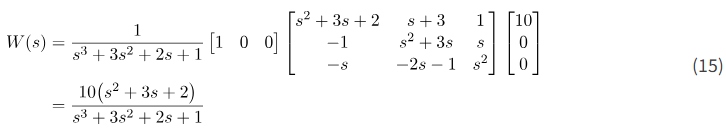
در زیر کدهای متلب برای محاسبه تابع تبدیل آمده است. دو رویکرد وجود دارد. در اینجا رویکرد اول که به جعبه ابزار نمادین متلب متکی است، آمده است.

دستور syms برای تعریف یک متغیر مختلط نمادین s استفاده میشود. سایر بخشهای کد نیازی به توضیح ندارند.
رویکرد دوم در زیر ارائه شده است. این رویکرد به جعبه ابزار سیستم کنترل متلب متکی است.

ما مدل فضای حالت را با استفاده از تابع ( )ss در متلب تعریف میکنیم. سپس چنین مدل فضای حالت را با استفاده از دستور ( )tf به فرم تابع انتقال تبدیل میکنیم.
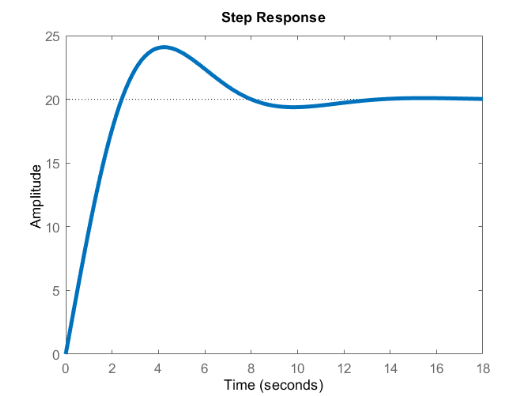
در زیر پاسخ پله سیستم محاسبه شده با استفاده از تابع ( )step در متلب آمده است.
منابع:
Fundamentals of Control Theory by Brian Douglas
C. H. Houpis, S. N. Sheldon, and J. J. D'Azzo, Linear Control System Analysis and Design, 5th ed. Boca Raton, FL: CRC Press, 2013
Y. Bavafa-Toosi, Introduction to Linear Control Systems. Amsterdam, Netherlands: Elsevier, 2017
K. Ogata, Modern Control Engineering, 5th ed. Upper Saddle River, NJ: Pearson, 2010
N. S. Nise, Control Systems Engineering, 6th ed. Hoboken, NJ: John Wiley & Sons, 2011
C.-T. Chen, Linear System Theory and Design, 3rd ed. New York, NY: Oxford University Press, 1999
G. F. Franklin, J. D. Powell, and A. Emami-Naeini, Feedback Control of Dynamic Systems, 7th ed. Boston, MA: Pearson, 2014
#کنترل_خطی #کنترل_مدرن #کنترل_مقاوم #کنترل_فازی #کنترل_کنترل_هوشمند #کنترل_دیجیتال #کنترل_پیش_بین_مبتنی_بر_مدل #کنترل_بهینه #کنترل_چند_متغییره #کنترل_کلاسیک #کنترل_اتوماتیک #کنترل_عصبی #کنترل_چند_عاملی #کنترل_شبکهای #کنترل_تطبیقی #کنترل #کنترل_غیر_خطی #مهندسی_کنترل #متلب #سیمولینک#متلب_سیمولینک #تابع_تبدیل #معادلات_حالت #مدل_سازی #شبیهسازی #کنترل_مبتنی_بر_داده #کنترل_سیستم #سیستم #بهینه_سازی #سنسور #فیدبک #بازخورد