مقدمهای بر رویتپذیری و رویتگرهای حلقه باز با متلب
در این مقاله آموزشی، مقدمهای کوتاه بر رویتگرهای حلقه باز ارائه میدهیم. در این مقاله، شما یاد خواهید گرفت
- 1) مفهوم مشاهدهپذیری
2) چگونه میتوان حالت اولیه یک سیستم دینامیکی خطی را با استفاده از یک مشاهدهگر حلقه باز تخمین زد
3) چگونه میتوان مفهوم مشاهدهپذیری عددی را به درستی درک کرد
انگیزه ایجاد این آموزش از این واقعیت ناشی میشود که دانشجویان اغلب در درک مفهوم مشاهدهپذیری مشکل دارند و اغلب نیاز به مشاهدهگر را درک نمیکنند. این امر از این واقعیت ناشی میشود که مفهوم مشاهدهپذیری اغلب ابتدا با فرض سیستمهای پیوسته در زمان آموزش داده میشود. ریاضیات مورد نیاز برای توصیف سیستمهای پیوسته در زمان پیچیدهتر از ریاضیات لازم برای توصیف سیستمهای گسسته در زمان است. این شامل انتگرالهایی است که برای عبارات برداری و ماتریسی اعمال میشوند که اغلب شامل نماییهای ماتریسی هستند. درک این مفاهیم ممکن است برای یک دانشجوی مهندسی متوسط دشوار باشد.
به جای معرفی مفهوم مشاهدهپذیری با فرض یک سیستم پیوسته در زمان، این مفهوم را با فرض یک سیستم گسسته در زمان ارائه خواهیم داد. به این ترتیب، ریاضیات لازم برای درک مفاهیم اساسی را به طور قابل توجهی ساده میکنیم.
بنابراین، بیایید فوراً با در نظر گرفتن مثالی که در شکل زیر نشان داده شده است، نیاز به تحلیل مشاهدهپذیری را توضیح دهیم.
شکل ۱: سیستم جرم-فنر دوگانه که برای نشان دادن مفهوم مشاهدهپذیری استفاده شده است
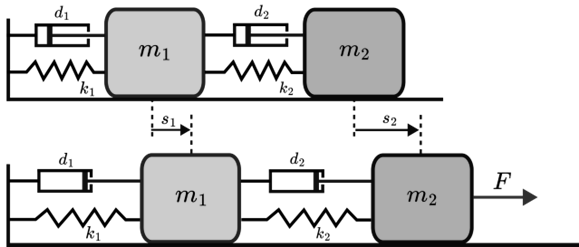
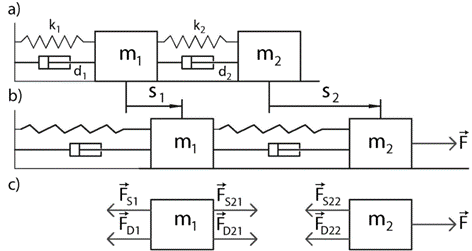
شکل بالا یک مدل اولیه از دو جرم متصل به فنرها و میراگرها را نشان میدهد. نیروی F جرم دوم را به حرکت در میآورد. معادلات حاکم بر رفتار این سیستم بسیار شبیه به معادلات حرکت تعدادی از سیستمهای مکانیکی و الکتریکی، مانند مدارهای الکتریکی و الکترونیکی، سیستمهای مکانیکی که حرکت آنها توسط معادلات نیوتن توصیف میشود، بازوهای رباتیک و غیره است.
مدل فضای حالت سیستم دوگانه جرم-فنر-میراگر
{
}
در قسمت بالا، ما یک مدل فضای حالت از این سیستم را استخراج کردیم. حالتها عبارتند از:
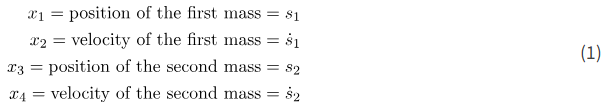
برای توسعه یک کنترل فیدبک، اغلب لازم است اطلاعاتی در مورد همه حالتها: x1، x2، x3 و x4 به دست آوریم. با این حال، در عمل، ما فقط میتوانیم یک متغیر حالت واحد، مانند مثلاً موقعیت x1 یا x3 را مشاهده کنیم. تحلیل مشاهدهپذیری سعی میکند به این نوع سؤالات پاسخ دهد.
آیا میتوان بردار حالت کامل (تمام متغیرهای حالت x1، x2، x3 و x4) را تنها با اندازهگیری موقعیت جرم اول در طول زمان بازسازی کرد؟ یعنی آیا میتوان سریهای زمانی x2، x3 و x4 را تنها با مشاهده سریهای زمانی x1 بازسازی کرد؟
اگر بازسازی تمام متغیرهای حالت دیگر تنها با اندازهگیری x1 امکانپذیر نباشد، پس برای بازسازی بردار حالت کامل، به مشاهده چند متغیر حالت نیاز داریم؟
سیستم خطی گسسته در زمان زیر را در نظر بگیرید

که در آن \mathbf{x}_{k}\in \mathbb{R}^{n} حالت سیستم در نمونه زمان گسسته k، \mathbf{y}_{k}\in \mathbb{R}^{r} خروجی سیستم در نمونه زمان گسسته k و A و C ماتریسهای سیستم هستند. خروجی سیستم \mathbf{y}_{k} معمولاً توسط یک حسگر مشاهده میشود. با این حال، حالت سیستم \mathbf{x}_{k} معمولاً به طور مستقیم قابل مشاهده نیست.
توجه داشته باشید که ما فرض کردهایم که ورودیها بر دینامیک سیستم ما تأثیری ندارند. این کار برای وضوح ارائه انجام شده است زیرا ورودیها بر مشاهدهپذیری سیستم تأثیری ندارند. همچنین میتوانیم به راحتی رویکرد خود را تغییر دهیم تا ورودیهای سیستم را نیز در نظر بگیریم.
بیایید مسئله زیر را در نظر بگیریم. وظیفه ما تخمین حالت اولیه سیستم ∈x∈0 (حالت سیستم ∈x∈k∈ در نمونه زمان گسسته k=0) از دنباله خروجیهای مشاهده شده ∈y∈0، ∈y∈1، ∈y∈2، ∈d، ∈y∈M-1 است که در آن M تعداد کل خروجیها (مشاهدات) است. این مسئله در واقع مسئله مشاهدهپذیری برای سیستم زمان گسسته (2) است.
بنابراین چگونه میتوان این مسئله را به صورت ریاضی فرموله و حل کرد؟
با انتشار معادله حالت سیستم (2) در زمان گسسته، داریم

با ترکیب این معادلات با معادله خروجی، به دست میآوریم

این معادلات را میتوان به فرم برداری-ماتریسی نوشت
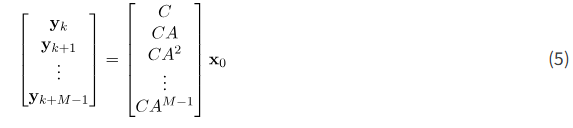
معادله آخر را میتوان به صورت فشرده نوشت

که
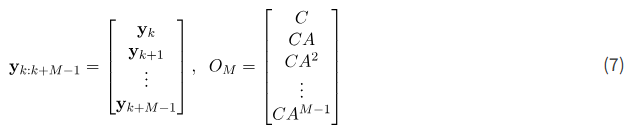
وقتی M=n باشد، که در آن n مرتبه حالت سیستم است، ماتریس O_{n} (ماتریس O_{M} برای M=n) ماتریس مشاهدهپذیری نامیده میشود.
نماد y_{k:k+M-1} نشان دهنده بردار بالابر است. بردارهای بالابر با "بالا بردن" بردارهای زیرین در طول زمان تشکیل میشوند. این بدان معناست که بردار y_{k:k+M-1} با روی هم قرار دادن بردارهای y_{k}، y_{k+1}، ldots و y_{k+M-1} تشکیل میشود. نمادگذاری k:k+M-1 به این معنی است که لحظه شروع برای بالابردن k و لحظه پایان k+M-1 است. با قرار دادن k=0 در (6)، به دست میآوریم

معادله آخر مهم است زیرا به ما نشان میدهد که مسئله مشاهدهپذیری، تعیین حالت اولیه \mathbf{x}_{0} از بردار مشاهده \mathbf{y}_{0:M-1} است. از آنجایی که معادله آخر نشاندهنده یک دستگاه معادلات خطی است، مسئله مشاهدهپذیری معادل مسئله حل دستگاه معادلات خطی است که در آن متغیرهای مجهول، ورودیهای بردار \mathbf{x}_{0} هستند. برای اطمینان از اینکه این دستگاه یک جواب منحصر به فرد دارد، یا به طور معادل برای اطمینان از مشاهدهپذیر بودن دستگاه، در کلیترین حالت، لازم و کافی است که:
- 1) تعداد نمونههای مشاهده M بزرگتر یا مساوی n است، که در آن n مرتبه حالت سیستم است.
2) \text{rank}\Big(O_{M}\Big)=n. این بدان معناست که ماتریس مشاهدهپذیری O_{M} رتبه کامل دارد.
در اینجا، باید چند نکته مهم را در نظر داشت. شرط (1) برای کلیترین حالت بیان شده است. با این حال، ممکن است اتفاق بیفتد که بعد خروجی r (بعد بردار \mathbf{y}_{k}) به گونهای باشد که بتوانیم اطمینان حاصل کنیم که ماتریس O_{M} حتی اگر M<n باشد، رتبه کامل دارد. به عنوان مثال، این سیستم را در نظر بگیرید

که در آن I\in \mathbb{R}^{n \times n} یک ماتریس همانی است. در مورد این سیستم، M=1، مشاهدهپذیری سیستم را تضمین میکند زیرا ماتریس C برابر با ماتریس همانی است و ماتریسهای همانی معکوسپذیر هستند. در عمل، لازم نیست تعداد نمونههای M بزرگتر از n باشد. دلیل این امر این است که ورودیهای CA^{M} برای M >n را میتوان به صورت ترکیبهای خطی CA^{P} بیان کرد، که در آن P=0,1,2,\ldots, n. این از قضیه کیلی-همیلتون نتیجه میشود. با این حال، در صورت وجود نویز اندازهگیری در معادله (2)، ممکن است گرفتن نمونههای بیشتر M مفید باشد (و M باید بزرگتر از n باشد)، زیرا به این ترتیب، میتوان حساسیت تخمین حالت اولیه را از خروجیهای مشاهده شده کاهش داد.
فرض میکنیم که شرایط (1) و (2) برقرار هستند. میتوانیم معادله (8) از سمت چپ را در O_{M}^{T} ضرب کنیم و در نتیجه، داریم:

سپس، از آنجایی که ماتریس O_{M} دارای رتبه ستونی کامل است، ماتریس O_{M}^{T}O_{M} معکوسپذیر است و از (10)، داریم:

معادله (11) راه حل مسئله مشاهدهپذیری است. ما یک تخمین حالت اولیه را به عنوان تابعی از مشاهدات بدست آوردهایم: ...
اکنون که مفهوم مشاهدهپذیری را به صورت غیررسمی معرفی کردیم، میتوانیم یک تعریف رسمی از آن ارائه دهیم:
تعریف مشاهدهپذیری: سیستم (2) مشاهدهپذیر است، اگر هر حالت اولیه \mathbf{x}_{k} به طور منحصر به فرد توسط خروجیهای مشاهده شده \mathbf{y}_{k}، \mathbf{y}_{k+1}، \mathbf{y}_{k+2}، \ldots، \mathbf{y}_{k+M}، برای یک عدد صحیح مثبت متناهی M تعیین شود.
همچنین میتوانیم شرط رتبه مشاهدهپذیری را به صورت زیر بیان کنیم:
شرط رتبه مشاهدهپذیری: سیستم (2) مشاهدهپذیر است اگر و تنها اگر \text{rank}\Big(O_{n}\Big)=n باشد.
از آنچه گفته شد، نتیجه میشود که میتوانیم با بررسی رتبه ماتریس On، شرط مشاهدهپذیری را بررسی کنیم.
با این حال، این معیار مشکل زیر را دارد. به عبارت دیگر، به طور رسمی، ماتریس ممکن است رتبه کامل داشته باشد، اما ممکن است نزدیک به ماتریس تکین باشد. یعنی، عدد شرط آن ممکن است بسیار بزرگ باشد یا کوچکترین مقدار تکین آن ممکن است نزدیک به صفر باشد. این نشان میدهد که برای بررسی مشاهدهپذیری سیستم، معمولاً محاسبه عدد شرط یا کوچکترین مقدار تکین مناسبتر است.
بیایید با استفاده از مثال ابتدای این پست، تمام این مفاهیم را به صورت عددی نشان دهیم. در پست قبلی خود، ضمن توضیح روش شناسایی زیرفضا، این مثال را معرفی کردیم. این مثال به طور خلاصه در زیر آمده است. برای کامل بودن، شکل مربوط به این مثال را تکرار میکنیم.
شکل ۲: سیستم جرم-فنر دوگانه
مدل فضای حالت در زیر آورده شده است
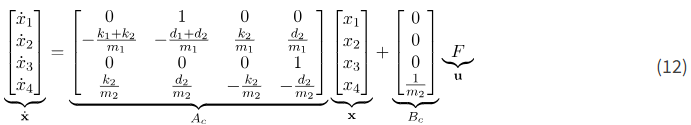
ما فرض میکنیم که فقط موقعیت اولین جسم را میتوان مستقیماً مشاهده کرد. این امر را میتوان با استفاده از مثلاً حسگرهای فاصله مادون قرمز به دست آورد. تحت این فرض، معادله خروجی به شکل زیر است:

مرحله بعدی تبدیل مدل فضای حالت (12)-(13) در حوزه زمان گسسته است. به دلیل سادگی و خواص پایداری خوب، از روش اویلر معکوس برای انجام گسستهسازی استفاده میکنیم. این روش مشتق حالت را به صورت زیر تقریب میزند:

که در آن h گام زمانی گسستهسازی است. برای سادگی، فرض کردیم که شاخص زمان گسسته ورودی k-1 است. همچنین میتوانیم فرض کنیم که شاخص زمان گسسته ورودی k است. با این حال، هنگام شبیهسازی دینامیک سیستم، از k=1 شروع خواهیم کرد. از معادله آخر، داریم

که در آن A=(I-hA_{c})^{-1} و B=hAB_{c}. از سوی دیگر، معادله خروجی بدون تغییر باقی میماند.

ما ورودی را نادیده میگیریم و بدون از دست دادن کلیت، شاخص زمان را از k به k+1 تغییر میدهیم و در نتیجه، مدل فضای حالت نهایی را به دست میآوریم.

در مرحله بعد، کد MATLAB را معرفی میکنیم. ابتدا پارامترهای مدل و سایر متغیرها را تعریف میکنیم.
کد متلب:
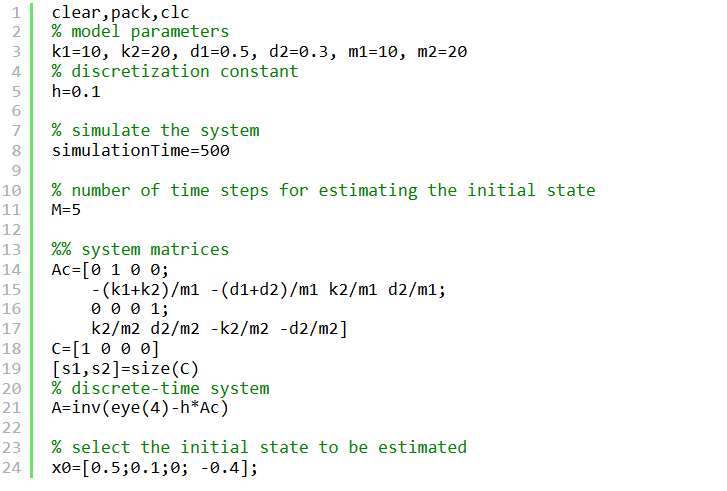
ابتدا، پارامترهای مدل مانند میرایی، سختی و جرم را تعریف میکنیم. ما از ثابت گسستهسازی h=0.1 و زمان کل شبیهسازی ۵۰۰ استفاده میکنیم. سپس، ماتریسهای سیستم A و C را تعریف میکنیم و ماتریس گسستهسازی شده A را تعریف میکنیم. حالت اولیه را تعریف میکنیم. این حالت برای شبیهسازی پاسخ سیستم استفاده میشود و ما این حالت اولیه را تخمین خواهیم زد. ما نمونههای زمانی M=5 را برای تشکیل بردارهای بالابر و ماتریس مشاهدهپذیری انتخاب میکنیم.
در مرحله بعد، پاسخ سیستم را شبیهسازی میکنیم. خطوط کد زیر پاسخ سیستم را شبیهسازی کرده و ماتریس مشاهدهپذیری را تشکیل میدهند.
کد متلب:

پاسخ سیستم در شکل زیر نشان داده شده است.
شکل ۳: خروجی شبیهسازیشده سیستم با شروع از حالت اولیه.
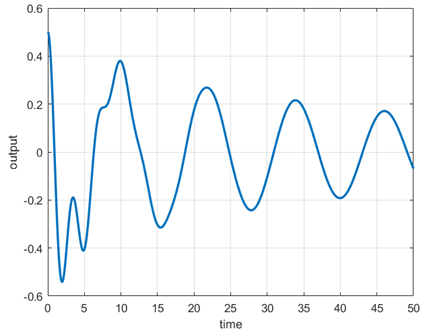
در مرحله بعد، حالت اولیه را با استفاده از معادله (11) تخمین میزنیم. سپس با محاسبه خطای تخمین نسبی، تخمین را با حالت اولیه مقایسه میکنیم. سپس، مقادیر تکین ماتریس مشاهدهپذیری را محاسبه کرده و عدد شرط را محاسبه میکنیم.
کد متلب:

شما میتوانید این کد را با تغییر ساختار ماتریس C اصلاح کنید. به عنوان مثال، میتوانید تأثیر مشاهدهی یک متغیر دیگر را بررسی کنید (مثلاً، چه اتفاقی میافتد وقتی C=\begin{bmatrix} 0 & 1 & 0 & 0 \end{bmatrix}). این موضوع در ویدیوی یوتیوب همراه توضیح داده شده است. همچنین، میتوانید تعداد مراحل مشاهدهپذیری را تغییر داده و پارامترهای سیستم را اصلاح کنید.