مقدمهای بر سینماتیک معکوس رباتها
در این مقاله آموزشی، نحوه حل مسئله سینماتیک معکوس یک ربات با دو درجه آزادی را توضیح میدهیم. در این حالت نسبتاً ساده، میتوان مسئله سینماتیک معکوس را به صورت تحلیلی حل کرد (یعنی، حل فرم بسته را محاسبه کرد). هدف از این مثال، معرفی مسئله سینماتیک معکوس است.
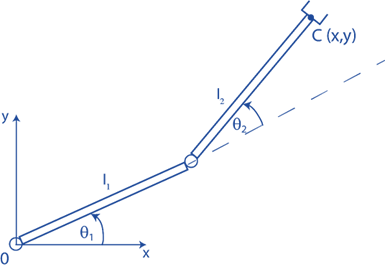
یک بازوی مکانیکی با دو درجه آزادی چرخشی θ1 و θ2 که در شکل زیر نشان داده شده است را در نظر بگیرید.
شکل ۱: بازوی رباتیک دو درجه آزادی برای توضیح مسئله سینماتیک معکوس
مسئله سینماتیک معکوس را میتوان به صورت زیر فرموله کرد:
با توجه به مختصات x و y نقطه C (مختصات جهانی)، زوایای θ1 و θ2 (مختصات مفصل محلی) را محاسبه کنید.
در بیان مسئله سینماتیک معکوس، فرض بر این است که طول بخشهای رباتیک l1 و l2 داده شده است.
از شکل ۱، داریم

با به توان دو رساندن دو معادله آخر و جمع کردن آنها با هم، به دست میآوریم
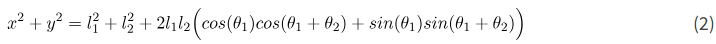
در مرحله بعد، از فرمول مثلثاتی زیر استفاده میکنیم
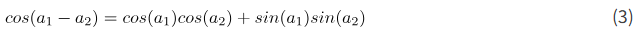
با استفاده از این فرمول با a_{1}=\theta_{1} و a_{2}=\theta_{2}، از (2)، داریم:

که در آن از اتحاد cos(-\theta_{2})=cos(\theta_{2}) استفاده کردهایم (تابع کسینوس یک تابع زوج است). از معادله آخر، داریم:

معادله آخر ما را قادر میسازد تا زاویه θ1 را به عنوان تابعی از x و y محاسبه کنیم.
در اینجا، باید یک نکته مهم را در نظر گرفت. فرض کنید که سمت راست معادله (5) برابر با 0.5 است. برای محاسبه θ2، باید این معادله را حل کنیم.

این معادله تعداد نامتناهی جواب دارد، با این حال، تنها دو جواب وجود دارد که از نظر فیزیکی منحصر به فرد و از نظر فیزیکی واقعبینانه هستند، این جوابها عبارتند از

شکل زیر سناریوی مشابهی را نشان میدهد. میتوانیم مشاهده کنیم که دو احتمال برای رسیدن به نقطه C وجود دارد (موقعیتهای دستکاری قرمز و سیاه).
شکل ۲: غیرمنحصر به فرد بودن مسئله سینماتیک معکوس
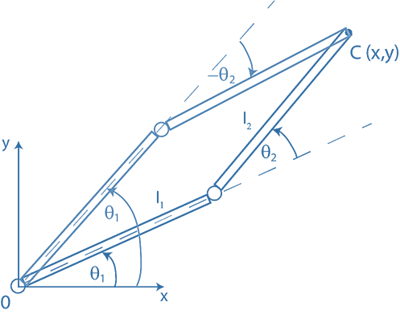
این یک وضعیت رایج هنگام حل مسئله سینماتیک معکوس است.
زاویه \theta_{1} را با تحلیل شکل زیر تعیین خواهیم کرد.
شکل ۳: شکل برای تعیین \theta_{1}
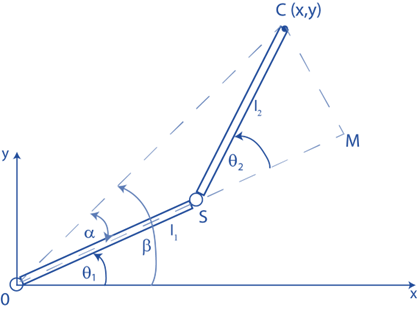
از شکل 3، داریم

که در آن \beta و \alpha زوایایی هستند که در شکل زیر نشان داده شدهاند. ما \theta_{1} را با استفاده از تابع tan() پیدا خواهیم کرد. از (8)، داریم

در مرحله بعد، از فرمول زیر استفاده خواهیم کرد
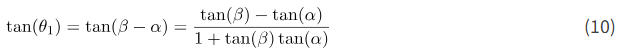
از شکل 3، داریم

از طرف دیگر، از مثلثهای OMC و CMS، داریم
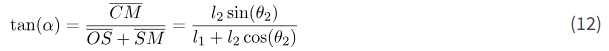
در اینجا باید توجه داشت که α فقط تابعی از β2 است، بنابراین وقتی β2 از (5) تعیین شود، میتوانیم α را از (12) پیدا کنیم.
با جایگزینی (11) و (12) در (10)، نتیجه نهایی را برای θ_{1} بدست میآوریم.
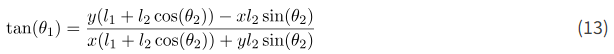
حل مسئله سینماتیک معکوس در متلب
در این بخش، یاد میگیریم که چگونه یک مسئله سینماتیک معکوس را در متلب حل کنیم. در پست قبلی ما، که میتوانید آن را اینجا پیدا کنید، مقدمهای بر مسئله سینماتیک معکوس ارائه دادیم. ما توضیح دادیم که چگونه مسئله سینماتیک معکوس را به صورت تحلیلی حل کنیم. با این حال، در بسیاری از موارد یا یافتن راهحل تحلیلی امکانپذیر نیست یا راهحل تحلیلی بسیار پیچیده است. در چنین مواردی، ترجیح داده میشود که راهحل را به صورت عددی تقریب بزنیم.
یک بازوی مکانیکی با دو درجه آزادی چرخشی θ1 و θ2 که در شکل 1 نشان داده شده است را در نظر بگیرید.
از شکل ۱، داریم
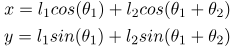
حال، برای x و y داده شده، و برای l1 و l2 داده شده، معادلات بالا یک سیستم معادلات غیرخطی را نشان میدهند که در آن متغیرهای مجهول θ1 و θ2 هستند.
ابتدا، معادلات بالا را به صورت زیر تبدیل میکنیم
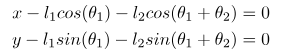
ابتدا، یک تابع ملتب تعریف میکنیم که سیستم بالا را توصیف میکند.

ما این تابع را در فایلی به نام «kinematics.m» ذخیره میکنیم و پوشهای که این تابع در آن ذخیره شده است را به مسیر متلب اضافه میکنیم.
این تابع متلب از کد متلب زیر فراخوانی میشود.

برای حل دستگاه معادلات غیرخطی، باید x، y، l1 و l2 را مشخص کنیم. این کار در خطوط کد ۶-۷ انجام میشود. دو حالت آزمایشی را در نظر میگیریم. در حالت اول، θ1=0 و θ2=0. حالت دوم θ1=0 و θ2=0 است. سپس برای این حالتها، حدسهای اولیه θ1 و θ2 را تعریف میکنیم. برای حل دستگاه معادلات غیرخطی، باید شرایط اولیه را مشخص کنیم. در خط کد ۱۴، حدسهای اولیه را به رادیان تبدیل میکنیم. خط کد ۱۷ برای حل دستگاه معادلات غیرخطی استفاده میشود. خط کد ۱۹ برای تأیید جواب، با ارزیابی سمت راست (معادله دوم) استفاده میشود. خط کد ۲۱ برای تبدیل جواب به درجه استفاده میشود.
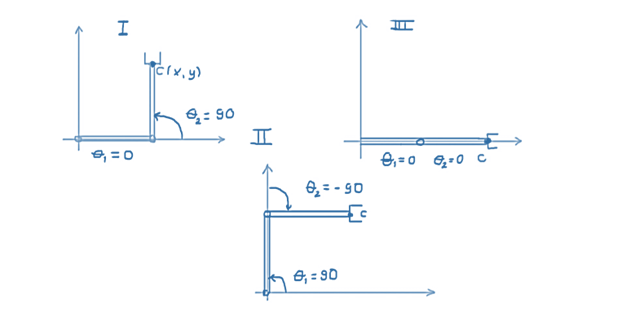
موارد آزمایشی مورد استفاده در این آموزش، در شکل زیر توضیح داده شده است.
منابع:
Fundamentals of Control Theory by Brian Douglas
C. H. Houpis, S. N. Sheldon, and J. J. D'Azzo, Linear Control System Analysis and Design, 5th ed. Boca Raton, FL: CRC Press, 2013
Y. Bavafa-Toosi, Introduction to Linear Control Systems. Amsterdam, Netherlands: Elsevier, 2017
K. Ogata, Modern Control Engineering, 5th ed. Upper Saddle River, NJ: Pearson, 2010
N. S. Nise, Control Systems Engineering, 6th ed. Hoboken, NJ: John Wiley & Sons, 2011
C.-T. Chen, Linear System Theory and Design, 3rd ed. New York, NY: Oxford University Press, 1999
G. F. Franklin, J. D. Powell, and A. Emami-Naeini, Feedback Control of Dynamic Systems, 7th ed. Boston, MA: Pearson, 2014
#کنترل_خطی #کنترل_مدرن #کنترل_مقاوم #کنترل_فازی #کنترل_کنترل_هوشمند #کنترل_دیجیتال #کنترل_پیش_بین_مبتنی_بر_مدل #کنترل_بهینه #کنترل_چند_متغییره #کنترل_کلاسیک #کنترل_اتوماتیک #کنترل_عصبی #کنترل_چند_عاملی #کنترل_شبکهای #کنترل_تطبیقی #کنترل #کنترل_غیر_خطی #مهندسی_کنترل #متلب #سیمولینک#متلب_سیمولینک #تابع_تبدیل #معادلات_حالت #مدل_سازی #شبیهسازی #کنترل_مبتنی_بر_داده #کنترل_سیستم #سیستم #بهینه_سازی #سنسور #فیدبک #بازخورد