توابع مهم و کاربردی نرم افزار متلب برای مهندسی کنترل
چکیده مطالب:
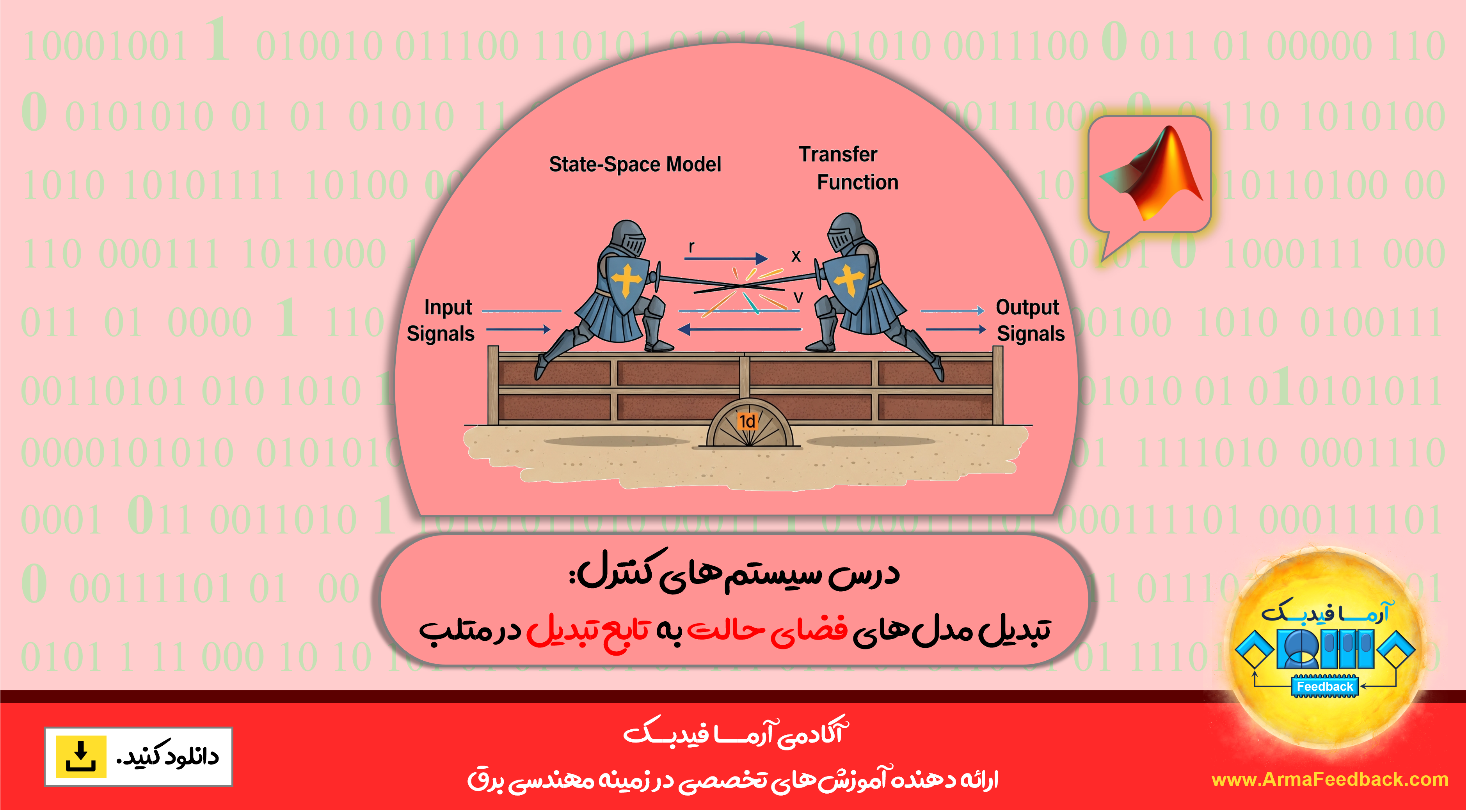
این متن به معرفی یک بسته نرمافزاری میپردازد که قابلیتهای متلب را برای مهندسی کنترل شبیهسازی میکند. این بسته توابع متنوعی را برای ساخت و تحلیل مدلهای خطی سیستمها (مانند تابع تبدیل و فضای حالت) ارائه میدهد. همچنین ابزارهایی برای اتصال سیستمها، تحلیل دینامیک و پاسخ زمانی/فرکانسی آنها، و طراحی جبرانسازها در اختیار مهندسان کنترل قرار میدهد. به طور خلاصه، این بسته به مدلسازی، شبیهسازی، تحلیل و طراحی سیستمهای کنترل کمک میکند.
این بسته شامل تعدادی تابع است که برخی از قابلیتهای متلب را برای مهندسی کنترل شبیهسازی میکنند.
ایجاد مدلهای خطی (Creating Linear Models):
| ایجاد یک سیستم تابع تبدیل | tf(num, den[, dt]) |
| ایجاد یک سیستم فضای حالت | ss(A, B, C, D[, dt]) |
| ساخت یک مدل داده پاسخ فرکانسی (FRD) | frd(frdata, omega[, dt]) |
| ایجاد یک تابع انتقال از صفرها، قطبها، بهره | zpk(zeros, poles, gain[, dt]) |
توابع کاربردی و تبدیلها (Utility Functions and Conversions):
| تبدیل اندازه به دسیبل (dB) | mag2db(mag) |
| تبدیل بهره بر حسب دسیبل (dB) به بزرگی | db2mag(db) |
| تبدیل یک سیستم زمان پیوسته به زمان گسسته با نمونهبرداری | c2d(sysc, Ts[, method, alpha, ...]) |
| تبدیل یک سیستم فضای حالت به یک تابع تبدیل | ss2tf(sys) |
| تبدیل یک تابع تبدیل به یک سیستم فضای حالت | tf2ss(sys) |
| بازگرداندن اشیاء داده تابع تبدیل برای یک سیستم | tfdata(sys) |
اتصالات سیستم (System Interconnections):
| اتصال سری سیستمهای ورودی/خروجی | series(sys1, sys2[, ..., sysn]) |
| اتصال موازی سیستمهای ورودی/خروجی | parallel(sys1, sys2[, ..., sysn]) |
| اتصال بازخوردی بین دو سیستم ورودی/خروجی | feedback(sys1[, sys2, sign]) |
| بازگرداندن عدد منفی یک سیستم | negate(sys, **kwargs) |
| اتصال مبتنی بر شاخص یک سیستمLTI | connect(sys, Q, inputv, outputv) |
| گروهبندی مدلهای LTI با اضافه کردن ورودیها و خروجیهای آنها | append(sys1, sys2[, ..., sysn]) |
بهره و دینامیک سیستم (System Gain and Dynamics):
| محاسبه بهره سیستم در حالت پایدار. | dcgain(...) |
| محاسبه قطبهای سیستم. | pole(sys) |
| محاسبه صفرهای سیستم. | zero(sys) |
| محاسبه فرکانسهای طبیعی سیستم، نسبتهای میرایی و قطبها. | damp(sys[, doprint]) |
| رسم نمودار قطب/صفر برای یک سیستم خطی. | pzmap(sys[, grid, plot]) |
تحلیل حوزه زمان (Time-Domain Analysis):
| پاسخ پله یک سیستم خطی. | step(sys[, T, input, output, return_x]) |
| پاسخ ضربه یک سیستم خطی. | impulse(sys[, T, input, output, return_x]) |
| پاسخ شرایط اولیه یک سیستم خطی. | initial(sys[, T, X0, input, output, return_x]) |
| شبیهسازی خروجی یک سیستم خطی. | lsim(sys[, U, T, X0]) |
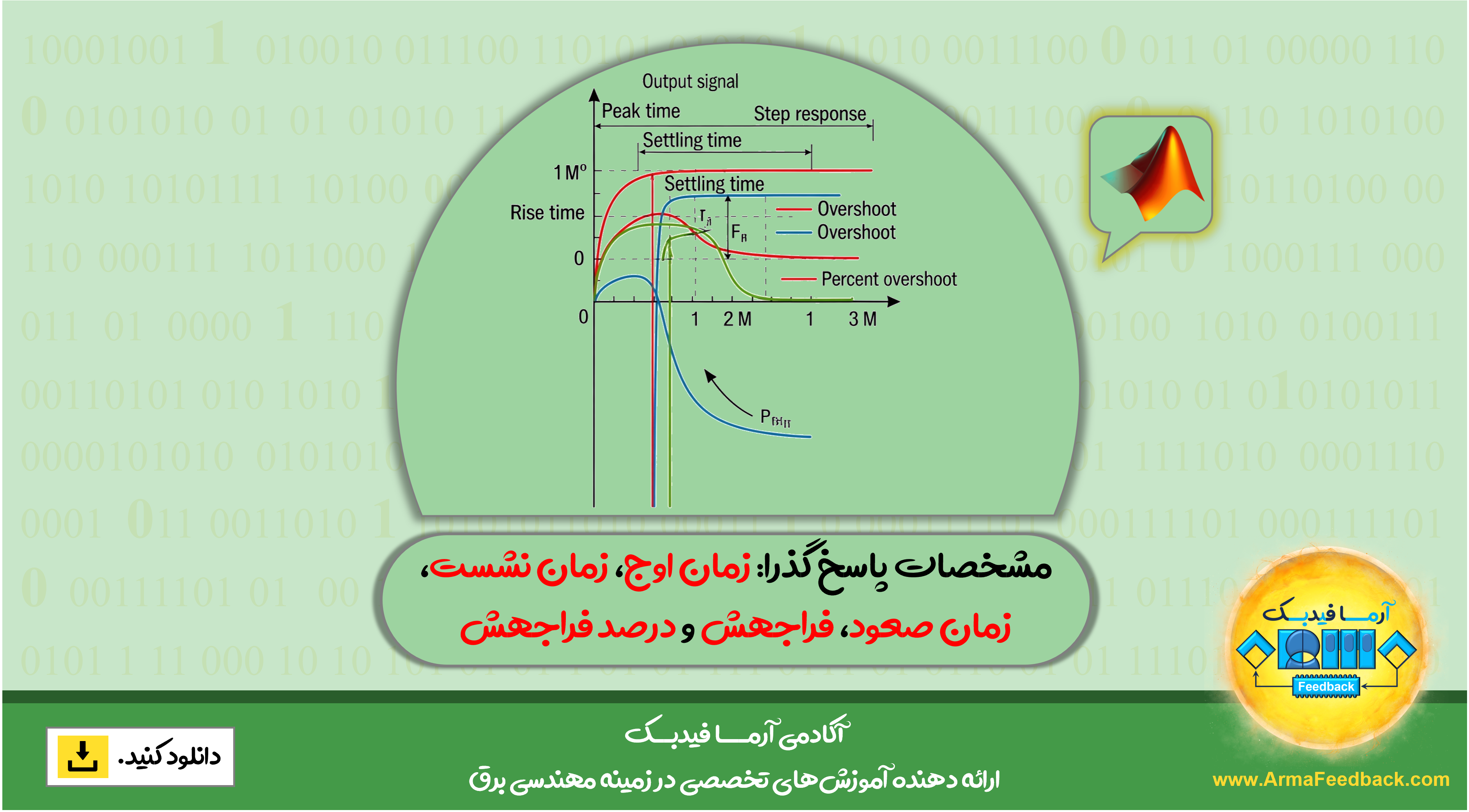
| مشخصات پاسخ پله (زمان صعود، زمان نشست و غیره). | stepinfo(sysdata[, T, yfinal, ...]) |
تحلیل حوزه فرکانس (Frequency-Domain Analysis):
| نمودار بودِ پاسخ فرکانسی. | bode(sys[, omega, dB, Hz, deg, ...]) |
| نمودار نایکوئیست پاسخ فرکانسی. | nyquist(syslist[, omega]) |
| حاشیههای بهره و فاز و فرکانسهای متقاطع مرتبط. | margin(sys) margin(mag, phase, omega) |
| نمودار نیکولز برای یک سیستم. | nichols(data[, omega, grid, title, ax, label]) |
| نمودار شبکهای نمودار نیکولز. | ngrid() |
| پاسخ فرکانسی یک سیستم LTI. | freqresp(sysdata[, omega, omega_limits, ...]) |
| ارزیابی تابع انتقال سیستم LTI در فرکانس مختلط. | evalfr(sys, x[, squeeze]) |
طراحی جبرانساز (Compensator Design):
| نمودار مکان هندسی ریشهها. | rlocus(sys[, gains, xlim, ylim, ...]) |
| مجموعهای از نمودارهای الهام گرفته از ابزار Sisotool در MATLAB. | sisotool(sys[, initial_gain, xlim_rlocus, ...]) |
| مقادیر ویژه حلقه بسته را قرار دهید. | place(A, B, p) |
| طراحی رگولاتور خطی درجه دوم. | lqr(A, B, Q, R[, N]) |
| طراحی رگولاتور خطی درجه دوم گسسته. | dlqr(A, B, Q, R[, N]) |
| تخمینگر خطی درجه دوم پیوسته (فیلتر کالمن). | lqe(A, G, C, QN, RN, [, NN]) |
| تخمینگر خطی درجه دوم گسسته (فیلتر کالمن). | dlqe(A, G, C, QN, RN, [, N]) |
مدلهای فضای حالت (State-space (SS) Models):
| ایجاد یک شیء فضای حالت تصادفی پایدار. | rss([states, outputs, inputs, strictly_proper]) |
| ایجاد یک سیستم فضای حالت تصادفی پایدار، زمان گسسته. | drss([states, outputs, inputs, strictly_proper]) |
| ماتریس کنترلپذیری. | ctrb(A, B[, t]) |
| ماتریس مشاهدهپذیری. | obsv(A, C[, t]) |
| گرامین (کنترلپذیری یا مشاهدهپذیری). | gram(sys, type) |
سادهسازی مدل (Model Simplification):
| حذف حالتهای غیرقابل کنترل یا غیرقابل مشاهده | minreal(sys[, tol, verbose]) |
| محاسبه مقادیر تکین هنکل | hsvd(sys) |
| مدل مرتبه کاهش یافته متوازن سیستم با مرتبه معین | balred(sys, orders[, method, alpha]) |
| کاهش مدل با حذف ورودی، خروجی یا حالت | modred(sys[, elim_states, method, ...]) |
| محاسبه مدل ERA بر اساس دادههای پاسخ ضربه | era(YY, r) |
| محاسبه پارامترهای مارکوف [D CB CAB ...] از دادهها | markov(Y, U, [, m]) |
تأخیرهای زمانی (Time Delays):
| یک سیستم خطی ایجاد کنید که تأخیر را تقریب بزن | pade(T[, n, numdeg]) |
حلکنندههای معادلات ماتریسی و جبر خطی (Matrix Equation Solvers and Linear Algebra):
| حل معادله لیاپانوف در زمان پیوسته | lyap(A, Q[, C, E, method]) |
| حل معادله لیاپانوف در زمان گسسته | dlyap(A, Q[, C, E, method]) |
| حل معادله ریکاتی جبری در زمان پیوسته | care(A, B, Q[, R, S, E, stabilizing, ...]) |
| حل معادله ریکاتی جبری در زمان گسسته | dare(A, B, Q, R[, S, E, stabilizing, ...]) |
توابع اضافی (Additional Functions):
| رسم پاسخ توابع تبدیل "دسته ۴ تایی" | gangof4(response) gangof4_plot(P, C, omega) |
| باز کردن یک زاویه فاز برای بدست آوردن یک منحنی پیوسته | unwrap(angle[, period]) |
توابع وارد شده از بستههای دیگر (Functions Imported from Other Packages):
| اعداد با فاصله مساوی را در یک بازه مشخص برمیگرداند. | linspace(start, stop[, num, endpoint, ...]) |
| اعداد با فاصله مساوی را در مقیاس لگاریتمی برمیگرداند. | logspace(start, stop[, num, endpoint, base, ...]) |
| نمایش فضای حالت به نمایش بهره قطب صفر. | ss2zpk(A, B, C, D[, input]) |
| نمایش صفر، قطب، بهره (z، p، k) را از نمایش صورت و مخرج یک فیلتر خطی برمیگرداند. | tf2zpk(b, a) |
| نمایش بهره قطب صفر به نمایش فضای حالت | zpk2ss(z, p, k) |
| نمایش تابع انتقال چندجملهای را از صفرها و قطبها برمیگرداند. | zpk2tf(z, p, k) |
منابع:
.The MathWorks Inc, www.mathworks.com: “MATLAB Version: 2024
#کنترل_خطی #کنترل_مدرن #کنترل_مقاوم #کنترل_فازی #کنترل_کنترل_هوشمند #کنترل_دیجیتال #کنترل_پیش_بین_مبتنی_بر_مدل #کنترل_بهینه #کنترل_چند_متغییره #کنترل_کلاسیک #کنترل_اتوماتیک #کنترل_عصبی #کنترل_چند_عاملی #کنترل_شبکهای #کنترل_تطبیقی #کنترل #کنترل_غیر_خطی #مهندسی_کنترل #متلب #سیمولینک#متلب_سیمولینک #تابع_تبدیل #معادلات_حالت #مدل_سازی #شبیهسازی #کنترل_مبتنی_بر_داده #کنترل_سیستم #سیستم #بهینه_سازی #سنسور #فیدبک #بازخورد