درس های سیستمهای کنترل: تبدیل لاپلاس
در این مقاله آموزشی، یک ابزار عددی مهم برای تحلیل و طراحی سیستمهای کنترل را معرفی میکنیم. نام این ابزار عددی، تبدیل لاپلاس است.
کاربردهای زیادی برای تبدیل لاپلاس در سیستمهای کنترل وجود دارد. به عنوان مثال، این تبدیل برای تحلیل پایداری سیستمهای کنترل استفاده میشود. همچنین، این تبدیل برای محاسبه پاسخ سیستم به شرایط اولیه و سیگنالهای ورودی از پیش تعیین شده استفاده میشود. به یاد داشته باشید که در درس ریاضیات معادلات دیفرانسیل معمولی، از تبدیل لاپلاس برای تبدیل معادلات دیفرانسیل خطی به معادلات جبری استفاده کردهاید. با دستکاری این معادلات جبری، توانستید معادلات دیفرانسیل خطی اولیه را حل کنید.
بنابراین، تبدیل لاپلاس را معرفی میکنیم. فرض کنید s=\sigma+j \omega یک متغیر مختلط باشد، که در آن \sigma و \omega بخشهای حقیقی و موهومی هستند. فرض کنید f(t) تابعی از زمان t باشد. سپس تبدیل لاپلاس تابع f(t) به صورت زیر تعریف میشود:

چند نکته لازم است. نماد 0^{-} به این معنی است که انتگرالگیری از 0-\epsilon شروع شده است که در آن اپسیلون یک کمیت بینهایت کوچک است. ما اغلب 0^{-} را به صورت ساده صفر مینویسیم. همانطور که از نامش پیداست، تبدیل لاپلاس تابع حوزه زمان را به معادل حوزه مختلط آن تبدیل میکند. انتگرالگیری از 0 تا \infty انجام میشود و ممکن است از خود بپرسیم، این انتگرال چه زمانی وجود دارد؟ ما وارد جزئیات ریاضی نمیشویم، با این حال، برای تعداد زیادی از توابع f(t)، تابع e^{-st} از انفجار حاصلضرب f(t) e^{-st} جلوگیری میکند.
اکنون تبدیل لاپلاس چند تابع مشخصه مورد استفاده در سیستمهای کنترل را محاسبه میکنیم.
تبدیل لاپلاس یک تابع پلهای (تابع ثابت)
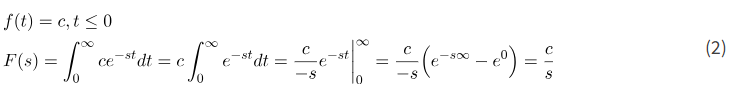
تبدیل لاپلاس یک تابع شیبدار (تابع ثابت)

برای حل این مشکل، باید از قانون انتگرالگیری جزء به جزء استفاده کنیم. یک روش ساده برای استخراج قانون انتگرالگیری جزء به جزء وجود دارد. فرض کنید u و v دو تابع باشند، سپس با مشتقگیری از این دو تابع، داریم:

از آخرین معادله، به دست میآوریم

بنابراین، اکنون انتگرالگیری جزء به جزء را در معادله (3) اعمال میکنیم. با انجام جایگزینیهای زیر

ما به دست میآوریم
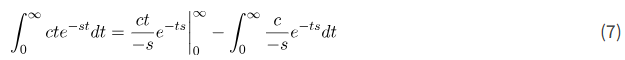
بیایید اولین جمله را ارزیابی کنیم
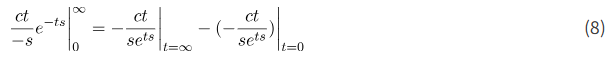
جمله اول برابر با صفر است زیرا تابع e^{ts} سریعتر از تابع t رشد میکند. به عنوان یک روش جایگزین، میتوانید این نتیجه را با استفاده از قانون هوپیتال به دست آورید. جمله دوم برابر با صفر است.
با محاسبهی عبارت دوم در معادلهی (7)، به دست میآوریم

تبدیل لاپلاس یک تابع نمایی

ما داریم:
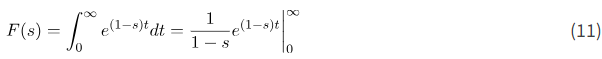
تحت شرایطی که انتگرال وجود داشته باشد (شرط بعداً توضیح داده خواهد شد). برای ارزیابی آخرین عبارت، باید متغیر مختلط s را به صورت زیر بنویسیم: s=\sigma + j\omega. سپس میتوانیم بنویسیم:

در مرحله بعد، باید از فرمول اویلر استفاده کنیم. این فرمول به شکل زیر است:

با اعمال این فرمول به معادله (12)، به دست میآوریم
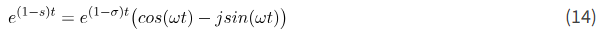
تحت این شرط که 1< \sigma باشد، توان در عبارت آخر منفی است. تحت این شرط، داریم

از آنجا که e^{(1-\sigma)\infty} =0 و e^{(1-\sigma)0} =1. با جایگذاری این عبارت در معادله (11)، داریم:

تبدیل لاپلاس یک تابع هارمونیک (تابع سینوسی)

که در آن w ثابت است. برای حل این مسئله، باید فرمول اویلر را به خاطر بیاوریم. این فرمول به شکل زیر است:

با استفاده از این فرمول، میتوانیم بنویسیم

با جایگذاری معادله (19) در معادله (17)، به دست میآوریم
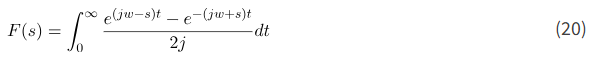
منابع:
Fundamentals of Control Theory by Brian Douglas
C. H. Houpis, S. N. Sheldon, and J. J. D'Azzo, Linear Control System Analysis and Design, 5th ed. Boca Raton, FL: CRC Press, 2013
Y. Bavafa-Toosi, Introduction to Linear Control Systems. Amsterdam, Netherlands: Elsevier, 2017
K. Ogata, Modern Control Engineering, 5th ed. Upper Saddle River, NJ: Pearson, 2010
N. S. Nise, Control Systems Engineering, 6th ed. Hoboken, NJ: John Wiley & Sons, 2011
C.-T. Chen, Linear System Theory and Design, 3rd ed. New York, NY: Oxford University Press, 1999
G. F. Franklin, J. D. Powell, and A. Emami-Naeini, Feedback Control of Dynamic Systems, 7th ed. Boston, MA: Pearson, 2014
#کنترل_خطی #کنترل_مدرن #کنترل_مقاوم #کنترل_فازی #کنترل_کنترل_هوشمند #کنترل_دیجیتال #کنترل_پیش_بین_مبتنی_بر_مدل #کنترل_بهینه #کنترل_چند_متغییره #کنترل_کلاسیک #کنترل_اتوماتیک #کنترل_عصبی #کنترل_چند_عاملی #کنترل_شبکهای #کنترل_تطبیقی #کنترل #کنترل_غیر_خطی #مهندسی_کنترل #متلب #سیمولینک#متلب_سیمولینک #تابع_تبدیل #معادلات_حالت #مدل_سازی #شبیهسازی #کنترل_مبتنی_بر_داده #کنترل_سیستم #سیستم #بهینه_سازی #سنسور #فیدبک #بازخورد