طراحی کنترل کننده برای سیستم موقعیت توپ بر روی میله در متلب
چکیده مطالب:
این مقاله درباره طراحی کنترلکننده برای سیستم موقعیت توپ بر روی میله با استفاده از متلب است. ابتدا، سیستم مدلسازی میشود؛ روابط حاکم و پارامترها معرفی شده، معادلات خطیسازی شده و به دو صورت تابع تبدیل و فضای حالت نمایش داده میشوند. در ادامه، تحلیل پایداری سیستم حلقه باز انجام میگیرد و نشان داده میشود که سیستم ناپایدار است. سپس، یک کنترلکننده فیدبک حالت کامل طراحی میشود تا سیستم پایدار شده و به معیارهای عملکردی مورد نظر (زمان نشست و فراجهش) دست یابد. در نهایت، برای حذف خطای حالت پایدار، یک جبرانکننده ورودی مرجع به سیستم اضافه میگردد و نتایج شبیهسازی، دستیابی به اهداف طراحی را تأیید میکنند.
فهرست مطالب:
- 1) روابط حاکم
2) پارامترهای سیستم
3) معیارهای طراحی
4) معادلات سیستم
5) مدل سیستم
6) نقشه قطب/صفر
7) پاسخ پله حلقه باز
8) کنترلکننده فیدبک حالت کامل
9) ورودی مرجع
10) منابع
روابط حاکم:
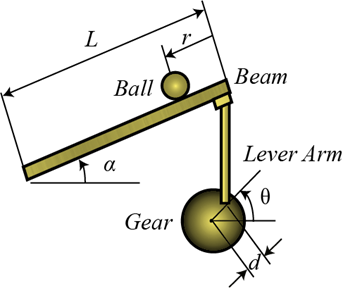
یک توپ روی یک تیر قرار داده شده است، شکل زیر را ببینید، که در آن اجازه دارد با ۱ درجه آزادی در امتداد طول تیر بغلتد. یک بازوی اهرمی در یک انتها و یک چرخدنده سروو در انتهای دیگر به تیر متصل است. با چرخش چرخدنده سروو به اندازه زاویه θ، اهرم زاویه تیر را به اندازه α تغییر میدهد. هنگامی که زاویه از حالت افقی تغییر میکند، گرانش باعث میشود توپ در امتداد تیر بغلتد. یک کنترلکننده برای این سیستم طراحی خواهد شد تا موقعیت توپ قابل دستکاری باشد.
پارامترهای سیستم:
برای این مسئله، فرض میکنیم که توپ بدون لغزش میغلتد و اصطکاک بین تیر و توپ ناچیز است. ثابتها و متغیرها برای این مثال به شرح زیر تعریف میشوند:
(m): جرم توپ 0.11 کیلوگرم
(R): شعاع توپ 0.015 متر
(d): جابجایی بازوی اهرم 0.03 متر
(g): شتاب گرانش 9.8 متر بر ثانیه
(L): طول تیر 1.0 متر
(J): گشتاور اینرسی توپ 9.99e-6 کیلوگرم بر متر مربع
(r): مختصات موقعیت توپ
(alpha): مختصات زاویه پرتو
(theta): زاویه چرخ دنده سروو
معیارهای طراحی کنترل کننده:
زمان نشست کمتر از ۳ ثانیه
فراجهش کمتر از ۵٪
معادلات سیستم:
مشتق دوم زاویه ورودی آلفا در واقع بر مشتق دوم r تأثیر میگذارد. با این حال، ما این سهم را نادیده میگیریم. معادله لاگرانژی حرکت توپ به صورت زیر ارائه میشود:
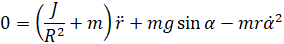
خطیسازی این معادله حول زاویه پرتو، آلفا = ۰، تقریب خطی زیر را از سیستم به ما میدهد:
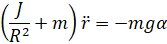
معادلهای که زاویه پرتو را به زاویه چرخدنده مرتبط میکند، میتواند با معادله زیر به صورت خطی تقریب زده شود:
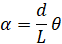
با جایگذاری این در معادله قبلی، داریم:
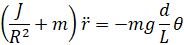
۱. تابع تبدیل:
با گرفتن تبدیل لاپلاس از معادله بالا، معادله زیر بدست میآید:
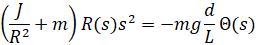
با مرتبسازی مجدد، تابع انتقال را از زاویه چرخدنده (Theta(s)) به موقعیت گوی (R(s)) مییابیم.
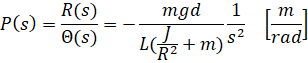
لازم به ذکر است که تابع تبدیل نیروگاه فوق یک انتگرالگیر دوگانه است. به همین دلیل، پایداری کمی دارد و یک مسئله کنترل چالشبرانگیز را ایجاد خواهد کرد.
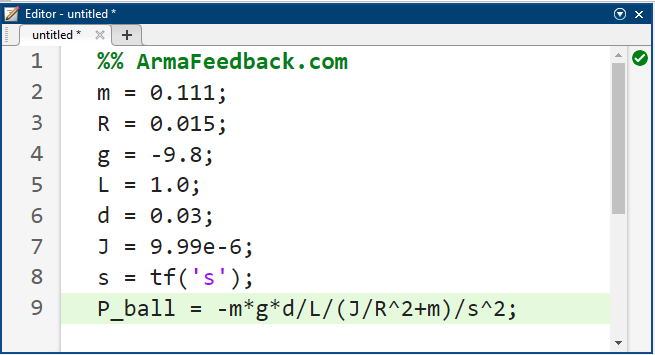
تابع تبدیل را میتوان در متلب به صورت زیر پیادهسازی کرد:
کد متلب:
۲. فضای حالت:
معادلات سیستم خطیشده را میتوان به شکل فضای حالت نیز نمایش داد. این کار را میتوان با انتخاب موقعیت توپ (r) و سرعت (r) به عنوان متغیر حالت و زاویه چرخدنده (θ) به عنوان ورودی انجام داد. نمایش فضای حالت در زیر نشان داده شده است:
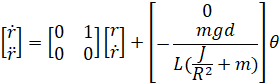
با این حال، برای مثال فضای حالت خود، از مدلی کمی متفاوت استفاده خواهیم کرد. همان معادله برای توپ همچنان اعمال میشود، اما به جای کنترل موقعیت از طریق زاویه چرخدنده، تتا، گشتاور اعمال شده به تیر را مستقیماً کنترل خواهیم کرد. در زیر نمایش این سیستم آمده است:
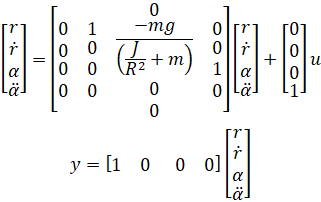
نکته: برای این سیستم از چرخ دنده و بازوی اهرمی استفاده نمیشود، در عوض یک موتور در مرکز تیر، گشتاور را به تیر اعمال میکند تا موقعیت گوی را کنترل کند.
معادلات فضای حالت را میتوان در متلب با دستورات زیر نمایش داد (این معادلات برای مدل کنترل گشتاور هستند).
کد متلب:
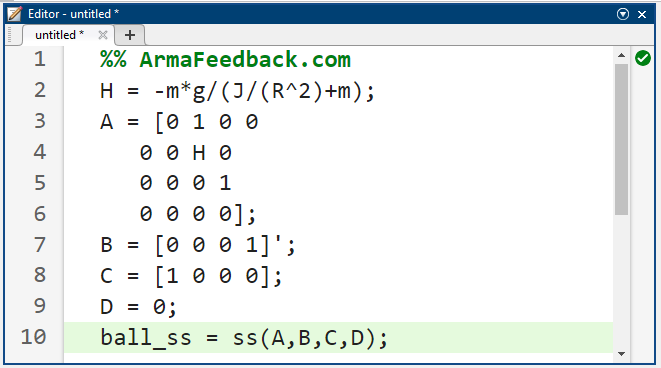
تحلیل پایداری سیستم مورد مطالعه:
نمایش قطب و صفر سیستم:
سیستم گوی و میله یک سیستم نوع دوم است که در مبدا دو قطب دارد، همانطور که در نقشه قطب/صفر زیر مشاهده میشود. از آنجایی که قطبها دقیقاً در نیم صفحه چپ نیستند، سیستم حلقه باز همانطور که در پاسخ پله زیر مشاهده میشود، ناپایدار خواهد بود.
کد متلب:

نتیجه شبیهسازی:
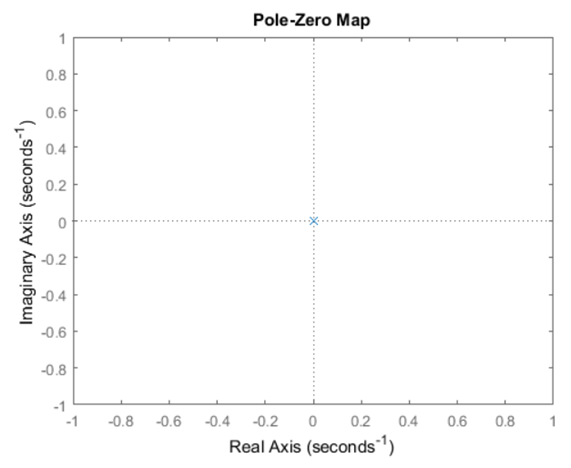
پاسخ پله حلقه باز
حال، میخواهیم پاسخ توپ را به ورودی پله روی زاویه چرخدنده سروو موتور (تتا) (پله ۱ رادیان) مشاهده کنیم. برای انجام این کار، باید خط زیر را به فایل m خود اضافه کنید.
کد متلب:

نتیجه شبیهسازی:
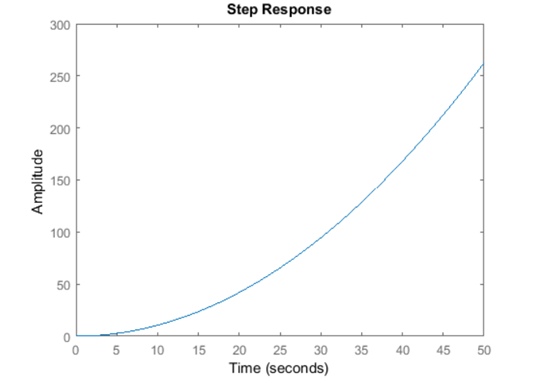
از این نمودار مشخص است که سیستم در حالت حلقه باز ناپایدار است و باعث میشود توپ از انتهای تیر به بیرون بغلتد. بنابراین، به روشی برای کنترل موقعیت توپ در این سیستم نیاز است. چندین مثال از طراحی کنترلکننده در این آموزشها برای رفع این مشکل ارائه شده است.
نمایش فضای حالت مثال گوی و تیر در زیر آمده است:
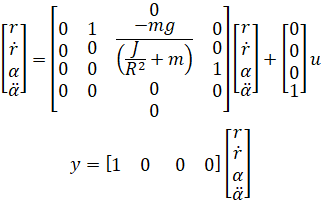
برخلاف مثالهای قبلی که برای کنترل تیر و گوی، زاویه چرخدنده را کنترل میکردیم، در اینجا ما ddot alpha را کنترل میکنیم. با انجام این کار، اساساً گشتاور اعمال شده در مرکز تیر توسط یک موتور را کنترل میکنیم. بنابراین، به سیستم چرخدنده و اهرم نیازی نداریم.
معیارهای طراحی برای این مسئله عبارتند از:
زمان نشست کمتر از ۳ ثانیه
فراجهش کمتر از ۵٪
کنترلکننده فیدبک حالت کامل (Full State Feedback)
ما برای این سیستم فیزیکی، کنترلکنندهای طراحی خواهیم کرد که از کنترل فیدبک حالت کامل استفاده میکند. شماتیکی از این نوع سیستم در زیر نشان داده شده است:
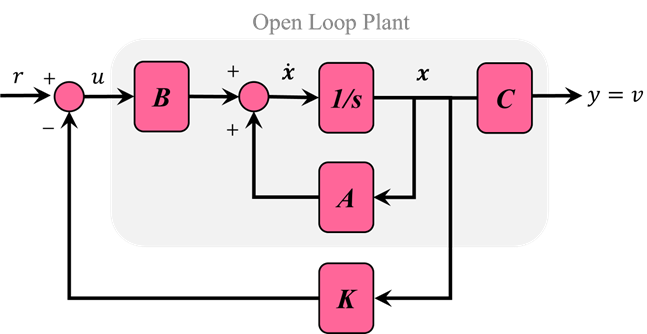
به یاد داشته باشید که چندجملهای مشخصه برای این سیستم حلقه بسته، دترمینان sI-(A-BK) است، که در آن s متغیر لاپلاس است. برای سیستم ما، ماتریسهای A و BK هر دو 4x4 هستند. از این رو، باید چهار قطب برای سیستم ما وجود داشته باشد. در طراحی کنترلکننده فیدبک حالت کامل، میتوانیم این قطبها را به هر جایی که میخواهیم منتقل کنیم.
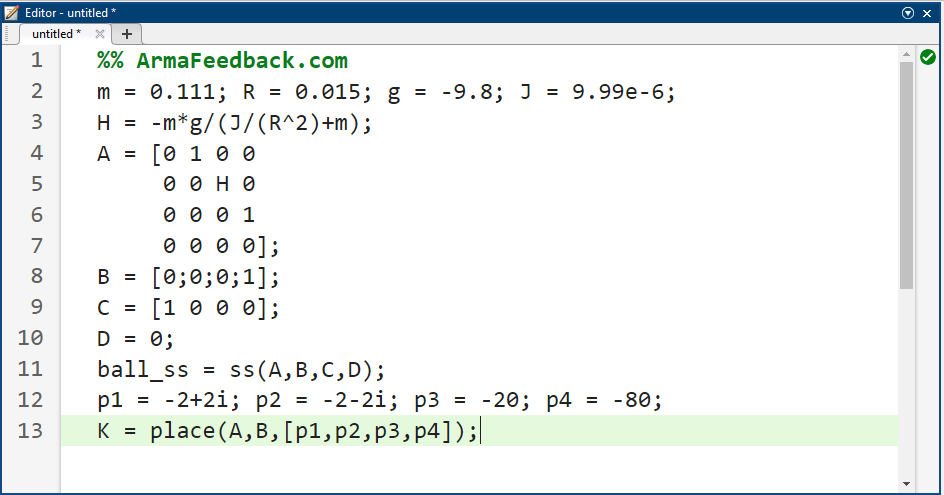
برای طراحی ما، فراجهش کمتر از ۵٪ مورد نظر است که معادل زتای ۰.۷ است (لطفاً برای رابطه بین فراجهش و نسبت میرایی به کتاب درسی خود مراجعه کنید). در مکان هندسی ریشهها، این معیار به صورت یک خط ۴۵ درجه که از مبدا شروع شده و به سمت صفحه نیمه چپ امتداد مییابد، نمایش داده میشود. ما میخواهیم قطبهای مورد نظر خود را روی یا زیر این خط قرار دهیم. معیار بعدی ما زمان نشست کمتر از ۳ ثانیه است که معادل sigma = 4.6 / Ts = 4.6 / 3 = 1.53 است که با یک خط عمودی در -۱.۵۳ روی مکان هندسی ریشهها نمایش داده میشود. هر چیزی فراتر از این خط در صفحه نیمه چپ، مکان مناسبی برای قطبهای ما است. بنابراین قطبهای خود را در -۲+۲i و -۲-۲i قرار میدهیم. فعلاً قطبهای دیگر را در سمت چپ قرار میدهیم تا تأثیر زیادی بر پاسخ نداشته باشند. برای شروع، آنها را در -۲۰ و -۸۰ قرار دهید. حالا که قطبهایمان را داریم، میتوانیم با استفاده از دستور place در متلب، کنترلر (ماتریس K) را پیدا کنیم. کد زیر را در یک m-file کپی کنید تا سیستم را مدلسازی کرده و ماتریس K را پیدا کنید:
کد متلب:
پس از اضافه کردن ماتریس K، معادلات فضای حالت اکنون به صورت زیر در میآیند:
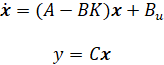
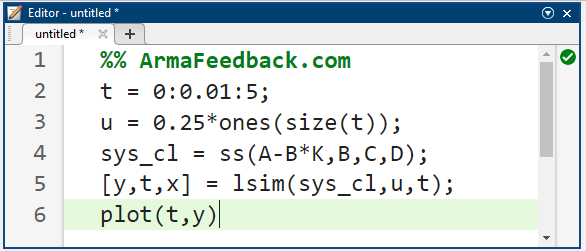
اکنون میتوانیم پاسخ حلقه بسته به ورودی با پله 0.25 متر را با استفاده از دستور lsim شبیهسازی کنیم. موارد زیر را به m-file خود اضافه کنید. m-file خود را اجرا کنید و باید نمودار زیر را دریافت کنید:
کد متلب:
نتیجه شبیهسازی:
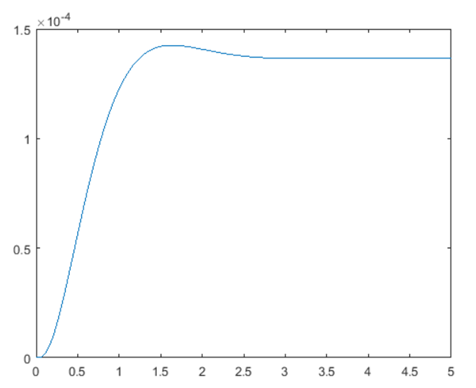
از این نمودار میبینیم که یک خطای حالت پایدار بزرگ وجود دارد، برای جبران این خطا، باید یک جبران ورودی مرجع اضافه کنیم (که در بخش بعدی توضیح داده شده است). با این حال، معیارهای زمان فراجهش و زمان نشست برآورده میشوند. اگر میخواستیم فراجهش را بیشتر کاهش دهیم، میتوانستیم قسمت موهومی قطب را کوچکتر از قسمت واقعی کنیم. همچنین، اگر زمان نشست سریعتری میخواستیم، قطبها را در صفحه نیمه چپ بیشتر جابجا میکردیم. برای دیدن این روندها، میتوانید با موقعیت قطبها آزمایش کنید.
ورودی مرجع:
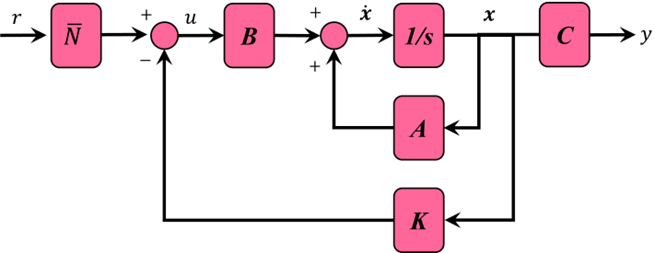
حالا میخواهیم از شر خطای حالت پایدار خلاص شویم. برخلاف سایر روشهای طراحی که در آنها خروجی را فیدبک میکنیم و آن را با ورودی مرجع مقایسه میکنیم تا خطا را محاسبه کنیم، با یک کنترلکننده فیدبک حالت کامل، هر دو حالت را فیدبک میدهیم. باید مقدار حالت پایدار حالتها را محاسبه کنیم، آن را در بهره انتخاب شده K ضرب کنیم و از یک مقدار جدید به عنوان مرجع برای محاسبه ورودی استفاده کنیم. این کار را میتوان با اضافه کردن یک خط بهره ثابت روی N بعد از مرجع انجام داد. شماتیک زیر این رابطه را نشان میدهد:
overline N را میتوان با استفاده از تابع تعریفشده توسط کاربر rscale.m پیدا کرد. آن را از اینجا، rscale.m، دانلود کنید و در دایرکتوری که m-file شما در آن قرار دارد قرار دهید. کد زیر را در m-file خود کپی کنید و آن را اجرا کنید تا پاسخ مرحله را با overlineN اضافه شده مشاهده کنید.
کد متلب:
نتیجه شبیهسازی:
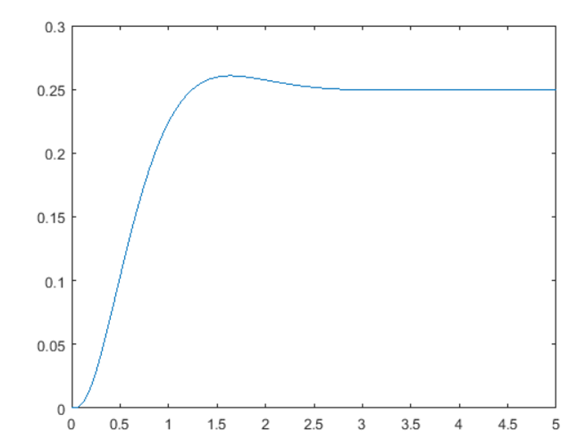
اکنون خطای حالت ماندگار حذف شده و تمام معیارهای طراحی برآورده شدهاند.
نکته: یک مسئله طراحی لزوماً یک پاسخ منحصر به فرد ندارد. استفاده از این روش (یا هر روش دیگری) ممکن است منجر به جبرانکنندههای مختلف زیادی شود. برای تمرین، میتوانید به عقب برگردید و سعی کنید موقعیت قطبها را تغییر دهید تا ببینید سیستم چگونه پاسخ میدهد.
منابع:
C. H. Houpis, S. N. Sheldon, and J. J. D'Azzo, Linear Control System Analysis and Design, 5th ed. Boca Raton, FL: CRC Press, 2013
Y. Bavafa-Toosi, Introduction to Linear Control Systems. Amsterdam, Netherlands: Elsevier, 2017
K. Ogata, Modern Control Engineering, 5th ed. Upper Saddle River, NJ: Pearson, 2010
N. S. Nise, Control Systems Engineering, 6th ed. Hoboken, NJ: John Wiley & Sons, 2011
C.-T. Chen, Linear System Theory and Design, 3rd ed. New York, NY: Oxford University Press, 1999
G. F. Franklin, J. D. Powell, and A. Emami-Naeini, Feedback Control of Dynamic Systems, 7th ed. Boston, MA: Pearson, 2014
#کنترل_خطی #کنترل_مدرن #کنترل_مقاوم #کنترل_فازی #کنترل_کنترل_هوشمند #کنترل_دیجیتال #کنترل_پیش_بین_مبتنی_بر_مدل #کنترل_بهینه #کنترل_چند_متغییره #کنترل_کلاسیک #کنترل_اتوماتیک #کنترل_عصبی #کنترل_چند_عاملی #کنترل_شبکهای #کنترل_تطبیقی #کنترل #کنترل_غیر_خطی #مهندسی_کنترل #متلب #سیمولینک#متلب_سیمولینک #تابع_تبدیل #معادلات_حالت #مدل_سازی #شبیهسازی #کنترل_مبتنی_بر_داده #کنترل_سیستم #سیستم #بهینه_سازی #سنسور #فیدبک #بازخورد#طراحی