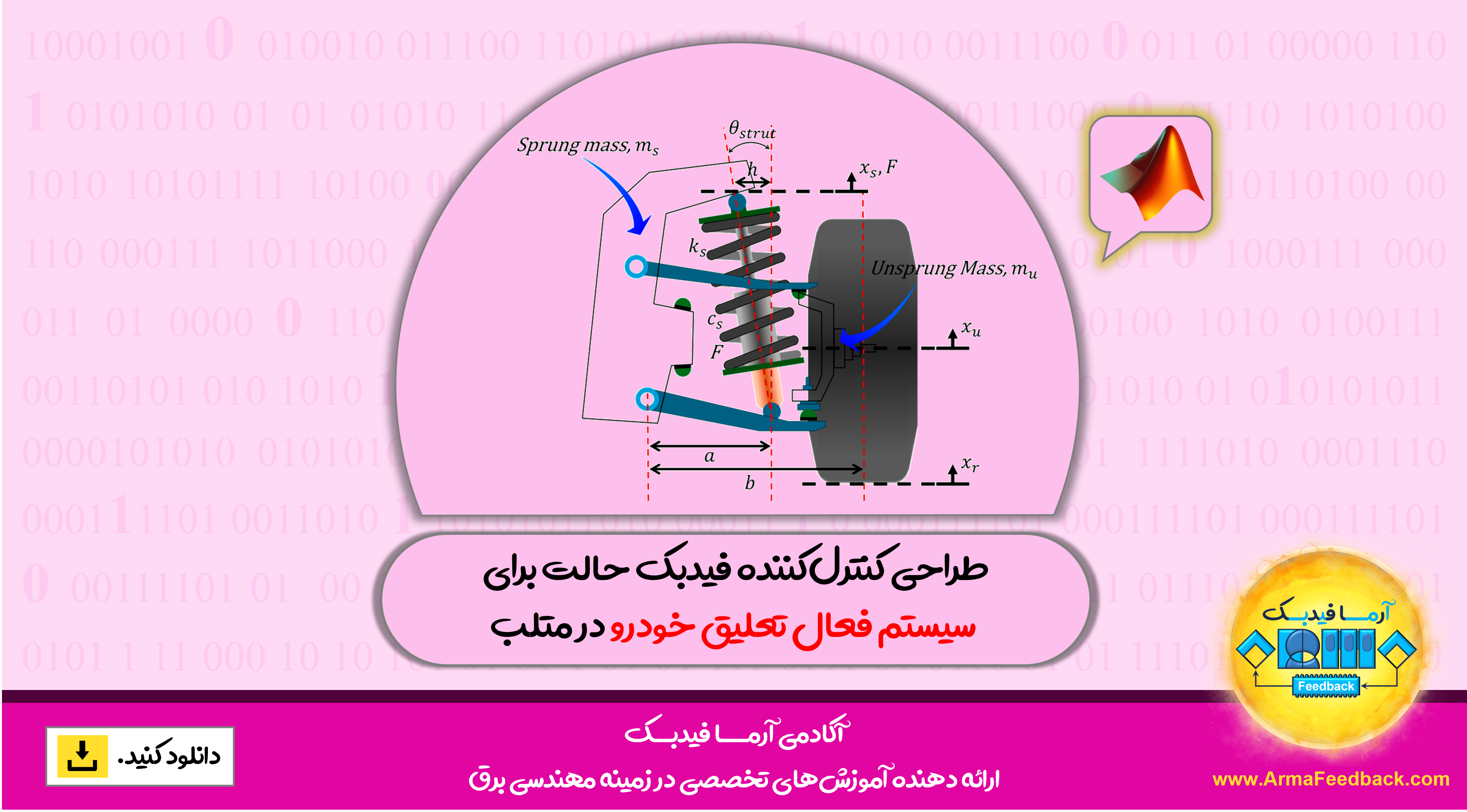
طراحی کنترلکننده فیدبک حالت برای سیستم فعال تعلیق خودرو در متلب
فهرست مطالب
- 1) روابط حاکم
2) پارامترهای سیستم
3) معادلات حرکت
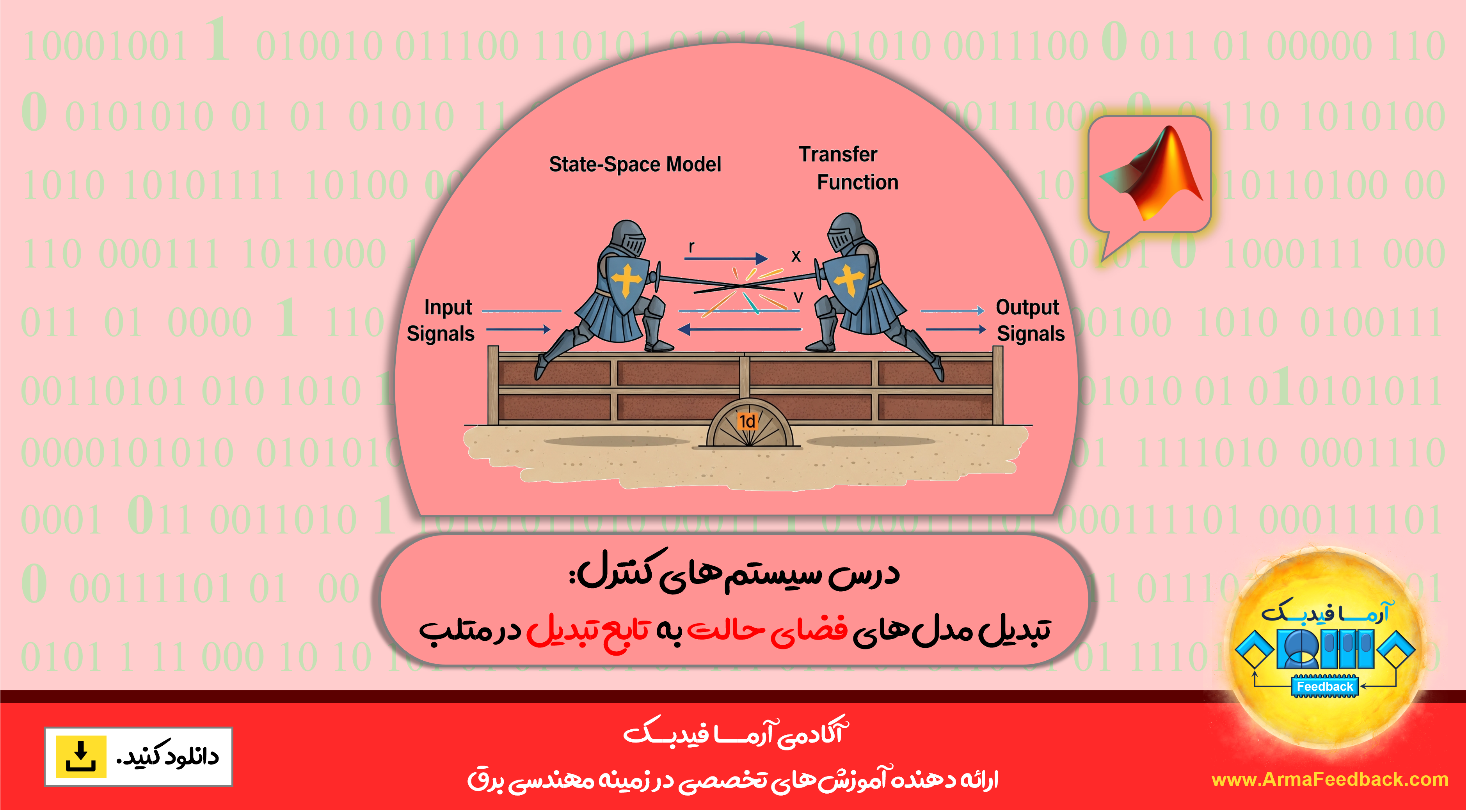
4) مدلهای تابع انتقال
5) وارد کردن معادلات در متلب
6) مدل سیستم
7) پارامترهای سیستم
8) الزامات طراحی
9) پاسخ پله حلقه باز
10) طراحی کنترلکننده فیدبک حالت کامل بهینه
11) ترسیم پاسخ حلقه بسته
12) منابع
روابط حاکم
طراحی سیستم تعلیق خودرو یک مسئله کنترلی جالب و چالشبرانگیز است. هنگام طراحی سیستم تعلیق، از یک مدل ۱/۴ (یکی از چهار چرخ) برای سادهسازی مسئله به یک سیستم فنر-دمپر چندگانه ۱ بعدی استفاده میشود. نموداری از این سیستم در زیر نشان داده شده است. این مدل برای یک سیستم تعلیق فعال است که در آن یک محرک گنجانده شده است که قادر به تولید نیروی کنترلی U برای کنترل حرکت بدنه اتوبوس است.
تصویر سیستم تعلیق یک چهارم خودرو و مدل تعلیق پارامتر فشرده:
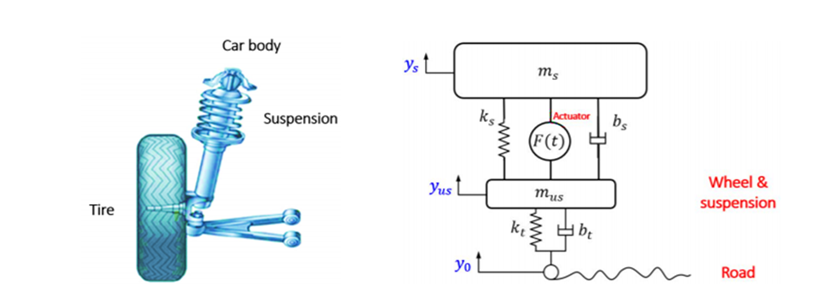
پارامترهای و کمیت های سیستم مورد مطالعه عبارتند از:
(M1) جرم بدنه اتوبوس ¼ 2500 کیلوگرم
(M2) جرم سیستم تعلیق 320 کیلوگرم
(K1) ثابت فنر سیستم تعلیق 80,000 نیوتن بر متر
(K2) ثابت فنر چرخ و تایر 500,000 نیوتن بر متر
(b1) ثابت میرایی سیستم تعلیق 350 نیوتن بر ثانیه
(b2) ثابت میرایی چرخ و تایر 15,020 نیوتن بر متر
(U) نیروی کنترل
معادلات حرکت
از تصویر بالا و قانون نیوتن، میتوانیم معادلات دینامیکی را به صورت زیر بدست آوریم:
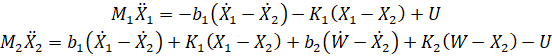
مدلهای تابع انتقال سیستم:
فرض کنید که تمام شرایط اولیه صفر هستند، به طوری که این معادلات نشاندهنده وضعیتی هستند که چرخ خودرو از یک دستانداز بالا میرود. معادلات دینامیکی فوق را میتوان با استفاده از تبدیل لاپلاس به شکل توابع انتقال بیان کرد. مشتق خاص از معادلات فوق به توابع انتقال G1(s) و G2(s) در زیر نشان داده شده است که در آن هر تابع انتقال به ترتیب دارای خروجی X1-X2 و ورودیهای U و W است.
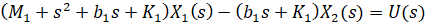
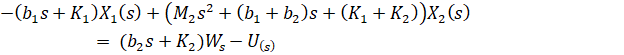
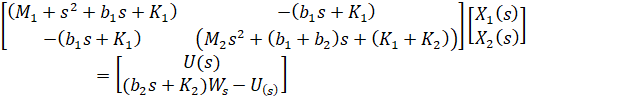
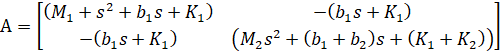
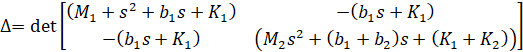
یا
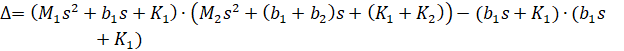
معکوس ماتریس A را بیابید و سپس آن را در ورودیهای U(s) و W(s) در سمت راست به صورت زیر ضرب کنید:
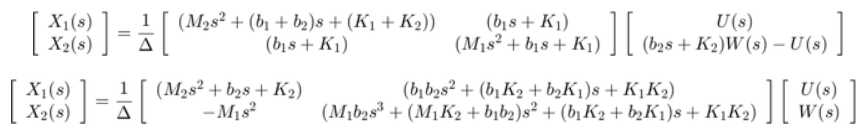
وقتی میخواهیم فقط ورودی کنترلی U(s) را در نظر بگیریم، W(s) را برابر با ۰ قرار میدهیم. بنابراین تابع تبدیل G1(s) به صورت زیر خواهد بود:
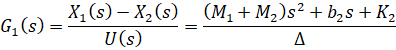
وقتی میخواهیم فقط ورودی اختلال W(s) را در نظر بگیریم، U(s) را برابر با ۰ قرار میدهیم. بنابراین تابع تبدیل G2(s) را به صورت زیر بدست میآوریم:
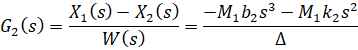
وارد کردن معادلات در متلب:
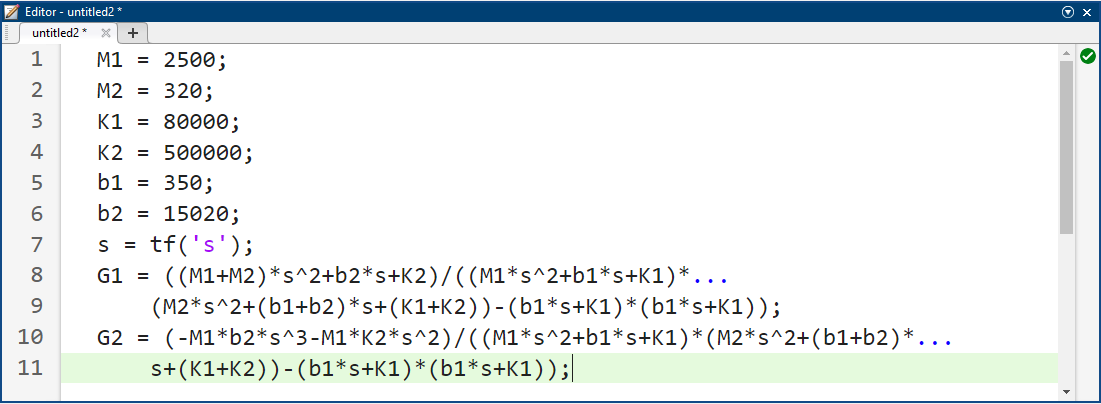
ما میتوانیم مدلهای تابع تبدیل فوق را در متلب با وارد کردن دستورات زیر در پنجره فرمان متلب تولید کنیم.
کد متلب:
الزامات طراحی
یک سیستم تعلیق خوب اتوبوس باید از توانایی مطلوبی برای حفظ تعادل در جاده برخوردار باشد، ضمن اینکه هنگام عبور از دستاندازها و چالههای جاده، راحتی را نیز فراهم کند. هنگامی که اتوبوس هرگونه اختلال جادهای (مانند چالهها، ترکها و آسفالت ناهموار) را تجربه میکند، بدنه اتوبوس نباید نوسانات زیادی داشته باشد و این نوسانات باید به سرعت از بین بروند. از آنجایی که اندازهگیری فاصله X1-W بسیار دشوار است و تغییر شکل لاستیک (X2-W) ناچیز است، ما از فاصله X1-X2 به جای X1-W به عنوان خروجی در مسئله خود استفاده خواهیم کرد. به خاطر داشته باشید که این یک تقریب است.
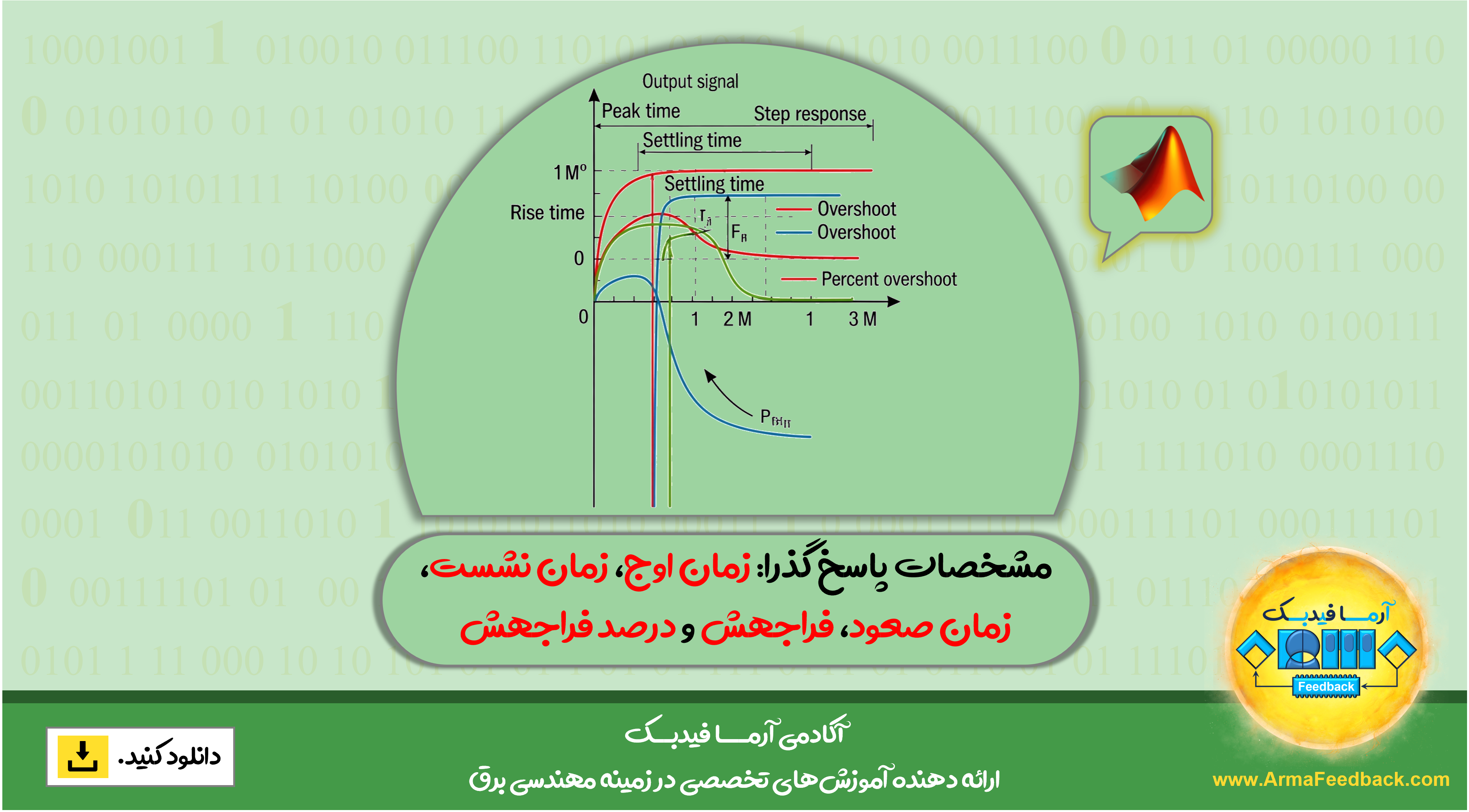
اختلال جاده (W) در این مسئله با یک ورودی پلهای شبیهسازی میشود. این پله میتواند نشاندهنده خروج اتوبوس از چاله باشد. ما میخواهیم یک کنترلکننده بازخورد طراحی کنیم تا خروجی (X1-X2) دارای جهش کمتر از 5٪ و زمان نشست کوتاهتر از 5 ثانیه باشد. برای مثال، وقتی اتوبوس روی یک پله ۱۰ سانتیمتری حرکت میکند، بدنه اتوبوس در محدوده +/- ۵ میلیمتر نوسان میکند و ظرف ۵ ثانیه به حالت اولیه خود برمیگردد.
پاسخ پله حلقه باز سیستم مورد مطالعه:
ما میتوانیم از متلب برای نمایش عملکرد سیستم حلقه باز اصلی (بدون هیچ کنترل فیدبکی) استفاده کنیم. دستورات زیر را به m-file اضافه کنید و آن را در پنجره فرمان متلب اجرا کنید تا پاسخ ورودی نیروی محرک پله واحد، U(s) را ببینید. توجه داشته باشید که دستور پله، ورودیهای پله واحد را برای هر ورودی تولید میکند.
کد متلب:
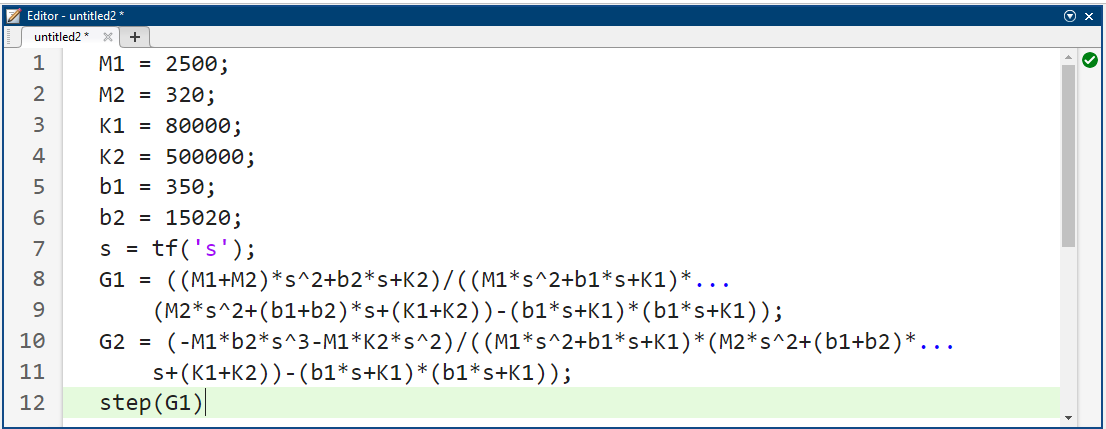
نتیجه شبیهسازی:
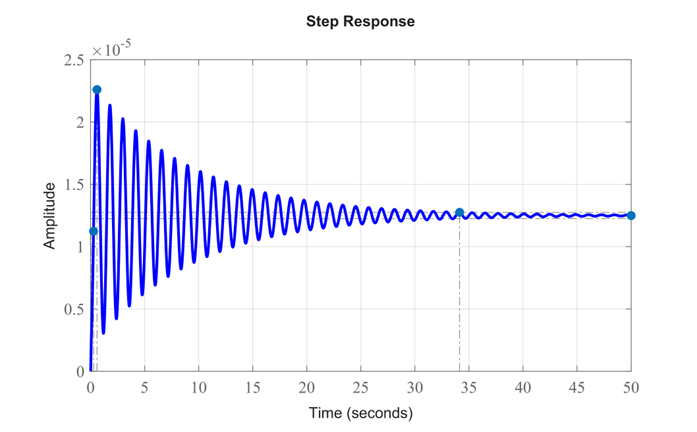
از این نمودار پاسخ حلقه باز برای نیروی محرک پله واحد، میتوانیم ببینیم که سیستم تحت میرایی ضعیف است. افرادی که در اتوبوس نشسته اند، مقدار بسیار کمی نوسان را احساس خواهند کرد. علاوه بر این، اتوبوس برای رسیدن به حالت پایدار به زمان غیرقابل قبولی نیاز دارد (زمان نشست بسیار زیاد است). اکنون دستورات زیر را وارد کنید تا پاسخ را برای ورودی اختلال پله، W(s)، با بزرگی 0.1 متر مشاهده کنید.
کد متلب:
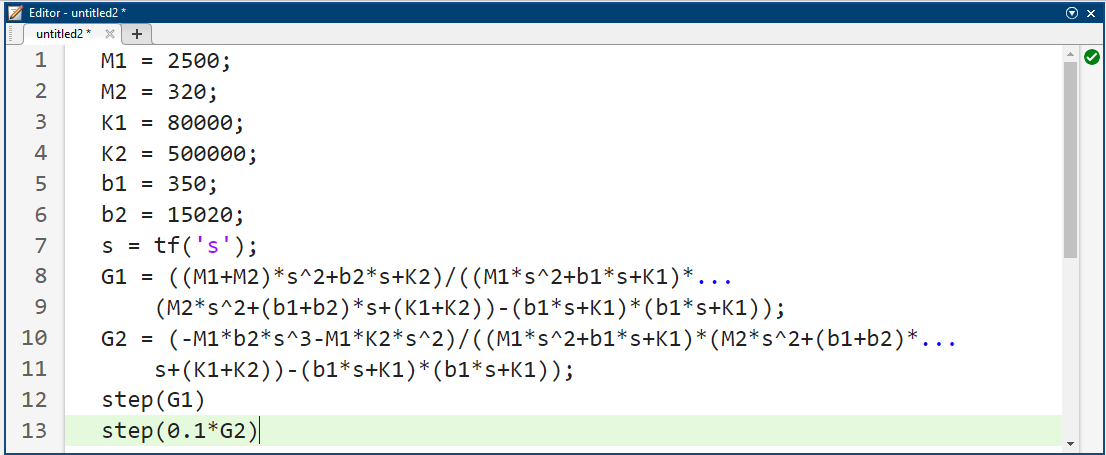
نتیجه شبیهسازی:
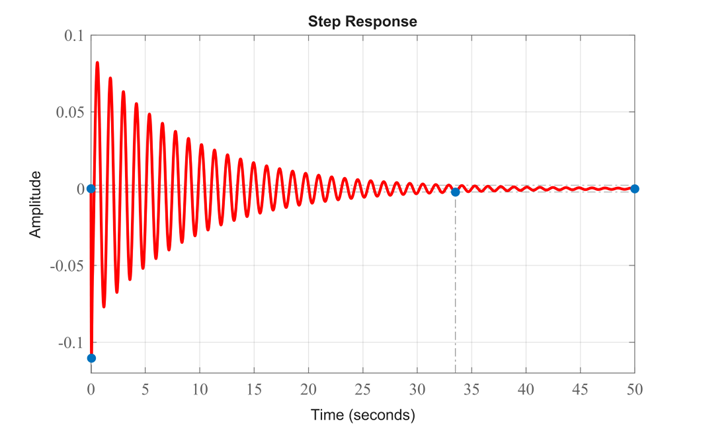
از این نمودار پاسخ حلقه باز برای اغتشاش پلهای ۱۰ سانتیمتری، میتوانیم ببینیم که وقتی اتوبوس از یک دستانداز ۱۰ سانتیمتری در جاده عبور میکند، بدنه اتوبوس برای مدت زمان غیرقابل قبولی (حدود ۵۰ ثانیه) با دامنه اولیه ۸ سانتیمتر نوسان میکند. افرادی که در اتوبوس نشستهاند به دلیل فراجهش زیاد و زمان طولانی نشست، با چنین نوسانی راحت نخواهند بود.
راه حل این مشکلات، اضافه کردن یک کنترلکننده فیدبک به سیستم برای بهبود عملکرد است. شماتیک سیستم حلقه بسته به صورت زیر است که در بخشهای طراحی کنترلکننده با جزئیات بیشتری مورد بحث قرار خواهد گرفت.
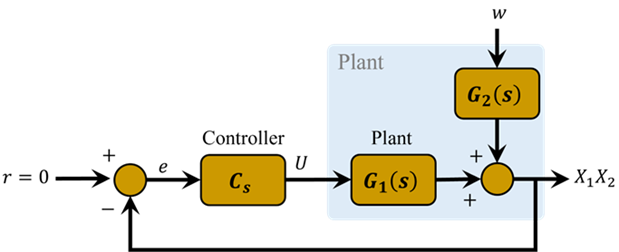
پیاده سازی کنترلر بر مبنای معادلات حالات
از مسئله اصلی، معادلات دینامیکی در فرم فضای حالت به صورت زیر هستند که در آن Y1 = X1 - X2 است.

ما میخواهیم یک کنترلکننده فیدبک طراحی کنیم تا وقتی اغتشاش جاده (W) توسط ورودی پله واحد شبیهسازی میشود، خروجی (X1-X2) زمان نشست کمتر از 5 ثانیه و فراجهش کمتر از 5% داشته باشد. به عنوان مثال، وقتی اتوبوس روی یک پله 10 سانتیمتری حرکت میکند، بدنه اتوبوس در محدوده +/- 5 میلیمتر نوسان میکند و نوسان آن ظرف 5 ثانیه متوقف میشود.
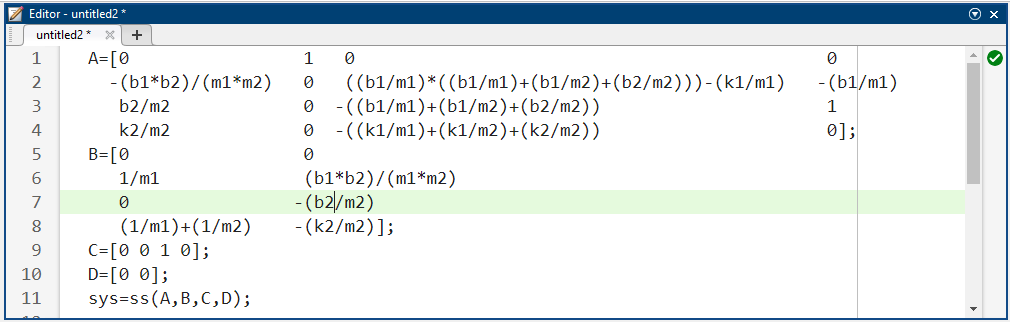
مدل سیستم را میتوان با ایجاد یک m-file جدید و وارد کردن دستورات زیر در MATLAB نمایش داد (برای جزئیات دریافت این دستورات به مسئله اصلی مراجعه کنید). ما باید ماتریسهای A، B، C و D را با وارد کردن موارد زیر در m-file تعریف کنیم:
کد متلب:
طراحی کنترلکننده فیدبک حالت کامل بهینه
ابتدا، بیایید یک کنترلکننده فیدبک حالت کامل برای سیستم طراحی کنیم. فعلاً با فرض اینکه همه حالتها قابل اندازهگیری هستند (این فرض احتمالاً درست نیست اما برای این مسئله کافی است)، شماتیک سیستم در زیر نشان داده شده است.
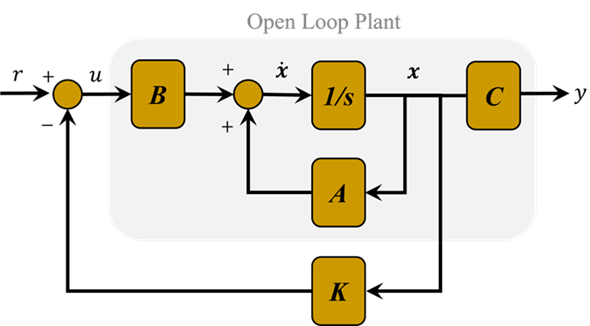
چندجملهای مشخصه برای این سیستم حلقه بسته، دترمینان (sI-(A-B[1,0]'K)) است. توجه داشته باشید که این چندجملهای sI-(A-BK) نیست، زیرا کنترلکننده K فقط میتواند نیروی ورودی u را کنترل کند، اما نمیتواند اغتشاش جاده W را کنترل کند. به یاد داشته باشید که ماتریس B ما یک ماتریس 4 در 2 است و ما فقط به ستون اول B برای کنترل U نیاز داریم.
برای این مثال، ما باید از عمل انتگرالی برای رسیدن به خطای حالت پایدار صفر استفاده کنیم، بنابراین یک حالت اضافی اضافه میکنیم که عبارت است از int(X1-X2) = int(Y1). در واقعیت، گذرگاه در نهایت به تعادلی میرسد که خطای حالت پایدار صفر را به همراه دارد. حالتهای جدید X1، X1_dot، Y1، Y1_dot و Y2 هستند. همچنین ماتریسهای فضای حالت، A، B و C، پس از اضافه شدن حالت جدید به صورت زیر در میآیند.
کد متلب:
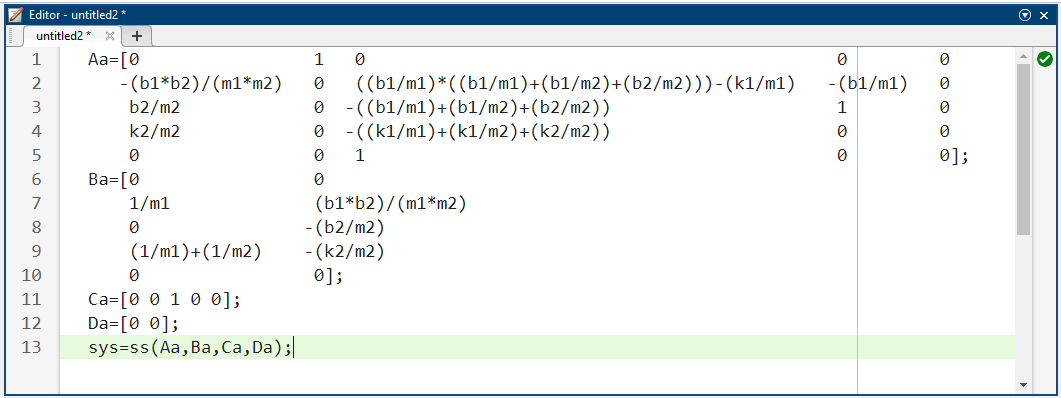
در واقع، یک میانبر برای متلب وجود دارد تا به همین نتیجه برسد.
کد متلب:

کد متلب فوق را به m-file اضافه کنید. در این حالت، ما با مسئله مانند طراحی یک کنترلکننده PID برخورد میکنیم. کنترل انتگرالی از حالت جدید به دست میآید. کنترل تناسبی از بهره روی Y1 یا X1-X2 به دست میآید. کنترل مشتق مستقیم خروجی امکانپذیر نیست، زیرا مشتق Y1 یا X1-X2 یک حالت نیست. در عوض، ما از مشتق X1 استفاده میکنیم که برای بازخورد در دسترس است. (در حالی که اندازهگیری X1 ممکن است دشوار باشد، X1_dot را میتوان با انتگرالگیری از خروجی یک شتابسنج نصب شده روی باس به دست آورد.) این شبیه به اضافه کردن میرایی بیشتر به سرعت نوسان سیستم تعلیق باس است. کد متلب زیر را برای کنترلکننده K در m-file اضافه کنید:
کد متلب:
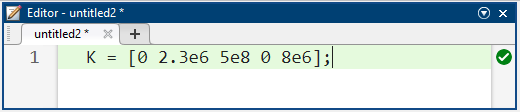
ما با آزمون و خطا به این مقدار ماتریس K رسیدیم و همانطور که قبلاً گفته شد، بهره مشتق X1، Y1 و انتگرال Y1 را تنظیم کردیم.
رسم نمودار پاسخ حلقه بسته در متلب
با نگاهی دوباره به شماتیک بالا، میبینیم که پس از اضافه کردن ماتریس K به سیستم، معادلات فضای حالت به صورت زیر در میآیند:
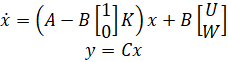
اکنون میتوانیم پاسخ حلقه بسته را با اضافه کردن کد زیر به m-file بدست آوریم. توجه داشته باشید که برای شبیهسازی اغتشاش پلهای با ارتفاع 0.1 متر، باید ماتریس B را در 0.1 ضرب کنیم.
کد متلب:
نتیجه شبیهسازی:
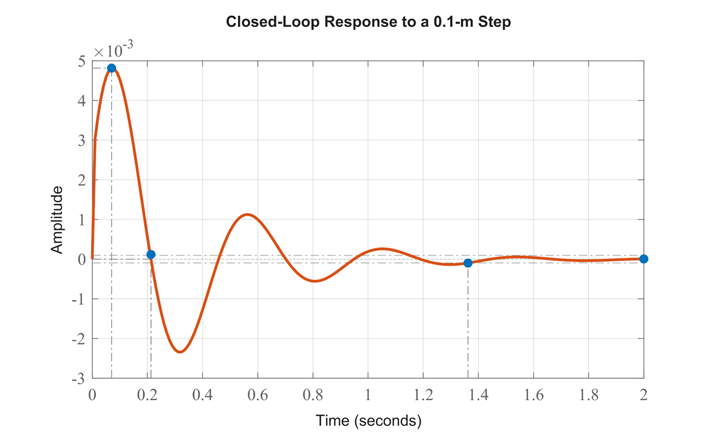
از روی نمودار میبینیم که الزامات درصد فراجهش و زمان نشست برآورده شدهاند. علاوه بر این، خطای حالت پایدار نیز به صفر نزدیک میشود. بنابراین، نتیجه میگیریم که پاسخ رضایتبخش است. میتوانید با بهره ماتریس K بازی کنید.
منابع:
C. H. Houpis, S. N. Sheldon, and J. J. D'Azzo, Linear Control System Analysis and Design, 5th ed. Boca Raton, FL: CRC Press, 2013
Y. Bavafa-Toosi, Introduction to Linear Control Systems. Amsterdam, Netherlands: Elsevier, 2017
K. Ogata, Modern Control Engineering, 5th ed. Upper Saddle River, NJ: Pearson, 2010
N. S. Nise, Control Systems Engineering, 6th ed. Hoboken, NJ: John Wiley & Sons, 2011
C.-T. Chen, Linear System Theory and Design, 3rd ed. New York, NY: Oxford University Press, 1999
G. F. Franklin, J. D. Powell, and A. Emami-Naeini, Feedback Control of Dynamic Systems, 7th ed. Boston, MA: Pearson, 2014
#کنترل_خطی #کنترل_مدرن #کنترل_مقاوم #کنترل_فازی #کنترل_کنترل_هوشمند #کنترل_دیجیتال #کنترل_پیش_بین_مبتنی_بر_مدل #کنترل_بهینه #کنترل_چند_متغییره #کنترل_کلاسیک #کنترل_اتوماتیک #کنترل_عصبی #کنترل_چند_عاملی #کنترل_شبکهای #کنترل_تطبیقی #کنترل #کنترل_غیر_خطی #مهندسی_کنترل #متلب #سیمولینک#متلب_سیمولینک #تابع_تبدیل #معادلات_حالت #مدل_سازی #شبیهسازی #کنترل_مبتنی_بر_داده #کنترل_سیستم #سیستم #بهینه_سازی #سنسور #فیدبک #بازخورد