طراحی کنترلکننده فیدبک حالت برای سیستم کروز کنترل خودروها در متلب
چکیده مطالب:
این مقاله، مدلسازی و طراحی کنترلکننده برای یک سیستم کروز کنترل خودرو را شرح میدهد. هدف اصلی، حفظ سرعت ثابت خودرو در برابر اختلالات خارجی است. ابتدا یک مدل ساده از دینامیک خودرو (جرم-میراگر) با استفاده از معادلات دیفرانسیل، فضای حالت و تابع تبدیل ارائه میشود. سپس، با توجه به الزامات طراحی، یک کنترلکننده با استفاده از تکنیک جایگذاری قطب طراحی میگردد. برای رفع مشکل خطای حالت ماندگار، از ضریب مقیاسبندی ورودی مرجع (Nbar) بهره گرفته میشود که در نهایت منجر به برآورده شدن تمامی الزامات طراحی میگردد.
فهرست مطالب:
مدلسازی سیستم:
- 1) تنظیمات فیزیکی
- 2) معادلات سیستم
- 3) پارامترهای سیستم
- 4) مدل فضای حالت
- 5) مدل تابع تبدیل
طراحی کنترلر:
- 6) معادلات فضای حالت
- 7) الزامات طراحی
- 8) طراحی کنترل با استفاده از جایگذاری قطب
- 9) ورودی مرجع
- 10) منابع
روابط حاکم:
کروز کنترل اتوماتیک نمونهای عالی از یک سیستم کنترل بازخوردی است که در بسیاری از خودروهای مدرن یافت میشود. هدف سیستم کروز کنترل، حفظ سرعت ثابت خودرو علیرغم اختلالات خارجی، مانند تغییرات باد یا شیب جاده است. این کار با اندازهگیری سرعت خودرو، مقایسه آن با سرعت مطلوب یا مرجع و تنظیم خودکار دریچه گاز طبق یک قانون کنترل انجام میشود.

در اینجا یک مدل ساده از دینامیک خودرو را که در نمودار جسم آزاد (FBD) بالا نشان داده شده است، در نظر میگیریم. نیروی کنترلی u بر خودرو اعمال میشود. نیروی u نشان دهنده نیروی تولید شده در سطح مشترک جاده/لاستیک است. برای این مدل ساده شده، فرض میکنیم که میتوانیم این نیرو را مستقیماً کنترل کنیم و از دینامیک سیستم انتقال قدرت، لاستیکها و غیره که در تولید نیرو نقش دارند، صرف نظر میکنیم. فرض میشود نیروهای مقاوم، bv، ناشی از مقاومت غلتشی و نیروی باد، به صورت خطی با سرعت خودرو، v، تغییر میکنند و در جهت مخالف حرکت خودرو عمل میکنند.
معادلات سیستم:
با این فرضیات، یک سیستم جرم-میراگر مرتبه اول باقی میماند. با جمع نیروها در جهت x و اعمال قانون دوم نیوتن، به معادله سیستم زیر میرسیم:
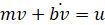
از آنجایی که ما به کنترل سرعت وسیله نقلیه علاقهمند هستیم، معادله خروجی به صورت زیر انتخاب میشود:
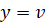
پارامترهای سیستم:
برای این مثال، فرض کنید پارامترهای سیستم عبارتند از:
جرم خودرو ۱۰۰۰ کیلوگرم (m)
ضریب میرایی ۵۰ نیوتن بر ثانیه (b)
مدل فضای حالت:
سیستمهای مرتبه اول فقط یک حالت ذخیرهسازی انرژی دارند، در این مورد انرژی جنبشی خودرو، و بنابراین فقط به یک متغیر حالت، یعنی سرعت، نیاز است. بنابراین نمایش فضای حالت به صورت زیر است:
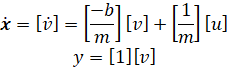
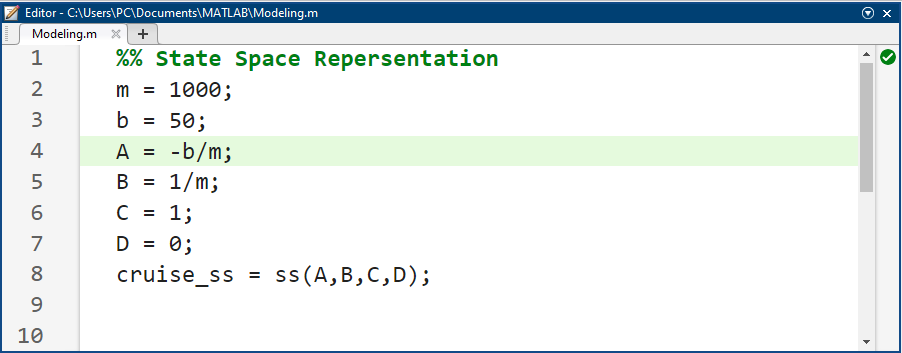
ما این مدل فضای حالت را با استفاده از دستورات زیر وارد متلب میکنیم:
کد متلب:
مدل تابع تبدیل:
با در نظر گرفتن تبدیل لاپلاس معادله دیفرانسیل حاکم و با فرض شرایط اولیه صفر، تابع انتقال سیستم کروز کنترل به صورت زیر بدست میآید:
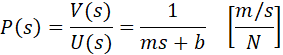
مدل تابع تبدیل را با استفاده از دستورات زیر وارد متلب میکنیم:
کد متلب:
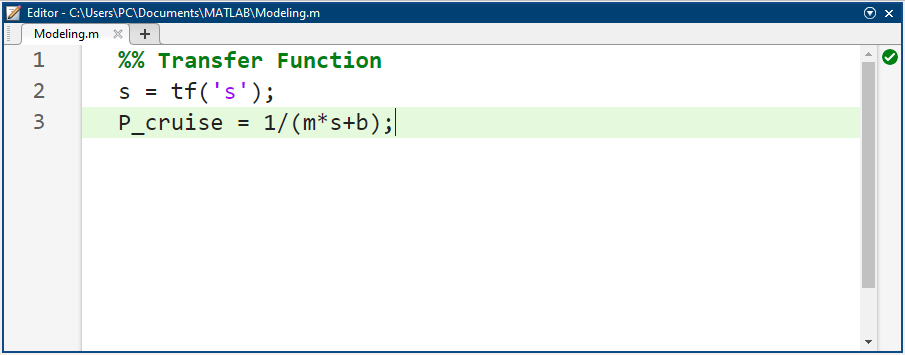
در این بخش، با استفاده از مدل فضای حالت، یک کنترلکننده و ناظر برای سیستم کروز کنترل طراحی خواهیم کرد. معادلات حرکت در قالب فضای حالت به شرح زیر هستند:
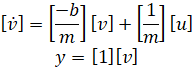
که در آن:
(m) جرم خودرو ۱۰۰۰ کیلوگرم
(b) ضریب میرایی ۵۰ نیوتن بر ثانیه بر متر
(u) نیروی کنترل اسمی ۵۰۰ نیوتن
(v) سرعت خودرو که در آن y=v خروجی سیستم است
الزامات طراحی کنترل کننده به شرح زیر است:
Rise time < 5 ثانیه
Overshoot < 10٪
Steady-state error < 2٪
طراحی کنترل با استفاده از جایگذاری قطب:
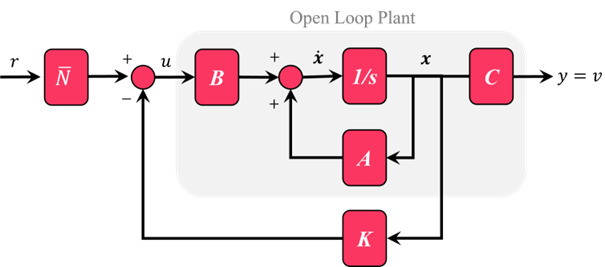
شماتیک یک سیستم فیدبک حالت کامل در شکل زیر نشان داده شده است.
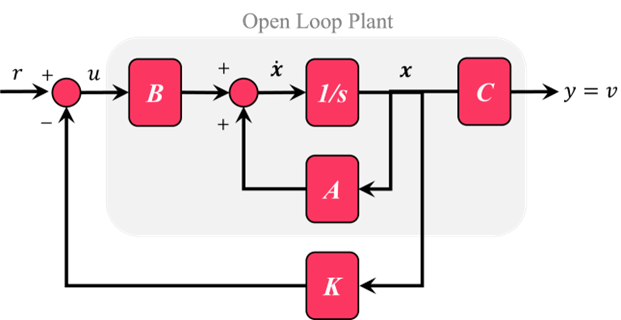
که در آن:
K = ماتریس بهره فیدبک حالت
u = r - K.x = r - K.v = ورودی کنترل
از صفحه آموزش فضای حالت به یاد بیاورید، میتوانیم از تکنیک «جایگذاری قطب» برای بدست آوردن خروجی مطلوب استفاده کنیم. قطبهای یک سیستم حلقه بسته را میتوان از معادله مشخصه پیدا کرد: دترمینان ماتریس [sI-(A-B*K)] . اگر بتوان قطبهای سیستم را با طراحی یک ماتریس کنترل (K) مناسب در مکان مورد نظر قرار داد، خروجی مطلوب را میتوان بدست آورد. در این آموزش، ابتدا قطبها انتخاب میشوند، سپس از MATLAB برای یافتن ماتریس کنترل مربوطه (K) استفاده خواهیم کرد.
حال، باید تعیین کنیم که قطبهای سیستم خود را کجا قرار دهیم. از آنجایی که ماتریس [sI-(A-B*K)] ما ۱x۱ است، فقط یک قطب برای قرار دادن داریم. فرض کنید قطب در -۱.۵ (دلخواه) باشد. درست مانند آموزش فضای حالت، از دستور place در MATLAB برای یافتن ماتریس کنترل K استفاده خواهد شد. یک m-file جدید ایجاد کنید و دستورات زیر را وارد کنید. اجرای m-file در پنجره فرمان MATLAB باید ماتریس کنترل و پاسخ پله نشان داده شده در زیر را به شما بدهد.
کد متلب:
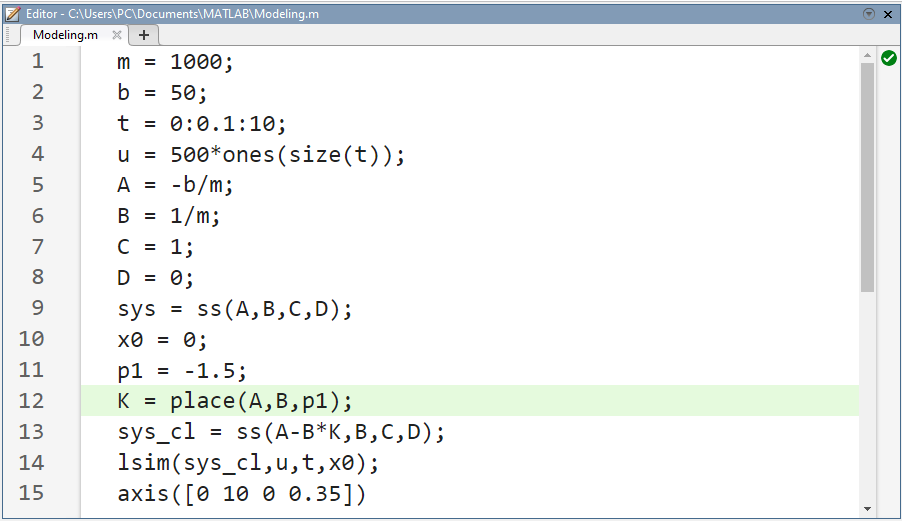
نتیجه شبیهسازی:
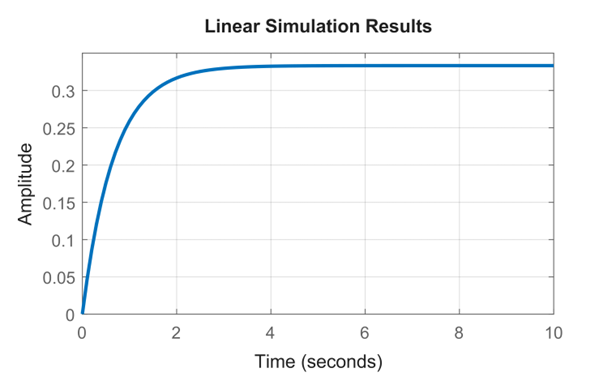
همانطور که میبینید، زمان صعود (rise time) رضایتبخش است، اما خطای حالت ماندگار خیلی زیاد است.
ورودی مرجع:
یک بار دیگر از صفحه آموزش فضای حالت، میتوان از یک ضریب مقیاسبندی به نام Nbar (شماتیک آن در زیر نشان داده شده است) برای حذف خطای حالت پایدار استفاده کرد. میتوانیم از تابع rscale برای محاسبه ضریب مقیاسبندی استفاده کنیم. ورودی از قبل در ۵۰۰ ضرب شده است و ما میخواهیم سرعت حالت پایدار ۱۰ متر بر ثانیه باشد، بنابراین باید این ضرایب را نیز در نظر بگیریم.
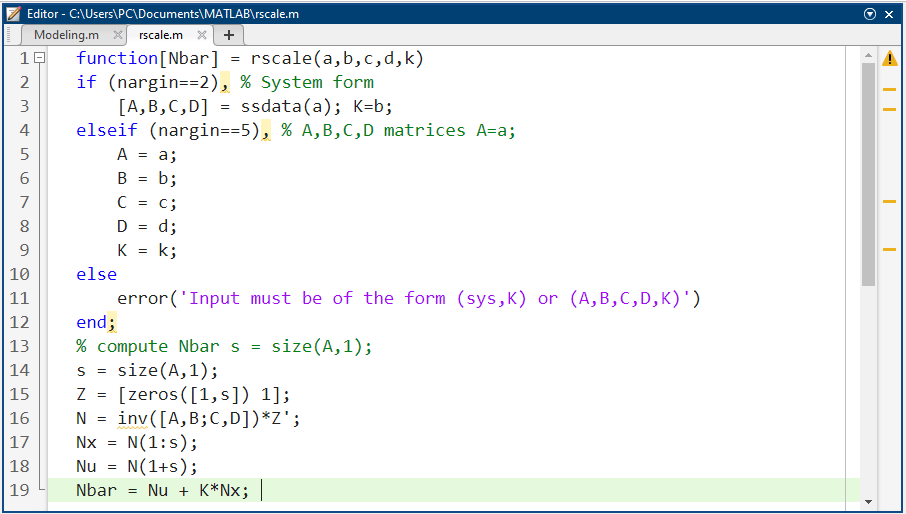
برنامه نویسی تابع rscale در متلب:
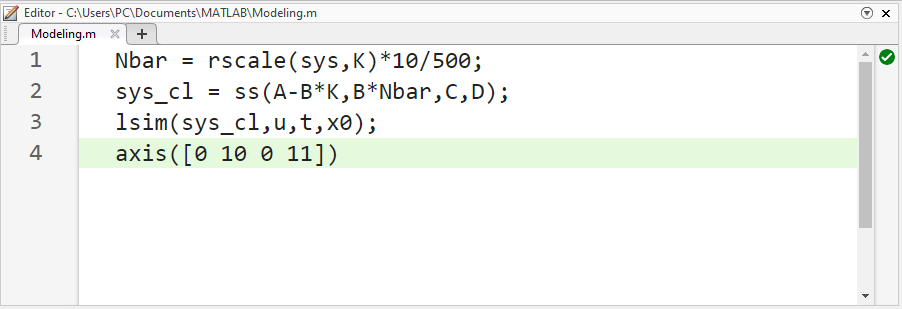
دستورات زیر را در یک m-file کپی کنید و آن را در پنجره فرمان متلب اجرا کنید. باید پاسخ مرحلهای که در زیر نشان داده شده است را دریافت کنید.
کد متلب:
نتیجه شبیهسازی:
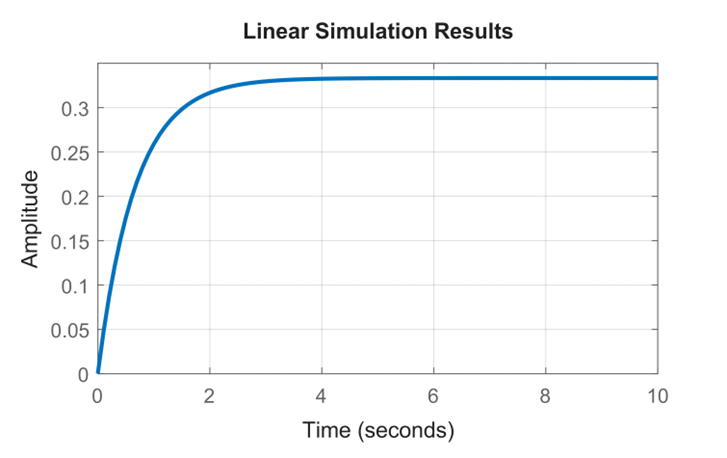
همانطور که میبینید، خطای حالت ماندگار حذف شده است. زمان خیز کمتر از ۵ ثانیه است و در واقع، فراجهش صفر است. تمام الزامات طراحی برآورده شدهاند.
منابع:
C. H. Houpis, S. N. Sheldon, and J. J. D'Azzo, Linear Control System Analysis and Design, 5th ed. Boca Raton, FL: CRC Press, 2013
Y. Bavafa-Toosi, Introduction to Linear Control Systems. Amsterdam, Netherlands: Elsevier, 2017
K. Ogata, Modern Control Engineering, 5th ed. Upper Saddle River, NJ: Pearson, 2010
N. S. Nise, Control Systems Engineering, 6th ed. Hoboken, NJ: John Wiley & Sons, 2011
C.-T. Chen, Linear System Theory and Design, 3rd ed. New York, NY: Oxford University Press, 1999
G. F. Franklin, J. D. Powell, and A. Emami-Naeini, Feedback Control of Dynamic Systems, 7th ed. Boston, MA: Pearson, 2014
#کنترل_خطی #کنترل_مدرن #کنترل_مقاوم #کنترل_فازی #کنترل_کنترل_هوشمند #کنترل_دیجیتال #کنترل_پیش_بین_مبتنی_بر_مدل #کنترل_بهینه #کنترل_چند_متغییره #کنترل_کلاسیک #کنترل_اتوماتیک #کنترل_عصبی #کنترل_چند_عاملی #کنترل_شبکهای #کنترل_تطبیقی #کنترل #کنترل_غیر_خطی #مهندسی_کنترل #متلب #سیمولینک #متلب_سیمولینک #تابع_تبدیل #معادلات_حالت #مدل_سازی #شبیهسازی #کنترل_مبتنی_بر_داده #کنترل_سیستم #سیستم #بهینه_سازی #سنسور #فیدبک #بازخورد