طراحی کنترل‌کننده فیدبک حالت برای پاندول معکوس در متلب

طراحی کنترل‌کننده فیدبک حالت برای پاندول معکوس در متلب

چکیده مطالب:

این متن به طراحی کنترل‌کننده فیدبک حالت برای یک پاندول معکوس متصل به یک ارابه موتوری در متلب می‌پردازد. هدف اصلی، حفظ تعادل پاندول در حالت عمودی رو به بالا و کنترل موقعیت ارابه است، زیرا این سیستم به طور ذاتی ناپایدار است.

فهرست مطالب

1. 1) تنظیم مسئله و الزامات طراحی
2. 2) تحلیل نیرو و معادلات سیستم
3. 3) نمایش در متلب
4. 4) پاسخ ضربه حلقه باز
5. 5) پاسخ پله حلقه باز
6. 6) قطب‌های حلقه باز
7. 7) تنظیم درجه دوم خطی (LQR)
8. 8) منابع

الزامات طراحی و تنظیم مسئله:

سیستم مورد استفاده در این مثال شامل یک پاندول معکوس است که به یک ارابه موتوری متصل شده است. سیستم پاندول معکوس نمونه‌ای است که معمولاً در کتاب‌های درسی سیستم کنترل و ادبیات تحقیقاتی یافت می‌شود. محبوبیت آن تا حدودی از این واقعیت ناشی می‌شود که بدون کنترل ناپایدار است، یعنی اگر ارابه برای حفظ تعادل حرکت داده نشود، پاندول به سادگی می‌افتد. علاوه بر این، دینامیک سیستم غیرخطی است. هدف سیستم کنترل، حفظ تعادل پاندول معکوس با اعمال نیرو به ارابه‌ای است که پاندول به آن متصل است. یک مثال واقعی که مستقیماً به این سیستم پاندول معکوس مربوط می‌شود، کنترل وضعیت یک موشک تقویت‌کننده در هنگام برخاستن است.

در این مورد، یک مسئله دوبعدی را در نظر خواهیم گرفت که در آن پاندول مقید به حرکت در صفحه عمودی نشان داده شده در شکل زیر است. برای این سیستم، ورودی کنترل، نیروی F است که ارابه را به صورت افقی حرکت می‌دهد و خروجی‌ها موقعیت زاویه‌ای تتای پاندول و موقعیت افقی ارابه x هستند.

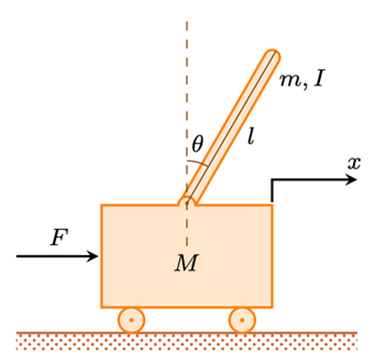
برای این مثال، مقادیر زیر را در نظر می‌گیریم:

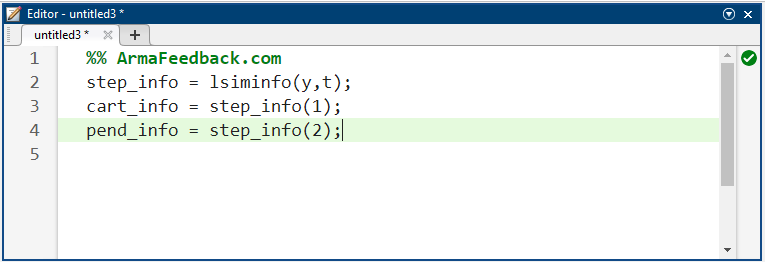
(M) جرم ارابه 0.5 کیلوگرم

(m) جرم پاندول 0.2 کیلوگرم

(b) ضریب اصطکاک ارابه 0.1 نیوتن بر متر بر ثانیه

(l) طول تا مرکز جرم پاندول 0.3 متر

(I) جرم، گشتاور اینرسی پاندول 0.006 کیلوگرم بر متر مربع

(F) نیروی اعمال شده به ارابه

(x) مختصات موقعیت ارابه

(theta) زاویه پاندول از حالت عمودی (پایین)

برای بخش‌های PID، مکان هندسی ریشه‌ها و پاسخ فرکانسی این مسئله، ما فقط به کنترل موقعیت پاندول علاقه‌مند خواهیم بود. دلیل این امر این است که تکنیک‌های مورد استفاده در این بخش‌ها برای سیستم‌های تک ورودی، تک خروجی (SISO) مناسب‌ترین هستند. بنابراین، هیچ یک از معیارهای طراحی به موقعیت ارابه نمی‌پردازند. با این حال، ما تأثیر کنترلر بر موقعیت ارابه را پس از طراحی کنترلر بررسی خواهیم کرد. برای این بخش‌ها، ما کنترلری طراحی خواهیم کرد که پاندول را پس از اینکه یک "ضربه" ضربه‌ای به ارابه وارد شد، به موقعیت عمودی رو به بالا بازگرداند. به طور خاص، معیارهای طراحی این است که پاندول ظرف 5 ثانیه به موقعیت عمودی خود بازگردد و پاندول هرگز پس از ایجاد اختلال توسط ضربه‌ای به بزرگی 1 Nsec، بیش از 0.05 رادیان از حالت عمودی دور نشود. پاندول در ابتدا در تعادل عمودی رو به بالا، تتا = پی، شروع به کار خواهد کرد.

به طور خلاصه، الزامات طراحی برای این سیستم عبارتند از:

1. 1) زمان نشست برای θ کمتر از ۵ ثانیه

2) زاویه پاندول θ هرگز نباید بیش از ۰.۰۵ رادیان از حالت عمودی باشد.

با استفاده از تکنیک‌های طراحی فضای حالت، ما به راحتی می‌توانیم یک سیستم چند خروجی را بررسی کنیم. در مورد ما، سیستم پاندول معکوس تک ورودی، چند خروجی (SIMO) است. بنابراین، برای بخش فضای حالت مثال پاندول معکوس، سعی خواهیم کرد هم زاویه پاندول و هم موقعیت ارابه را کنترل کنیم. برای چالش برانگیزتر کردن طراحی در این بخش، یک گام 0.2 متری در موقعیت مورد نظر ارابه دستور خواهیم داد. تحت این شرایط، مطلوب است که ارابه در عرض 5 ثانیه به موقعیت دستور داده شده خود برسد و زمان صعود آن کمتر از 0.5 ثانیه باشد. همچنین مطلوب است که پاندول در کمتر از 5 ثانیه به موقعیت عمودی خود برسد و علاوه بر این، زاویه پاندول بیش از 20 درجه (0.35 رادیان) از موقعیت عمودی رو به بالا تغییر نکند.

و همچنین، الزامات طراحی برای مثال فضای حالت پاندول معکوس عبارتند از:

1. 1) زمان نشست برای x و تتا کمتر از 5 ثانیه

2) زمان خیزش برای x کمتر از 0.5 ثانیه

3) زاویه تتا پاندول هرگز بیش از 20 درجه (0.35 رادیان) از حالت عمودی نباشد

4) خطای حالت پایدار کمتر از 2٪ برای x و تتا

تحلیل نیرو و معادلات سیستم:

در زیر نمودارهای جسم آزاد دو عنصر سیستم پاندول معکوس آمده است.

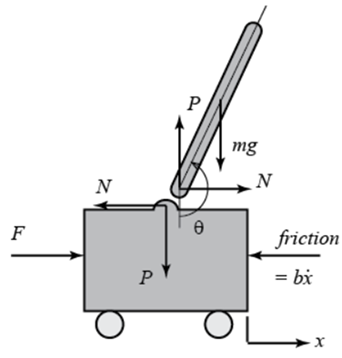
با جمع کردن نیروها در نمودار جسم آزاد ارابه در جهت افقی، معادله حرکت زیر به دست می‌آید.

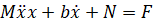
توجه داشته باشید که می‌توانید نیروهای وارد بر گاری را در جهت عمودی نیز جمع کنید، اما هیچ اطلاعات مفیدی به دست نخواهد آمد. با جمع کردن نیروها در نمودار جسم آزاد آونگ در جهت افقی، عبارت زیر برای نیروی واکنش N به دست می‌آید.

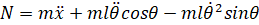
اگر این معادله را در معادله اول جایگذاری کنید، یکی از دو معادله حاکم برای این سیستم را به دست می‌آورید.

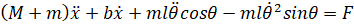
برای بدست آوردن معادله دوم حرکت برای این سیستم، نیروهای عمود بر آونگ را جمع کنید. حل سیستم در امتداد این محور، ریاضیات را بسیار ساده می‌کند. شما باید معادله زیر را بدست آورید.

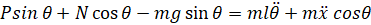
برای خلاص شدن از شر عبارات P و N در معادله بالا، گشتاورها را حول مرکز ثقل آونگ جمع کنید تا معادله زیر به دست آید.

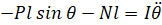
با ترکیب این دو عبارت آخر، معادله حاکم دوم به دست می‌آید.

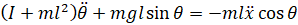
از آنجایی که تکنیک‌های تحلیل و طراحی کنترل که در این مثال به کار خواهیم برد، فقط برای سیستم‌های خطی کاربرد دارند، این مجموعه معادلات باید خطی شوند. به طور خاص، ما معادلات مربوط به موقعیت تعادل عمودی رو به بالا، تتا = پی، را خطی خواهیم کرد و فرض خواهیم کرد که سیستم در یک همسایگی کوچک از این تعادل باقی می‌ماند. این فرض باید به طور منطقی معتبر باشد زیرا تحت کنترل، می‌خواهیم که پاندول بیش از 20 درجه از موقعیت عمودی رو به بالا منحرف نشود. فرض کنید فی نشان‌دهنده انحراف موقعیت پدال از تعادل باشد، یعنی تتا = پی + فی. دوباره با فرض انحراف کوچک (فی) از تعادل، می‌توانیم از تقریب‌های زاویه کوچک زیر از توابع غیرخطی در معادلات سیستم خود استفاده کنیم:

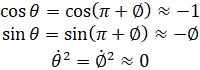
پس از جایگذاری تقریب‌های فوق در معادلات حاکم غیرخطی، به دو معادله خطی‌شده حرکت می‌رسیم. توجه داشته باشید که u جایگزین ورودی F شده است.

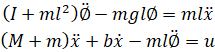
تابع تبدیل:

برای بدست آوردن توابع تبدیل معادلات سیستم خطی شده، ابتدا باید تبدیل لاپلاس معادلات سیستم را با فرض شرایط اولیه صفر بدست آوریم. تبدیل‌های لاپلاس حاصل در زیر نشان داده شده‌اند.

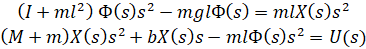
به یاد داشته باشید که یک تابع تبدیل، رابطه بین یک ورودی و یک خروجی را در یک زمان نشان می‌دهد. برای یافتن اولین تابع تبدیل برای خروجی Phi(s) و ورودی U(s)، باید X(s) را از معادلات بالا حذف کنیم. معادله اول را برای X(s) حل کنید.

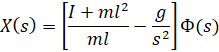
سپس موارد فوق را در معادله دوم جایگزین کنید.       

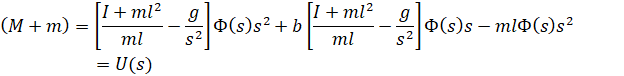
با مرتب‌سازی مجدد، تابع تبدیل به صورت زیر خواهد بود:

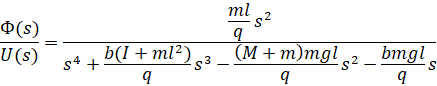
که،

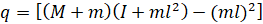
از تابع تبدیل بالا می‌توان دریافت که در مبدا هم قطب و هم صفر وجود دارد. این دو را می‌توان حذف کرد و تابع تبدیل به صورت زیر می‌شود.

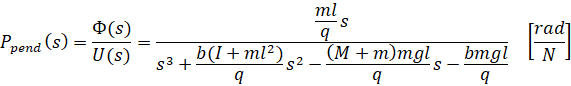
دوم، تابع تبدیل با موقعیت سبد X(s) به عنوان خروجی را می‌توان به روشی مشابه استخراج کرد تا به رابطه زیر برسیم.

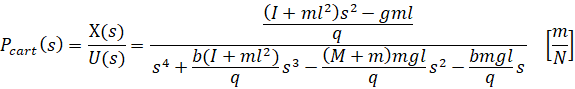
فضای حالت

معادلات خطی‌شده حرکت از بالا را می‌توان در قالب فضای حالت نیز نمایش داد، اگر آنها را به صورت مجموعه‌ای از معادلات دیفرانسیل مرتبه اول بازآرایی کنیم. از آنجایی که معادلات خطی هستند، می‌توان آنها را به شکل ماتریسی استاندارد نشان داده شده در زیر قرار داد:

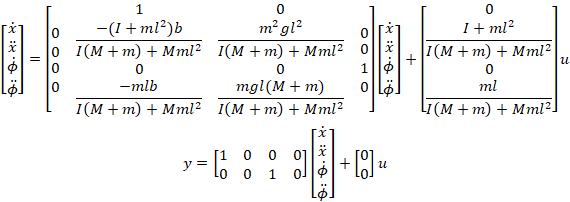
ماتریس C دارای دو سطر است زیرا هم موقعیت گاری و هم موقعیت پاندول بخشی از خروجی هستند. به طور خاص، موقعیت گاری اولین عنصر خروجی y و انحراف پاندول از موقعیت تعادلش دومین عنصر y است.

نمایش در متلب:

1. تابع تبدیل

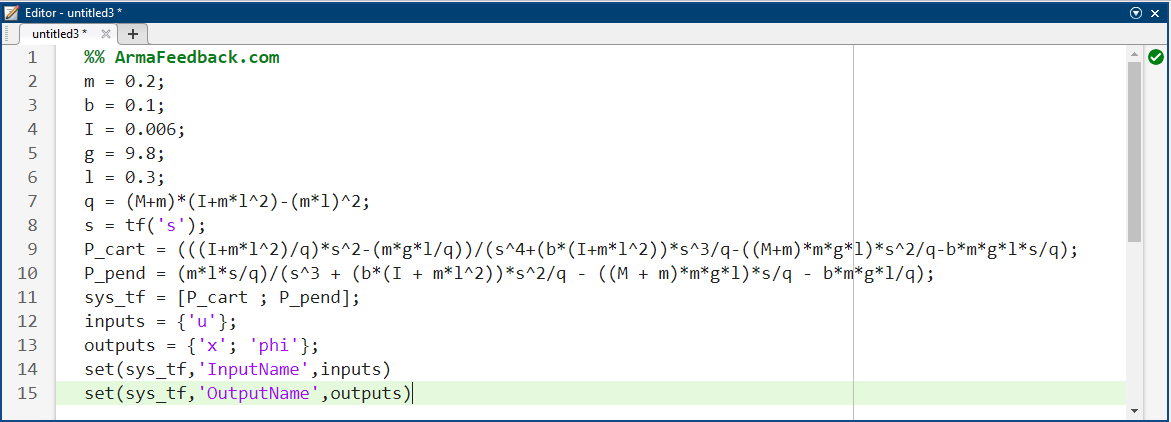
می‌توانیم توابع انتقال مشتق شده در بالا را برای سیستم پاندول معکوس در متلب با استفاده از دستورات زیر نمایش دهیم. توجه داشته باشید که می‌توانید به خروجی‌ها (و ورودی‌ها) نام بدهید تا بین موقعیت ارابه و موقعیت پاندول تمایز قائل شوید. اجرای این کد در پنجره فرمان، خروجی نشان داده شده در زیر را تولید می‌کند.

کد متلب:

فضای حالت

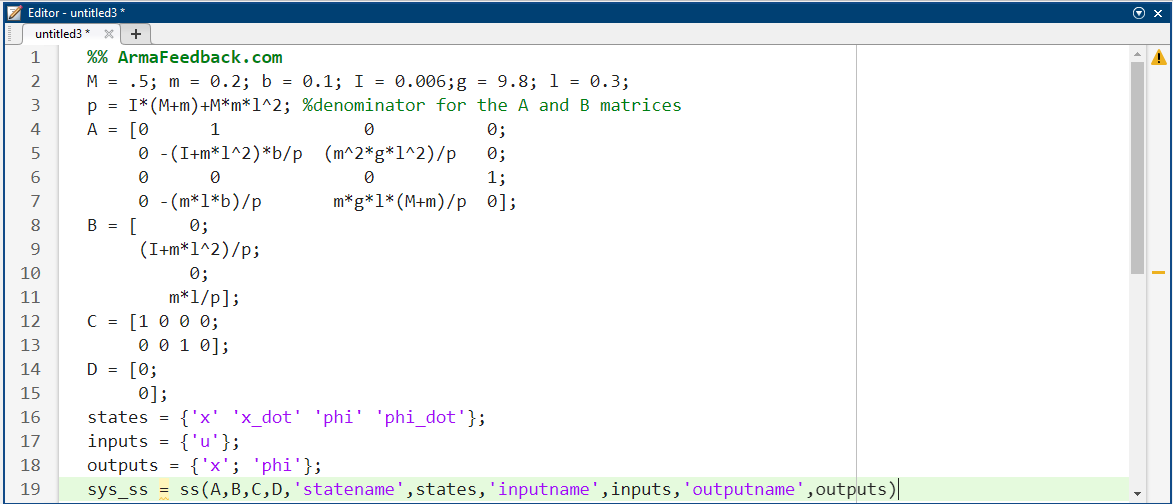
همچنین می‌توانیم سیستم را با استفاده از معادلات فضای حالت نمایش دهیم. دستورات اضافی متلب که در ادامه آمده‌اند، یک مدل فضای حالت از پاندول معکوس ایجاد می‌کنند و خروجی نشان داده شده در زیر را هنگام اجرا در پنجره فرمان متلب تولید می‌کنند. مجدداً توجه داشته باشید که نام ورودی‌ها، خروجی‌ها و حالت‌ها را می‌توان مشخص کرد تا درک مدل آسان‌تر شود.

کدمتلب:

مدل فضای حالت فوق را می‌توان با استفاده از دستور tf مطابق شکل زیر به فرم تابع تبدیل نیز تبدیل کرد. برعکس، مدل تابع تبدیل را می‌توان با استفاده از دستور ss به فرم فضای حالت تبدیل کرد.

کد متلب:

با بررسی موارد فوق، به وجود برخی از عبارات با ضرایب بسیار کوچک توجه کنید. این عبارات در واقع باید صفر باشند و به دلیل خطاهای گرد کردن عددی که در الگوریتم‌های تبدیل متلب جمع می‌شوند، ظاهر می‌شوند. اگر این ضرایب را روی صفر تنظیم کنید، مدل‌های تابع انتقال فوق با مدل‌هایی که قبلاً در بخش تابع انتقال مثال تولید شده‌اند، مطابقت خواهند داشت.

تحلیل سیستم پاندول معکوس

از مسئله اصلی، توابع تبدیل حلقه باز سیستم پاندول معکوس را به صورت زیر استخراج کردیم.

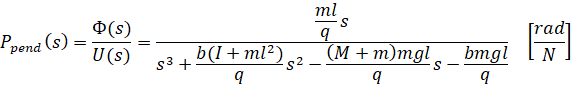
و

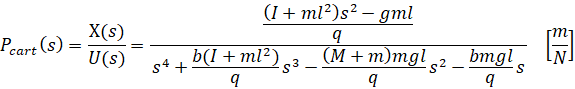
که

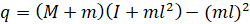
به یاد بیاورید که دو تابع انتقال فوق فقط برای مقادیر کوچک زاویه فی، که جابجایی زاویه‌ای آونگ از موقعیت عمودی به سمت بالا است، معتبر هستند. همچنین، زاویه مطلق آونگ تتا برابر با پی + فی است.

با توجه به پاسخ پاندول به ضربه ۱ نیوتن ثانیه‌ای اعمال شده به ارابه، الزامات طراحی برای پاندول عبارتند از:

زمان نشست برای تتا کمتر از ۵ ثانیه

زاویه تتا پاندول هرگز بیش از ۰.۰۵ رادیان از حالت عمودی نباشد

علاوه بر این، الزامات پاسخ سیستم به فرمان گام ۰.۲ متری در موقعیت ارابه عبارتند از:

زمان نشست برای x و تتا کمتر از ۵ ثانیه

زمان خیزش برای x کمتر از ۰.۵ ثانیه

زاویه تتا پاندول هرگز بیش از ۲۰ درجه (۰.۳۵ رادیان) از حالت عمودی نباشد

پاسخ ضربه حلقه باز

ما با بررسی پاسخ حلقه باز سیستم پاندول معکوس شروع خواهیم کرد. یک m-file جدید ایجاد کنید و دستورات زیر را برای ایجاد مدل سیستم تایپ کنید (برای جزئیات دریافت این دستورات به مسئله اصلی مراجعه کنید).

کد متلب:

اکنون می‌توانیم پاسخ ضربه حلقه باز سیستم را بررسی کنیم. به طور خاص، با استفاده از دستور ضربه متلب، نحوه پاسخ سیستم به نیروی ضربه‌ای اعمال شده به گاری را بررسی خواهیم کرد. دستورات زیر را به انتهای m-file اضافه کنید و آن را در پنجره فرمان متلب اجرا کنید تا نمودار مربوطه که در زیر نشان داده شده است را بدست آورید.

کد متلب:

نتایج شبیه‌سازی:

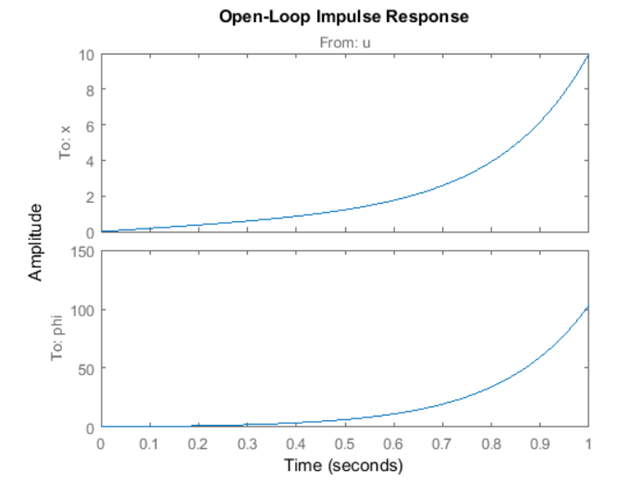
همانطور که از نمودار می‌بینید، پاسخ سیستم کاملاً رضایت‌بخش نیست. در واقع، در حلقه باز پایدار نیست. اگرچه نشان داده شده است که موقعیت پاندول پس از ۱۰۰ رادیان (۱۵ دور) افزایش می‌یابد، اما این مدل فقط برای فی‌های کوچک معتبر است. همچنین می‌توانید ببینید که موقعیت گاری بی‌نهایت به سمت راست حرکت می‌کند، اگرچه هیچ الزامی برای موقعیت گاری برای ورودی نیروی ضربه‌ای وجود ندارد.

قطب‌های یک سیستم همچنین می‌توانند در مورد پاسخ زمانی آن به ما اطلاعات بدهند. از آنجایی که سیستم ما دو خروجی و یک ورودی دارد، توسط دو تابع انتقال توصیف می‌شود. به طور کلی، تمام توابع انتقال از هر ورودی به هر خروجی یک سیستم چند ورودی، چند خروجی (MIMO) قطب‌های یکسانی (اما صفرهای متفاوت) خواهند داشت، مگر اینکه حذف قطب-صفر وجود داشته باشد. ما به طور خاص قطب‌ها و صفرهای سیستم را با استفاده از تابع zpkdata در متلب بررسی خواهیم کرد. پارامتر 'v' که در زیر نشان داده شده است، قطب‌ها و صفرها را به عنوان بردارهای ستونی به جای آرایه‌های سلولی برمی‌گرداند.

صفرها و قطب‌های سیستمی که در آن موقعیت آونگ خروجی است، به صورت زیر یافت می‌شوند:

کد متلب:

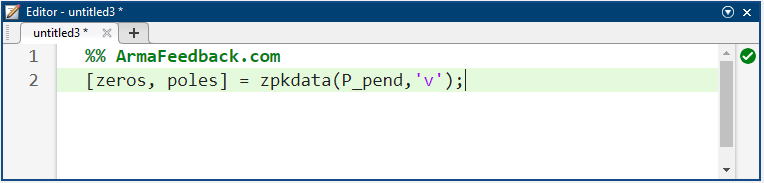
به همین ترتیب، صفرها و قطب‌های سیستمی که در آن موقعیت چرخ دستی خروجی است، به صورت زیر یافت می‌شوند:

کد متلب:

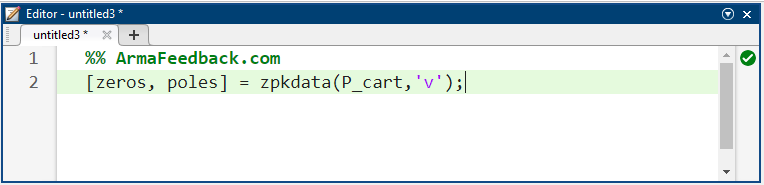
همانطور که پیش‌بینی می‌شد، قطب‌های هر دو تابع تبدیل یکسان هستند. قطب واقع در ۵.۵۶۵۱ نشان می‌دهد که سیستم ناپایدار است زیرا قطب دارای بخش حقیقی مثبت است. به عبارت دیگر، قطب در نیمه سمت راست صفحه s مختلط قرار دارد. این با آنچه در بالا مشاهده کردیم مطابقت دارد.

پاسخ پله حلقه باز

از آنجایی که سیستم دارای قطبی با بخش حقیقی مثبت است، پاسخ آن به ورودی پله نیز به صورت نامحدود رشد خواهد کرد. ما این موضوع را با استفاده از دستور lsim که می‌تواند برای شبیه‌سازی پاسخ مدل‌های LTI به ورودی‌های دلخواه استفاده شود، تأیید خواهیم کرد. در این حالت، از ورودی پله ۱ نیوتنی استفاده خواهد شد. اضافه کردن کد زیر به m-file و اجرای آن در پنجره فرمان متلب، نمودار نشان داده شده در زیر را ایجاد می‌کند.

کد متلب:

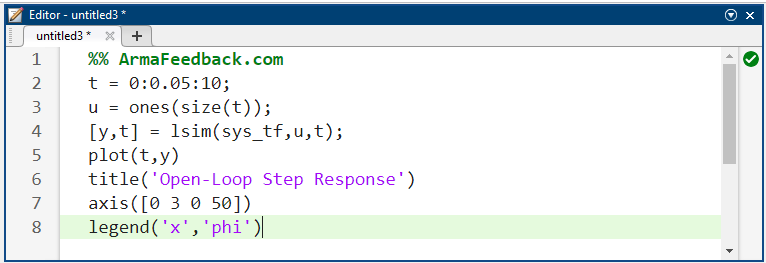
نتیجه شبیه‌سازی:

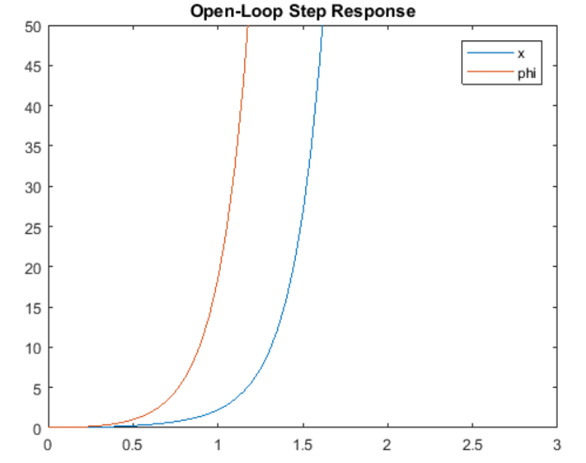
کد متلب:

نتایج فوق انتظار ما را مبنی بر ناپایدار بودن پاسخ سیستم به ورودی پله تأیید می‌کند. از تحلیل بالا مشخص است که برای بهبود پاسخ سیستم، باید نوعی کنترل طراحی شود.

نکته: راه‌حل‌های نشان داده شده در مثال‌های PID، مکان هندسی ریشه‌ها و پاسخ فرکانسی ممکن است یک کنترل‌کننده کارآمد برای مسئله پاندول معکوس ارائه ندهند. همانطور که قبلاً گفته شد، وقتی پاندول معکوس را به عنوان یک سیستم تک ورودی، تک خروجی در نظر می‌گیریم، موقعیت ارابه، x، را نادیده می‌گیریم. در صورت امکان در این مثال‌ها، نشان خواهیم داد که وقتی یک کنترل‌کننده روی سیستم پیاده‌سازی می‌شود، چه اتفاقی برای موقعیت ارابه می‌افتد.

روش‌های فضای حالت برای طراحی کنترل‌کننده

از مسئله اصلی، معادلات دینامیکی سیستم پاندول معکوس در فرم فضای حالت به شرح زیر است:

برای مشاهده‌ی چگونگی طرح اولیه‌ی این مسئله و استخراج معادلات سیستم، به صفحه‌ی پاندول معکوس: مدل‌سازی سیستم مراجعه کنید. خروجی‌های این مسئله، جابجایی ارابه (x بر حسب متر) و زاویه‌ی پاندول (π بر حسب رادیان) هستند که در آن π نشان‌دهنده‌ی انحراف موقعیت پدال از حالت تعادل است، یعنی تتا = π + π.

معیارهای طراحی این سیستم برای یک پله 0.2 متری در موقعیت دلخواه ارابه x به شرح زیر است:

زمان نشست برای x و تتا کمتر از 5 ثانیه

زمان خیز برای x کمتر از 0.5 ثانیه

زاویه پاندول تتا هرگز بیش از 20 درجه (0.35 رادیان) از حالت عمودی نباشد

خطای حالت پایدار کمتر از 2٪ برای x و تتا

همانطور که اگر برخی از مثال‌های دیگر پاندول معکوس را مرور کرده باشید، ممکن است متوجه شده باشید، معیارهای طراحی برای این مثال متفاوت است. در مثال‌های دیگر، ما تلاش می‌کردیم پاندول را در پاسخ به نیروی اغتشاش ضربه‌ای اعمال شده به گاری، عمودی نگه داریم. ما تلاشی برای کنترل موقعیت گاری نکردیم. در این مثال، ما تلاش می‌کنیم پاندول را عمودی نگه داریم در حالی که موقعیت گاری را برای حرکت ۰.۲ متر به سمت راست کنترل می‌کنیم. رویکرد طراحی فضای حالت برای کنترل چندین خروجی، همانطور که در اینجا داریم، بسیار مناسب است.

این مشکل را می‌توان با استفاده از فیدبک حالت کامل حل کرد. شماتیک این نوع سیستم کنترل در زیر نشان داده شده است که در آن K ماتریسی از بهره‌های کنترل است. توجه داشته باشید که در اینجا ما به جای استفاده از خروجی‌های سیستم برای فیدبک، تمام حالت‌های سیستم را فیدبک می‌کنیم.

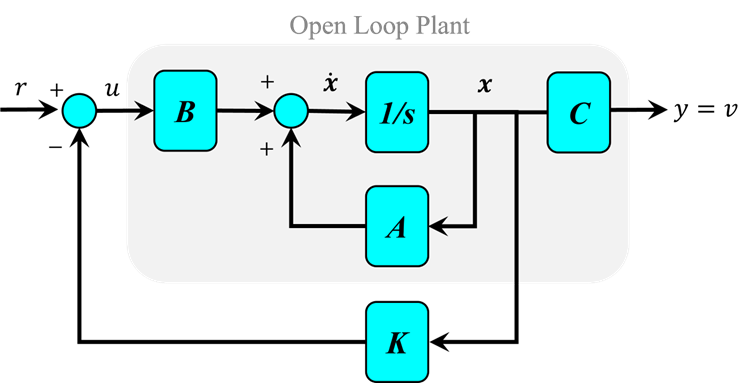
قطب‌های حلقه باز

در این مسئله، r نشان دهنده فرمان پله موقعیت گاری است. 4 حالت نشان دهنده موقعیت و سرعت گاری و زاویه و سرعت زاویه‌ای پاندول هستند. خروجی y شامل موقعیت گاری و زاویه پاندول است. ما می‌خواهیم کنترل‌کننده‌ای طراحی کنیم که وقتی یک مرجع پله به سیستم داده می‌شود، پاندول باید جابجا شود، اما در نهایت به صفر (یعنی عمودی) برگردد و گاری باید به موقعیت فرمان داده شده جدید خود حرکت کند. برای مشاهده پاسخ حلقه باز سیستم، لطفاً به صفحه پاندول معکوس: تحلیل سیستم مراجعه کنید.

اولین قدم در طراحی یک کنترل‌کننده فیدبک حالت کامل، تعیین قطب‌های حلقه باز سیستم است. خطوط کد زیر را در یک m-file وارد کنید. پس از اجرا در پنجره فرمان متلب، خروجی، قطب‌های حلقه باز (مقادیر ویژه A) را مطابق شکل زیر فهرست می‌کند.

کد متلب:

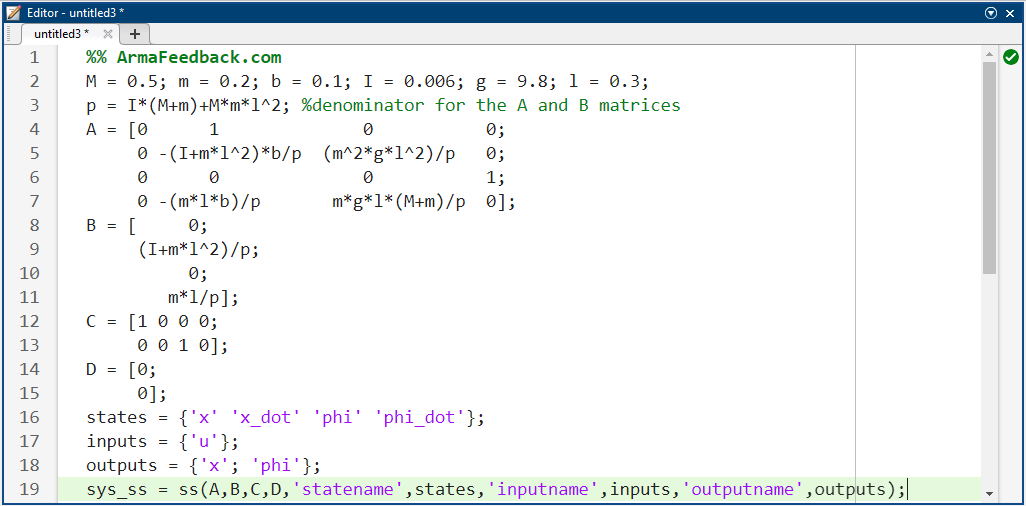
همانطور که می‌بینید، یک قطب صفحه راست در ۵.۵۶۵۱ وجود دارد. این باید حدس شما را مبنی بر ناپایدار بودن سیستم در حالت حلقه باز تأیید کند.

تنظیم خطی درجه دوم (LQR) یا فیدبک حالت بهینه:

گام بعدی در فرآیند طراحی، یافتن بردار بهره‌های کنترل فیدبک حالت K است، با فرض اینکه به هر چهار متغیر حالت دسترسی داریم (یعنی می‌توانیم اندازه‌گیری کنیم). این کار را می‌توان به روش‌های مختلفی انجام داد. اگر مکان قطب‌های حلقه بسته مورد نظر را می‌دانید، می‌توانید از دستورات place یا acker در متلب استفاده کنید. گزینه دیگر استفاده از دستور lqr است که بهره بهینه کنترل‌کننده را با فرض یک سیستم خطی، تابع هزینه درجه دوم و مرجع برابر با صفر برمی‌گرداند (برای جزئیات بیشتر به کتاب درسی خود مراجعه کنید).

قبل از طراحی کنترل‌کننده، ابتدا بررسی می‌کنیم که سیستم قابل کنترل است. برآورده شدن این ویژگی به این معنی است که می‌توانیم حالت سیستم را در هر زمان محدود (تحت محدودیت‌های فیزیکی سیستم) به هر جایی که دوست داریم هدایت کنیم. برای اینکه سیستم کاملاً قابل کنترل باشد، ماتریس کنترل‌پذیری باید رتبه n داشته باشد که در آن رتبه یک ماتریس، تعداد سطرها (یا ستون‌های) مستقل خطی است. ماتریس کنترل‌پذیری سیستم به شکل زیر نشان داده می‌شود. عدد n مربوط به تعداد متغیرهای حالت سیستم است. اضافه کردن عبارات اضافی به ماتریس کنترل‌پذیری با توان‌های بالاتر ماتریس A، رتبه ماتریس کنترل‌پذیری را افزایش نمی‌دهد، زیرا این عبارات اضافی فقط ترکیب‌های خطی از عبارات قبلی خواهند بود.

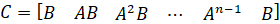
از آنجایی که ماتریس کنترل‌پذیری ما ۴x۴ است، رتبه ماتریس باید ۴ باشد. ما از دستور ctrb در متلب برای تولید ماتریس کنترل‌پذیری و از دستور rank در متلب برای آزمایش رتبه ماتریس استفاده خواهیم کرد. اضافه کردن دستورات اضافی زیر به m-file و اجرا در پنجره فرمان متلب، خروجی زیر را تولید خواهد کرد.

کد متلب:

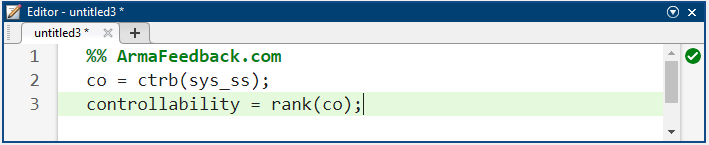
بنابراین، ما تأیید کرده‌ایم که سیستم ما قابل کنترل است و بنابراین باید بتوانیم کنترل‌کننده‌ای را طراحی کنیم که الزامات داده شده را برآورده کند. به طور خاص، ما از روش تنظیم درجه دوم خطی برای تعیین ماتریس بهره کنترل فیدبک حالت K خود استفاده خواهیم کرد. تابع lqr متلب به شما امکان می‌دهد دو پارامتر R و Q را انتخاب کنید که اهمیت نسبی تلاش کنترلی (u) و خطا (انحراف از 0) را به ترتیب در تابع هزینه‌ای که سعی در بهینه‌سازی آن دارید، متعادل می‌کنند. ساده‌ترین حالت این است که فرض کنید R=1 و Q = C' C باشد. تابع هزینه مربوط به این R و Q اهمیت یکسانی را برای متغیرهای کنترل و حالت که خروجی هستند (زاویه پاندول و موقعیت ارابه) قائل می‌شود. اساساً، روش lqr امکان کنترل هر دو خروجی را فراهم می‌کند. در این حالت، انجام این کار بسیار آسان است. کنترل‌کننده را می‌توان با تغییر عناصر غیر صفر در ماتریس Q تنظیم کرد تا به پاسخ مطلوب دست یافت. برای مشاهده ساختار Q، موارد زیر را در پنجره فرمان متلب وارد کنید تا خروجی داده شده در زیر را ببینید.

کد متلب:

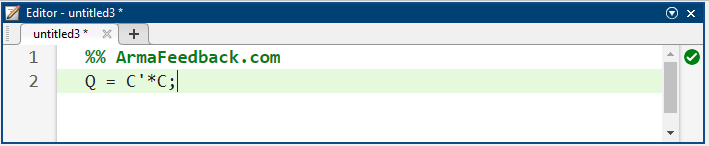
عنصر در موقعیت (1،1) از Q نشان دهنده وزن روی موقعیت گاری و عنصر در موقعیت (3،3) نشان دهنده وزن روی زاویه پاندول است. وزن ورودی R در 1 باقی خواهد ماند. در نهایت آنچه مهم است مقدار نسبی Q و R است، نه مقادیر مطلق آنها. اکنون که می‌دانیم چگونه ماتریس Q را تفسیر کنیم، می‌توانیم آزمایش کنیم تا ماتریس K را پیدا کنیم که یک کنترل‌کننده "خوب" به ما می‌دهد. ما ادامه می‌دهیم و ماتریس K را پیدا می‌کنیم و پاسخ را در یک مرحله رسم می‌کنیم تا تغییرات در کنترل ایجاد شود و به طور خودکار در پاسخ مشاهده شود. دستورات زیر را به انتهای فایل m خود اضافه کنید و در پنجره فرمان متلب اجرا کنید تا مقدار زیر برای K و نمودار پاسخ نشان داده شده در زیر را بدست آورید.

کد متلب:

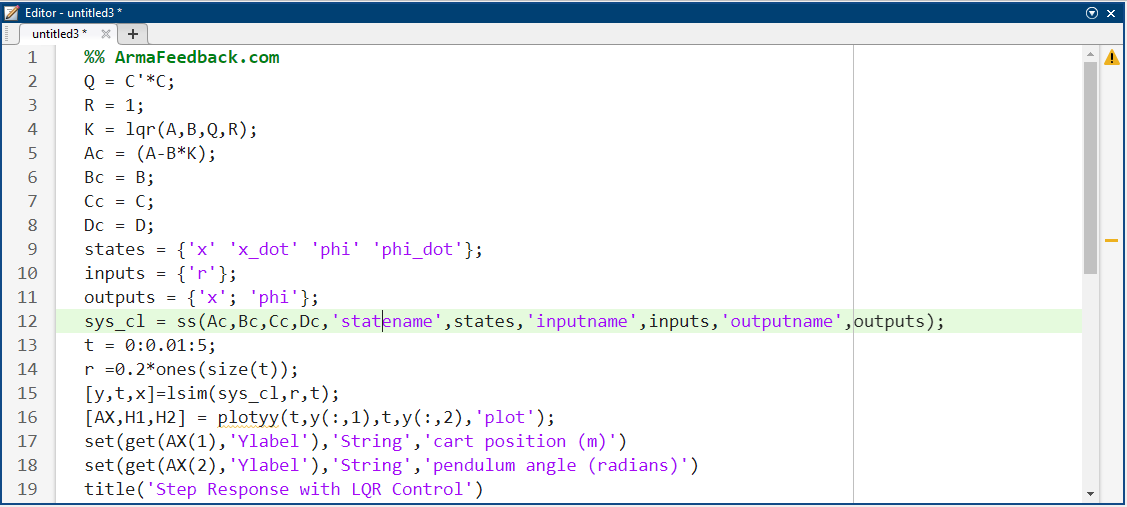
نتیجه شبیه‌سازی:

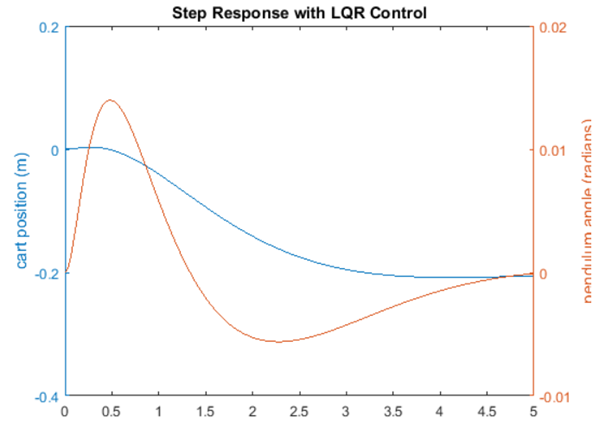
منحنی قرمز نشان دهنده زاویه پاندول بر حسب رادیان و منحنی آبی نشان دهنده موقعیت ارابه بر حسب متر است. همانطور که می‌بینید، این نمودار رضایت‌بخش نیست. جهش پاندول و ارابه خوب به نظر می‌رسد، اما زمان‌های نشست آنها نیاز به بهبود دارد و زمان خیزش ارابه باید کاهش یابد. همانطور که مطمئنم متوجه شده‌اید، موقعیت نهایی ارابه نیز نزدیک به محل مورد نظر نیست، بلکه در واقع در جهت مخالف حرکت کرده است. این خطا در بخش بعدی بررسی خواهد شد و در حال حاضر ما بر زمان‌های نشست و خیزش تمرکز خواهیم کرد. به فایل m خود برگردید و ماتریس Q را تغییر دهید تا ببینید آیا می‌توانید پاسخ بهتری دریافت کنید یا خیر. متوجه خواهید شد که افزایش عناصر (1،1) و (3،3) باعث کاهش زمان‌های نشست و خیزش و کاهش زاویه حرکت پاندول می‌شود. به عبارت دیگر، شما وزن بیشتری را به خطاها تحمیل می‌کنید، به قیمت افزایش تلاش کنترلی u. با تغییر m-file خود به طوری که عنصر (1,1) از Q برابر با 5000 و عنصر (3,3) برابر با 100 باشد، مقدار K زیر و پاسخ پله نشان داده شده در زیر تولید خواهد شد.

کد متلب:

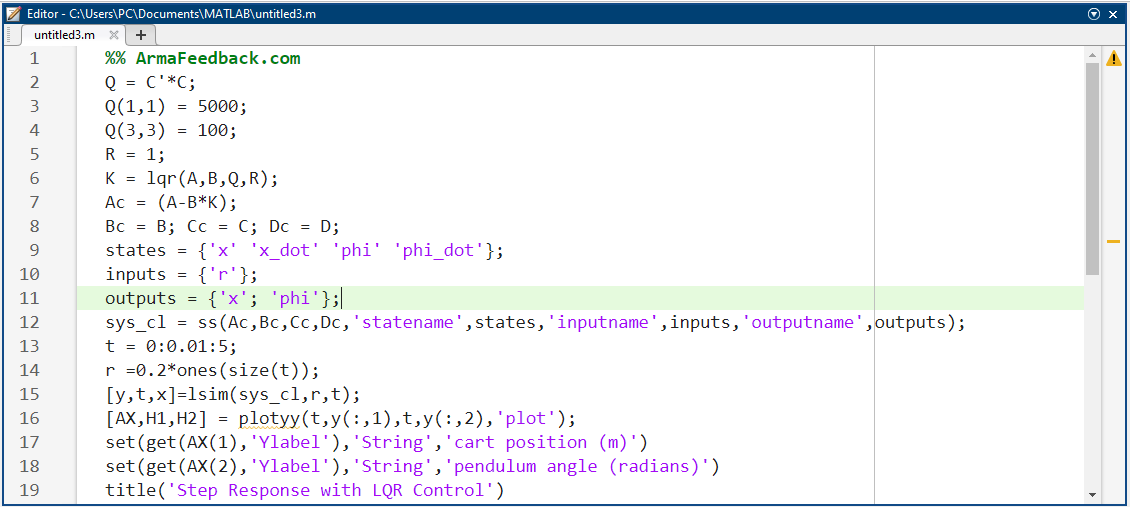
نتیجه شبیه‌سازی:

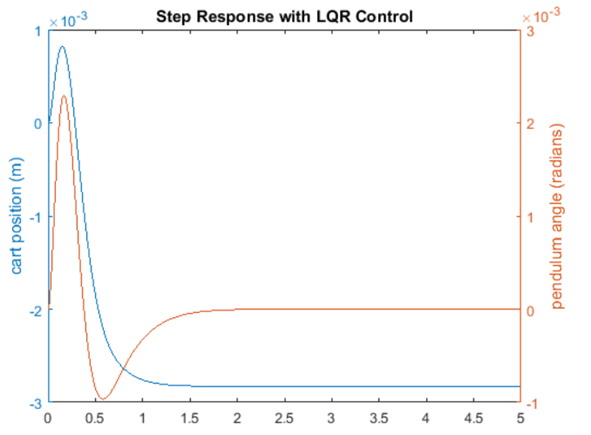
شاید متوجه شده باشید که اگر مقادیر عناصر Q را حتی بیشتر افزایش دهید، می‌توانید پاسخ را حتی بیشتر بهبود بخشید. دلیل انتخاب این وزن‌دهی این بود که الزامات طراحی گذرا را برآورده می‌کند. افزایش بیشتر مقدار Q باعث می‌شود خطای ردیابی کوچکتر شود، اما به نیروی کنترلی u بیشتری نیاز دارد. تلاش کنترلی بیشتر معمولاً با هزینه بیشتر (انرژی بیشتر، محرک بزرگتر و غیره) مطابقت دارد.

منابع:

C. H. Houpis, S. N. Sheldon, and J. J. D'Azzo, Linear Control System Analysis and Design, 5th ed. Boca Raton, FL: CRC Press, 2013

Y. Bavafa-Toosi, Introduction to Linear Control Systems. Amsterdam, Netherlands: Elsevier, 2017

K. Ogata, Modern Control Engineering, 5th ed. Upper Saddle River, NJ: Pearson, 2010

N. S. Nise, Control Systems Engineering, 6th ed. Hoboken, NJ: John Wiley & Sons, 2011

C.-T. Chen, Linear System Theory and Design, 3rd ed. New York, NY: Oxford University Press, 1999

G. F. Franklin, J. D. Powell, and A. Emami-Naeini, Feedback Control of Dynamic Systems, 7th ed. Boston, MA: Pearson, 2014

#کنترل_خطی #کنترل_مدرن #کنترل_مقاوم #کنترل_فازی #کنترل_کنترل_هوشمند #کنترل_دیجیتال #کنترل_پیش_بین_مبتنی_بر_مدل #کنترل_بهینه #کنترل_چند_متغییره #کنترل_کلاسیک #کنترل_اتوماتیک #کنترل_عصبی #کنترل_چند_عاملی #کنترل_شبکه‌ای #کنترل_تطبیقی #کنترل #کنترل_غیر_خطی #مهندسی_کنترل #متلب #سیمولینک#متلب_سیمولینک #تابع_تبدیل #معادلات_حالت #مدل_سازی #شبیه‌سازی #کنترل_مبتنی_بر_داده #کنترل_سیستم #سیستم #بهینه_سازی #سنسور #فیدبک #بازخورد#پاندول_معکوس

آکادمی آرمـــا فیدبــک