مدل سازی و طراحی کنترلر برای سیستم توپ معلق مغناطیسی در متلب

مدل سازی و طراحی کنترلر برای سیستم توپ معلق مغناطیسی در متلب

فهرست مطالب

1. مدل‌سازی
2. پایداری
3. کنترل‌پذیری و رویت‌پذیری
4. طراحی کنترل با استفاده از جایگذاری قطب
5. معرفی ورودی مرجع
6. طراحی رویتگر
7. منابع

در این بخش، نحوه طراحی کنترل‌کننده‌ها و رویتگرها را با استفاده از روش‌های فضای حالت (یا حوزه زمان) نشان خواهیم داد.

1. مدل‌سازی

    

روش‌های مختلفی برای توصیف یک سیستم معادلات دیفرانسیل خطی وجود دارد. نمایش فضای حالت در بخش مقدمه، مدل‌سازی سیستم معرفی شد. برای یک سیستم خطی تغییرناپذیر با زمان SISO LTI، فرم فضای حالت در زیر آورده شده است:

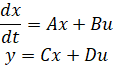
که در آن x یک بردار n در ۱ است که متغیرهای حالت سیستم را نشان می‌دهد، u یک اسکالر است که ورودی را نشان می‌دهد و y یک اسکالر است که خروجی را نشان می‌دهد. ماتریس‌های A (n در n)، B (n در ۱) و C (1 در n) روابط بین متغیرهای حالت و ورودی و خروجی را تعیین می‌کنند. توجه داشته باشید که n معادله دیفرانسیل مرتبه اول وجود دارد. نمایش فضای حالت همچنین می‌تواند برای سیستم‌هایی با چندین ورودی و چندین خروجی (MIMO) استفاده شود، اما ما در این آموزش‌ها عمدتاً بر سیستم‌های تک ورودی، تک خروجی (SISO) تمرکز خواهیم کرد.

برای معرفی روش طراحی کنترل فضای حالت، از توپ معلق مغناطیسی به عنوان مثال استفاده خواهیم کرد. جریان عبوری از سیم‌پیچ‌ها، نیروی مغناطیسی القا می‌کند که می‌تواند نیروی جاذبه را متعادل کند و باعث شود توپ (که از ماده مغناطیسی ساخته شده است) در هوا معلق بماند. مدل‌سازی این سیستم در بسیاری از کتاب‌های درسی کنترل (از جمله سیستم‌های کنترل اتوماتیک، ویرایش هفتم) ارائه شده است.

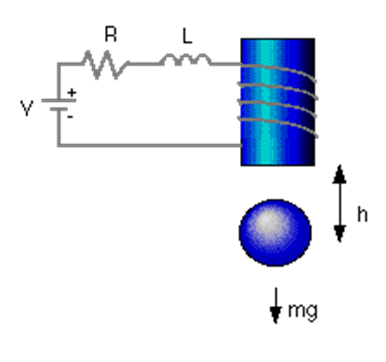
عادلات مربوط به سیستم به صورت زیر ارائه می‌شوند:

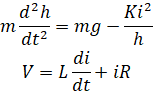
که در آن h موقعیت عمودی توپ، i جریان عبوری از آهنربای الکتریکی، V ولتاژ اعمالی، m جرم توپ، g شتاب ناشی از گرانش، L اندوکتانس، R مقاومت و K ضریبی است که نیروی مغناطیسی وارد بر توپ را تعیین می‌کند. برای سادگی، مقادیر m = 0.05 kg، K = 0.0001، L = 0.01 H، R = 1 Ohm، g = 9.81 m/s^2 را انتخاب می‌کنیم. سیستم در حالت تعادل است (توپ در هوا معلق است) هر زمان که h = K i^2/mg باشد (که در آن نقطه dh/dt = 0 است). معادلات را در مورد نقطه h = 0.01 m (جایی که جریان اسمی حدود 7 آمپر است) خطی می‌کنیم و معادلات فضای حالت خطی را بدست می‌آوریم:

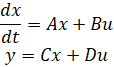
که

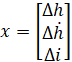
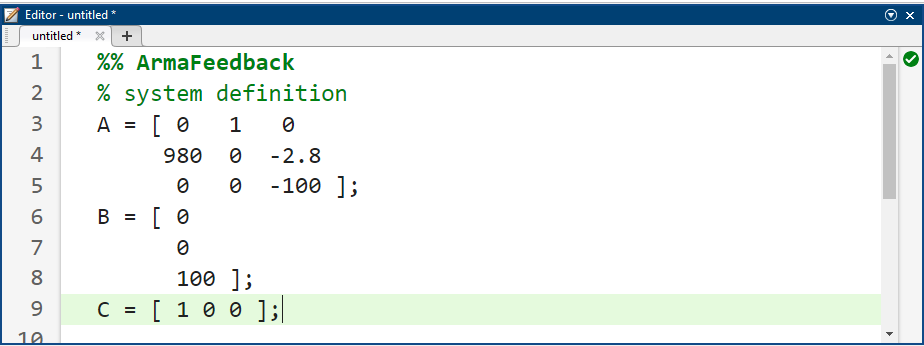
مجموعه متغیرهای حالت برای سیستم (یک بردار ۳x۱)، u انحراف ولتاژ ورودی از مقدار تعادل آن (دلتا V) و y (خروجی) انحراف ارتفاع توپ از موقعیت تعادل آن (دلتا h) است. ماتریس‌های سیستم را در یک m-file وارد کنید.

کد متلب:

1. پایداری

یکی از اولین کارهایی که می‌خواهیم انجام دهیم، تحلیل پایداری سیستم حلقه باز (بدون هیچ کنترلی) است. همانطور که در بخش مقدمه: تحلیل سیستم بحث شد، مقادیر ویژه ماتریس سیستم، A، (برابر با قطب‌های تابع تبدیل) پایداری را تعیین می‌کنند. مقادیر ویژه ماتریس A، مقادیری از s هستند که جواب‌های det(sI - A) = 0 می‌باشند.

کد متلب:

با بررسی، می‌توان دریافت که یکی از قطب‌ها در نیم‌صفحه سمت راست قرار دارد (یعنی دارای بخش حقیقی مثبت است)، که به این معنی است که سیستم حلقه باز ناپایدار است. برای مشاهده‌ی اینکه وقتی شرایط اولیه‌ی غیر صفر وجود دارد، چه اتفاقی برای این سیستم ناپایدار می‌افتد، خطوط زیر را به m-file خود اضافه کنید و دوباره آن را اجرا کنید:

کد متلب:

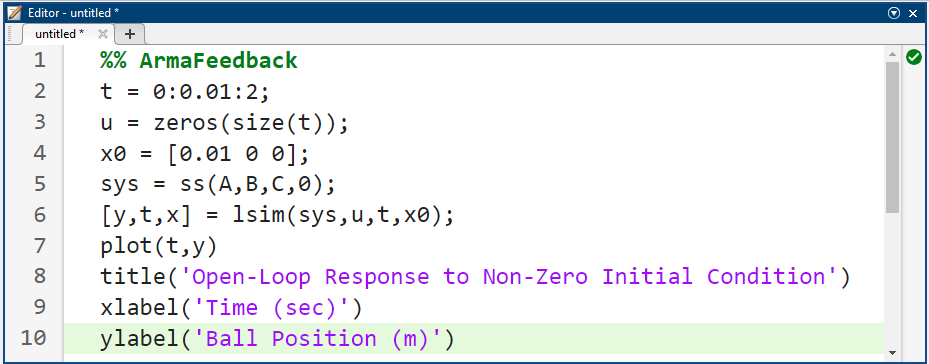
نتیجه شبیه‌سازی:

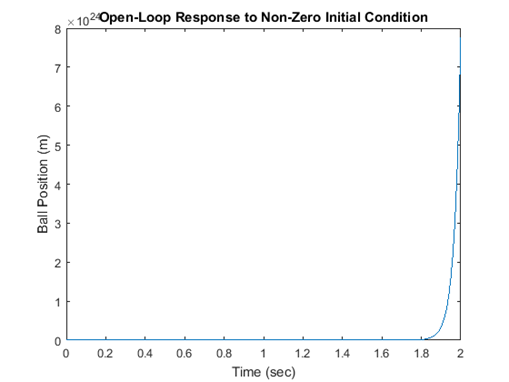
به نظر می‌رسد که فاصله بین توپ و آهنربای الکتریکی به بی‌نهایت خواهد رسید، اما احتمالاً توپ ابتدا به میز یا زمین برخورد می‌کند (و همچنین احتمالاً از محدوده‌ای که خطی‌سازی ما در آن معتبر است، خارج می‌شود).

1. کنترل‌پذیری و مشاهده‌پذیری (Controllability and Observability)

    

یک سیستم در صورتی کنترل‌پذیر است که همیشه یک ورودی کنترلی، u(t)، وجود داشته باشد که هر حالتی از سیستم را در زمان محدود به هر حالت دیگری منتقل کند. می‌توان نشان داد که یک سیستم LTI کنترل‌پذیر است اگر و تنها اگر ماتریس کنترل‌پذیری آن، C، رتبه کامل داشته باشد (یعنی اگر رتبه C = n باشد که در آن n تعداد متغیرهای حالت است). رتبه ماتریس کنترل‌پذیری یک مدل LTI را می‌توان در MATLAB با استفاده از دستورات rank(ctrb(A,B)) یا rank(ctrb(sys)) تعیین کرد

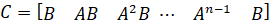
ممکن است تمام متغیرهای حالت یک سیستم، به عنوان مثال، اگر جزء در مکانی غیرقابل دسترس باشد، مستقیماً قابل اندازه‌گیری نباشند. در این موارد، لازم است مقادیر متغیرهای حالت داخلی ناشناخته فقط با استفاده از خروجی‌های موجود سیستم تخمین زده شوند. یک سیستم در صورتی قابل مشاهده است که حالت اولیه، x(t_0)، را بتوان بر اساس دانش ورودی سیستم، u(t) و خروجی سیستم، y(t)، در یک بازه زمانی محدود t_0 < t < t_f تعیین کرد. برای سیستم‌های LTI، سیستم در صورتی قابل مشاهده است که و تنها در صورتی که ماتریس مشاهده‌پذیری، O، دارای رتبه کامل باشد (یعنی اگر rank(O = n که n تعداد متغیرهای حالت است). مشاهده‌پذیری یک مدل LTI را می‌توان در متلب با استفاده از دستور rank(obsv(A,C)) یا rank(obsv(sys)) تعیین کرد.

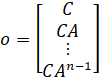
کنترل‌پذیری و مشاهده‌پذیری مفاهیم دوگانه‌ای هستند. یک سیستم (A, B) کنترل‌پذیر است اگر و تنها اگر یک سیستم (A’, B’) مشاهده‌پذیر باشد. این واقعیت هنگام طراحی یک مشاهده‌گر مفید خواهد بود، همانطور که در ادامه خواهیم دید.

1. طراحی کنترل با استفاده از جایگذاری قطب

    

بیایید با استفاده از روش جایگذاری قطب، یک کنترل‌کننده برای این سیستم بسازیم. شماتیک یک سیستم بازخورد حالت کامل در زیر نشان داده شده است. منظور از حالت کامل این است که تمام متغیرهای حالت در همه زمان‌ها برای کنترل‌کننده شناخته شده باشند. برای این سیستم، به یک حسگر برای اندازه‌گیری موقعیت توپ، حسگر دیگری برای اندازه‌گیری سرعت توپ و حسگر سومی برای اندازه‌گیری جریان در آهنربای الکتریکی نیاز داریم.

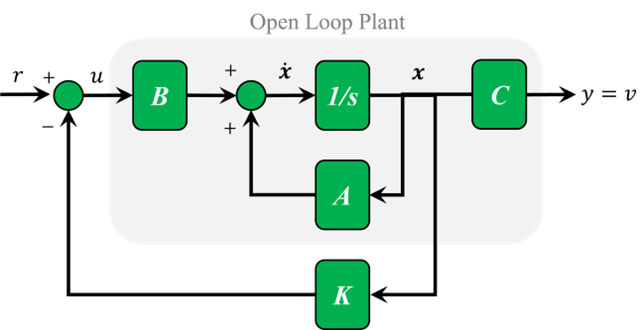
برای سادگی، فرض کنید مرجع صفر است، r = 0. ورودی عبارت است از:

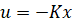
بنابراین، معادلات فضای حالت برای سیستم فیدبک حلقه بسته به صورت زیر هستند:

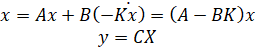
پایداری و عملکرد حوزه زمان سیستم فیدبک حلقه بسته در درجه اول توسط مکان مقادیر ویژه ماتریس (A-BK) تعیین می‌شود که برابر با قطب‌های حلقه بسته هستند. از آنجایی که ماتریس‌های A و BK هر دو ۳x۳ هستند، ۳ قطب برای سیستم وجود خواهد داشت. با انتخاب یک ماتریس بهره فیدبک حالت مناسب K، می‌توانیم این قطب‌های حلقه بسته را در هر جایی که می‌خواهیم قرار دهیم (زیرا سیستم قابل کنترل است). می‌توانیم از تابع place در متلب برای یافتن بهره فیدبک حالت، K، استفاده کنیم که قطب‌های حلقه بسته مورد نظر را فراهم می‌کند.

قبل از امتحان کردن این روش، باید تصمیم بگیریم که قطب‌های حلقه بسته را کجا می‌خواهیم قرار دهیم. فرض کنید معیارهای کنترل‌کننده زمان نشست < 0.5 ثانیه و فراجهش < 5% باشد، پس می‌توانیم سعی کنیم دو قطب غالب را در -10 +/- 10i (در zeta = 0.7 یا 45 درجه با sigma = 10 > 4.6*2) قرار دهیم. قطب سوم را می‌توانیم برای شروع در -50 قرار دهیم (به طوری که به اندازه کافی سریع باشد که تأثیر زیادی بر پاسخ نداشته باشد) و می‌توانیم بعداً آن را بسته به رفتار حلقه بسته تغییر دهیم. دستور lsim را از m-file و هر چیز بعد از آن حذف کنید، سپس خطوط زیر را به m-file خود اضافه کنید:

کد متلب:

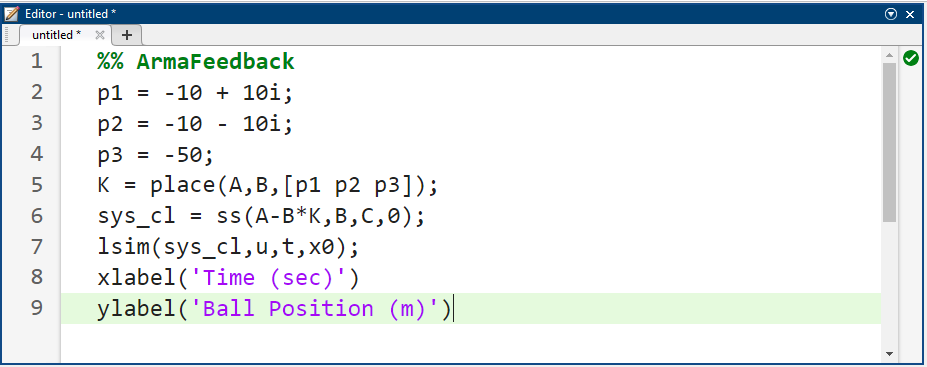
نتیجه شبیه‌سازی:

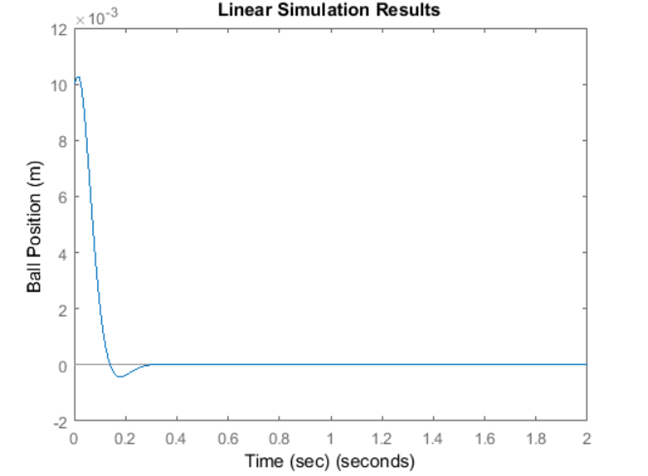
این بار، فراجهش کمتر است. برای پیشنهادات بیشتر در مورد انتخاب قطب‌های حلقه بسته مورد نظر، به کتاب درسی خود مراجعه کنید. نیروی کنترلی مورد نیاز (u) را در هر دو مورد مقایسه کنید. به طور کلی، هر چه قطب‌ها را بیشتر به سمت چپ حرکت دهید، نیروی کنترلی بیشتری مورد نیاز است.

نکته: اگر می‌خواهید دو یا چند قطب را در یک موقعیت قرار دهید، تابع place کار نخواهد کرد. می‌توانید از تابعی به نام acker استفاده کنید که به همان هدف می‌رسد (اما می‌تواند از نظر عددی کمتر خوش‌شرط باشد):

کد متلب:

1. معرفی ورودی مرجع

    

اکنون، سیستم کنترل را مطابق تعریف بالا در نظر می‌گیریم و یک ورودی پله اعمال می‌کنیم (ما مقدار کوچکی را برای پله انتخاب می‌کنیم، بنابراین در ناحیه‌ای باقی می‌مانیم که خطی‌سازی ما معتبر است). t، u و lsim را در m-file خود با موارد زیر جایگزین کنید:

کد متلب:

تنیجه شبیه‌سازی:

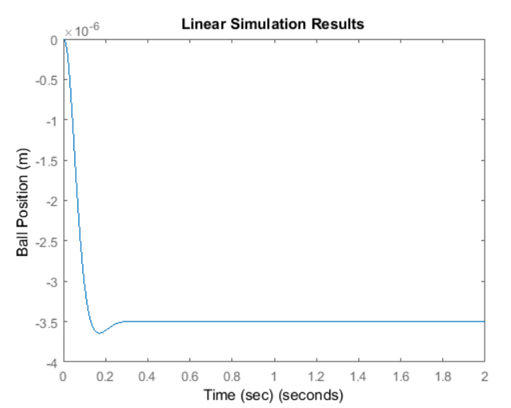
سیستم به هیچ وجه پله را به خوبی دنبال نمی‌کند؛ نه تنها اندازه آن یک نیست، بلکه به جای مثبت، منفی است. شماتیک بالا را به خاطر بیاورید، ما خروجی را با مرجع مقایسه نمی‌کنیم؛ در عوض همه حالت‌ها را اندازه‌گیری می‌کنیم، در بردار بهره K ضرب می‌کنیم و سپس این نتیجه را از مرجع کم می‌کنیم. هیچ دلیلی وجود ندارد که انتظار داشته باشیم Kx برابر با خروجی مطلوب باشد. برای رفع این مشکل، می‌توانیم ورودی مرجع را مقیاس‌بندی کنیم تا در حالت پایدار برابر با Kx شود. ضریب مقیاس، overline{N}، در شماتیک زیر نشان داده شده است:

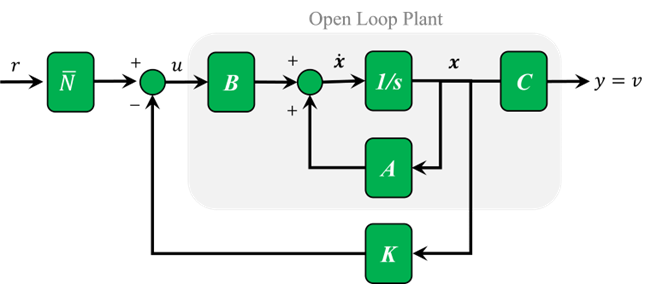
می‌توانیم N را در MATLAB با استفاده از تابع rescale محاسبه کنیم (خط کد زیر را بعد از K = ... قرار دهید).

برنامه تابع rscale در متلب:

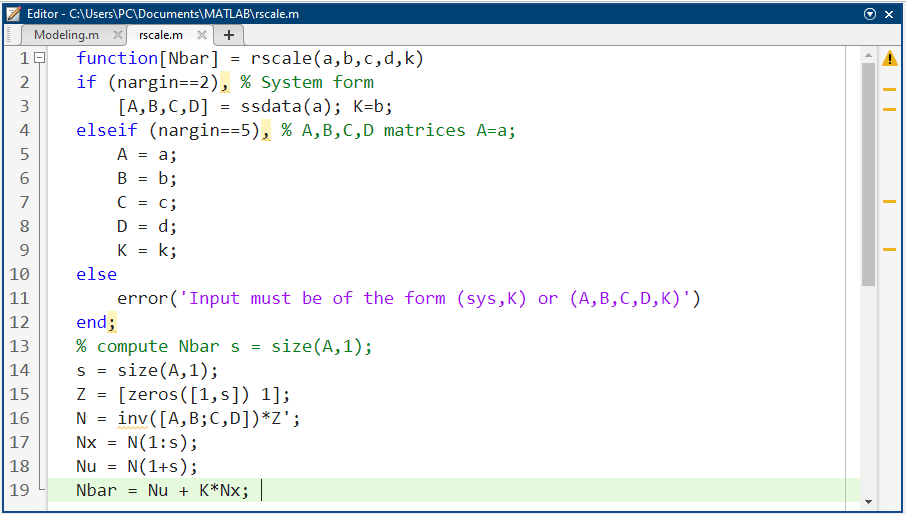
حال، اگر بخواهیم پاسخ سیستم را تحت بازخورد حالت با این مقیاس‌بندی مرجع پیدا کنیم، به سادگی به این نکته توجه می‌کنیم که ورودی در این عامل جدید، N، ضرب می‌شود:

کد متلب:

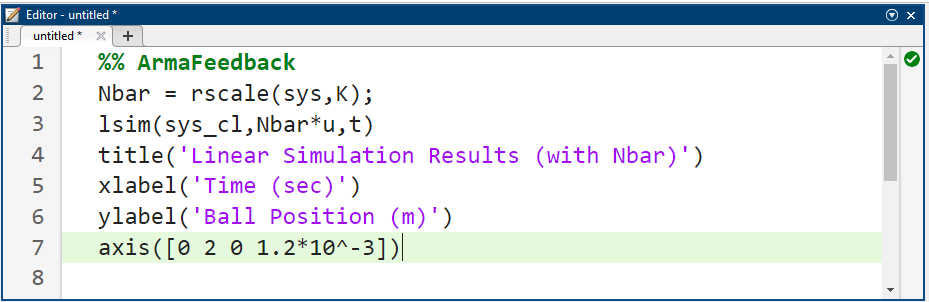
نتیجه شبیه‌سازی:

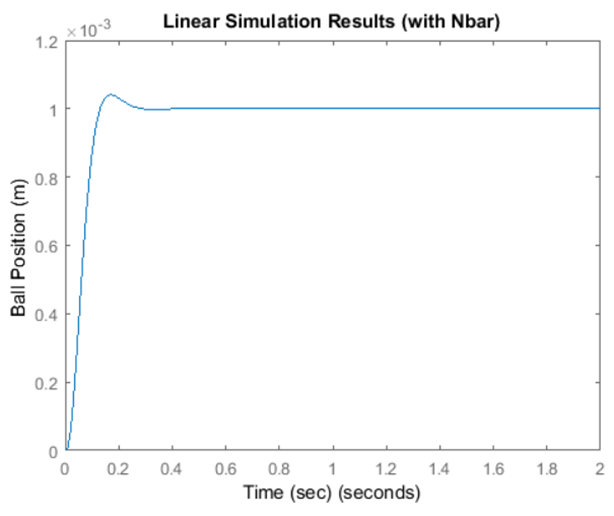
و اکنون می‌توان یک گام را به طور معقولی ردیابی کرد. توجه داشته باشید که محاسبه ضریب مقیاس‌بندی ما نیاز به دانش خوبی از سیستم دارد. اگر مدل ما خطا داشته باشد، ورودی را به مقدار نادرستی مقیاس‌بندی خواهیم کرد. یک جایگزین، مشابه آنچه با کنترل PID معرفی شد، اضافه کردن یک متغیر حالت برای انتگرال خطای خروجی است. این کار باعث اضافه شدن یک عبارت انتگرالی به کنترل‌کننده ما می‌شود که به کاهش خطای حالت پایدار معروف است.

1. طراحی رویتگر (Observer)

    

وقتی نمی‌توانیم همه متغیرهای حالت x را اندازه‌گیری کنیم (که اغلب در عمل چنین است)، می‌توانیم یک ناظر بسازیم تا آنها را تخمین بزند، در حالی که فقط خروجی y = Cx را اندازه‌گیری می‌کند. برای مثال توپ مغناطیسی، سه متغیر حالت جدید و تخمینی (hat x) را به سیستم اضافه خواهیم کرد. طرح کلی به شرح زیر است:

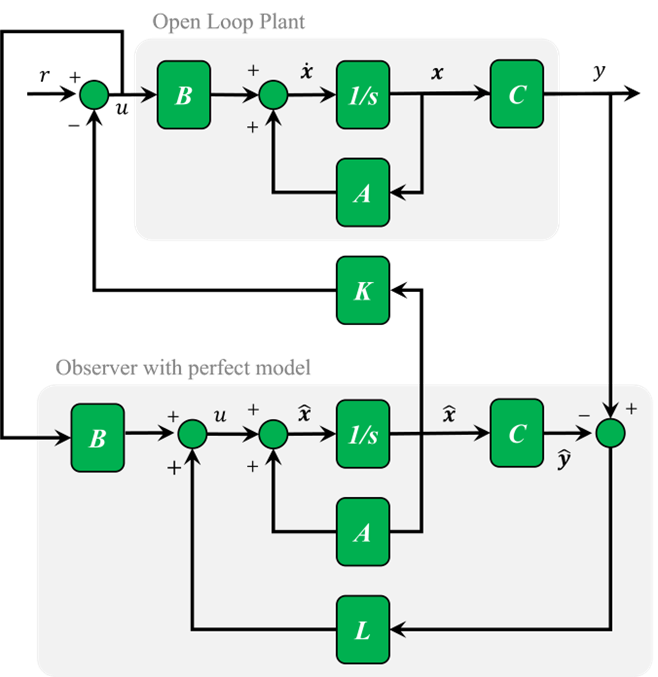
رویتگر اساساً یک کپی از سیستم است؛ ورودی یکسان و تقریباً همان معادله دیفرانسیل را دارد. یک عبارت اضافی، خروجی اندازه‌گیری شده واقعی y را با خروجی تخمینی y = C hat x مقایسه می‌کند؛ این به اصلاح حالت تخمینی y hat x کمک می‌کند و باعث می‌شود که به مقادیر حالت واقعی x نزدیک شود (اگر اندازه‌گیری حداقل خطا را داشته باشد).

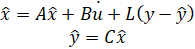
دینامیک خطای ناظر توسط قطب‌های A-LC داده شده است.

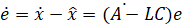
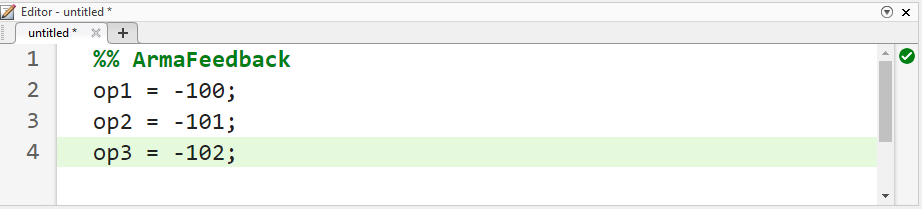
ابتدا، باید بهره‌ی ناظر L را انتخاب کنیم. از آنجایی که می‌خواهیم دینامیک ناظر بسیار سریع‌تر از خود سیستم باشد، باید قطب‌ها را حداقل پنج برابر دورتر از قطب‌های غالب سیستم در سمت چپ قرار دهیم. اگر بخواهیم از مکان استفاده کنیم، باید سه قطب ناظر را در مکان‌های مختلف قرار دهیم.

کد متلب:

به دلیل دوگانگی بین کنترل‌پذیری و مشاهده‌پذیری، می‌توانیم از همان تکنیکی که برای یافتن ماتریس کنترل استفاده می‌شود، با جایگزینی ماتریس B با ماتریس C و گرفتن ترانهاده‌های هر ماتریس استفاده کنیم:

کد متلب:

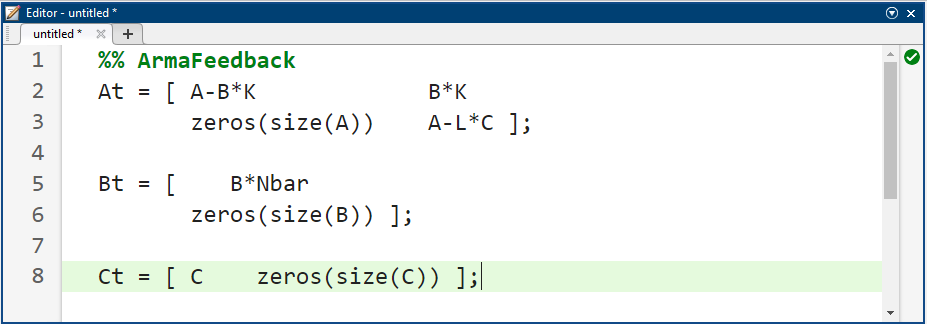
معادلات موجود در نمودار بلوکی بالا برای تخمین hat x داده شده‌اند. معمولاً معادلات ترکیبی برای سیستم به علاوه ناظر با استفاده از معادلات حالت اصلی به علاوه خطای تخمین نوشته می‌شوند: e = x - hatx. ما از حالت تخمین زده شده برای بازخورد استفاده می‌کنیم، u = -K hat x، زیرا لزوماً همه متغیرهای حالت اندازه‌گیری نمی‌شوند. پس از کمی جبر (برای جزئیات بیشتر به کتاب درسی خود مراجعه کنید)، به معادلات حالت و خطای ترکیبی برای بازخورد حالت کامل با یک ناظر می‌رسیم.

کد متلب:

برای اینکه ببینید پاسخ به یک شرط اولیه غیر صفر بدون ورودی مرجع چگونه ظاهر می‌شود، خطوط زیر را به m-file خود اضافه کنید. در اینجا فرض می‌کنیم که ناظر با یک تخمین اولیه برابر با صفر شروع می‌کند، به طوری که خطای تخمین اولیه برابر با بردار حالت اولیه، e = x، باشد.

کد متلب:

نتیجه شبیه‌سازی:

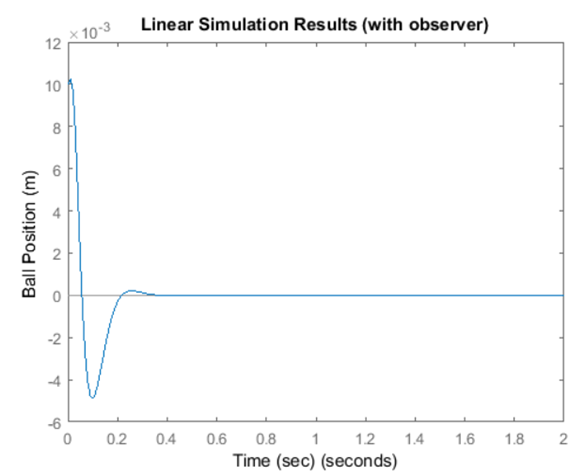
پاسخ‌های تمام متغیرهای حالت در زیر رسم شده‌اند. به یاد داشته باشید که lsim به ما x و e می‌دهد؛ برای بدست آوردن مقدار x، باید x -e را محاسبه کنیم.

کد متلب:

نتیجه شبیه‌سازی:

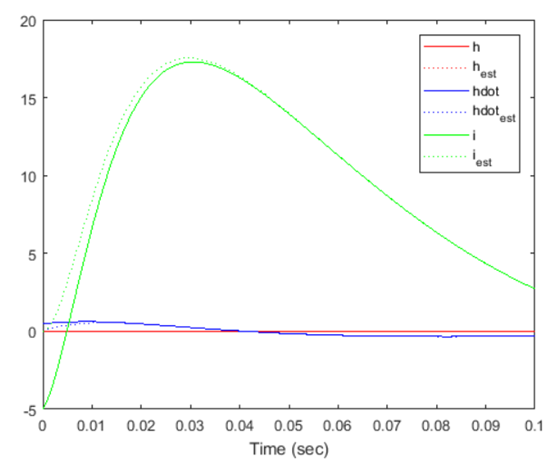
از موارد فوق، می‌توانیم ببینیم که تخمین‌های ناظر به سرعت به متغیرهای حالت واقعی همگرا می‌شوند و متغیرهای حالت را در حالت پایدار به خوبی ردیابی می‌کنند.

منابع:

C. H. Houpis, S. N. Sheldon, and J. J. D'Azzo, Linear Control System Analysis and Design, 5th ed. Boca Raton, FL: CRC Press, 2013

Y. Bavafa-Toosi, Introduction to Linear Control Systems. Amsterdam, Netherlands: Elsevier, 2017

K. Ogata, Modern Control Engineering, 5th ed. Upper Saddle River, NJ: Pearson, 2010

N. S. Nise, Control Systems Engineering, 6th ed. Hoboken, NJ: John Wiley & Sons, 2011

C.-T. Chen, Linear System Theory and Design, 3rd ed. New York, NY: Oxford University Press, 1999

G. F. Franklin, J. D. Powell, and A. Emami-Naeini, Feedback Control of Dynamic Systems, 7th ed. Boston, MA: Pearson, 2014

#کنترل_خطی #کنترل_مدرن #کنترل_مقاوم #کنترل_فازی #کنترل_کنترل_هوشمند #کنترل_دیجیتال #کنترل_پیش_بین_مبتنی_بر_مدل #کنترل_بهینه #کنترل_چند_متغییره #کنترل_کلاسیک #کنترل_اتوماتیک #کنترل_عصبی #کنترل_چند_عاملی #کنترل_شبکه‌ای #کنترل_تطبیقی #کنترل #کنترل_غیر_خطی #مهندسی_کنترل #متلب #سیمولینک #متلب_سیمولینک #تابع_تبدیل #معادلات_حالت #مدل_سازی #شبیه‌سازی #کنترل_مبتنی_بر_داده #کنترل_سیستم #سیستم #بهینه_سازی #سنسور #فیدبک #بازخورد

آکادمی آرمـــا فیدبــک