مدل سازی و طراحی کنترلر برای سیستم زاویه موتور DC با استفاده از متلب

مدل سازی و طراحی کنترلر برای سیستم زاویه موتور DC با استفاده از متلب

چکیده مطالب:

ابتدا، معادلات دینامیکی موتور DC در قالب فضای حالت ارائه شده و کنترل‌پذیری سیستم تأیید می‌شود. سپس، یک کنترل‌کننده فیدبک حالت کامل با استفاده از جایگذاری قطب طراحی می‌شود. شبیه‌سازی نشان می‌دهد که این کنترل‌کننده، خطای حالت ماندگار بزرگی در پاسخ به مرجع و اغتشاش دارد. برای رفع این مشکل، عمل انتگرالی به کنترل‌کننده اضافه می‌شود. این کار با تقویت معادلات فضای حالت و طراحی مجدد کنترل‌کننده صورت می‌گیرد. نتایج شبیه‌سازی نهایی تأیید می‌کنند که با افزودن انتگرال‌گیر، تمام معیارهای طراحی، از جمله حذف خطای حالت ماندگار در حضور اغتشاش، برآورده می‌شوند.

فهرست مطالب:

1. 1) طراحی کنترل‌کننده فیدبک حالت کامل

2) پاسخ به اغتشاش

3) افزودن عمل انتگرالی

4) منابع

از مسئله اصلی، معادلات دینامیکی به شکل فضای حالت در زیر آورده شده است.

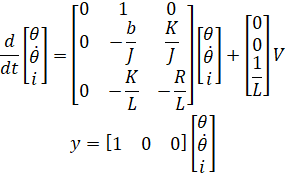
موارد فوق به شکل یک مجموعه استاندارد از معادلات فضای حالت است که در زیر توضیح داده شده است.

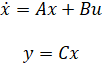
رای تنظیم اولیه مسئله و استخراج معادلات فوق، لطفاً به صفحه موقعیت موتور DC: مدل‌سازی سیستم مراجعه کنید. با مرجع پله ۱ رادیان، معیارهای طراحی به شرح زیر است:

1. 1) زمان نشست کمتر از ۰.۰۴۰ ثانیه
2. 2) فراجهش کمتر از ۱۶٪
3. 3) بدون خطای حالت ماندگار، حتی در حضور ورودی اختلال پله

ابتدا یک m-file جدید ایجاد کنید و دستورات زیر را در آن تایپ کنید (برای جزئیات دریافت این دستورات به مسئله اصلی مراجعه کنید).

کد متلب:

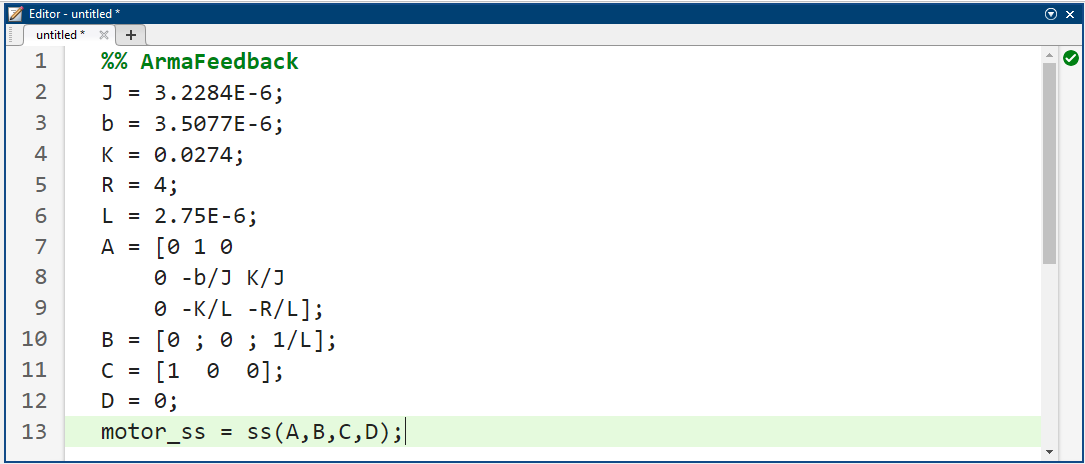
طراحی کنترل‌کننده فیدبک حالت کامل

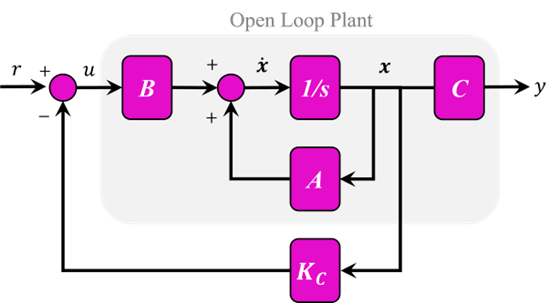
از آنجایی که اندازه‌گیری تمام متغیرهای حالت در مسئله ما بسیار آسان است (به سادگی یک آمپرمتر برای جریان، یک تاکومتر برای سرعت و یک پتانسیومتر برای موقعیت اضافه کنید)، می‌توانیم یک کنترل‌کننده فیدبک حالت کامل برای سیستم طراحی کنیم بدون اینکه نگران اضافه کردن یک ناظر باشیم. قانون کنترل برای یک سیستم فیدبک حالت کامل به شکل u = r - Kc x است. نمودار بلوکی مربوطه در زیر آورده شده است.

شکل 1: نمودار بلوکی سیستم همراه با کنترل کننده

به یاد بیاورید که چندجمله‌ای مشخصه برای این سیستم حلقه بسته، دترمینان sI -(A-B Kc) است که در آن s متغیر لاپلاس است. از آنجایی که ماتریس‌های A و B Kc هر دو ماتریس‌های ۳x۳ هستند، باید ۳ قطب برای سیستم وجود داشته باشد. این واقعیت را می‌توان با دستور دستور MATLAB تأیید کرد. اگر سیستم داده شده قابل کنترل باشد، با طراحی یک کنترل‌کننده فیدبک حالت کامل می‌توانیم این سه قطب را به هر جایی که می‌خواهیم منتقل کنیم. اینکه آیا سیستم داده شده قابل کنترل است یا خیر را می‌توان با بررسی رتبه ماتریس کنترل‌پذیری [B AB A^2B ...] تعیین کرد. دستور ctrb در متلب ماتریس کنترل‌پذیری را با توجه به A و B می‌سازد. علاوه بر این، دستور rank رتبه یک ماتریس داده شده را تعیین می‌کند، اگرچه می‌تواند از نظر عددی غیرقابل اعتماد باشد. بنابراین، از دستور det برای محاسبه دترمینان ماتریس کنترل‌پذیری استفاده خواهیم کرد که در آن یک ماتریس رتبه کامل دارای یک دترمینان غیر صفر است. دستورات زیر که در خط فرمان اجرا می‌شوند، ترتیب سیستم و قابل کنترل بودن یا نبودن آن را بررسی می‌کنند.

کد متلب:

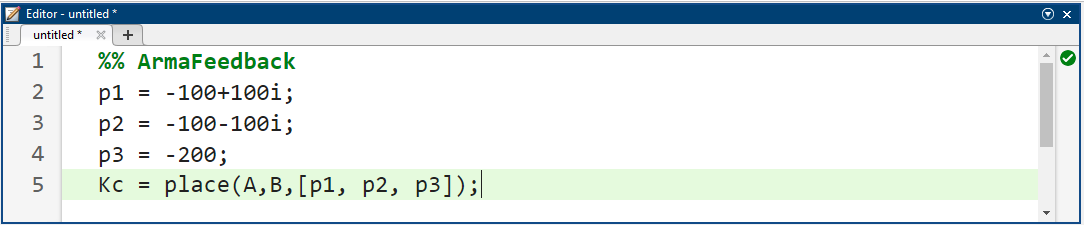
از مطالب بالا، می‌دانیم که سیستم ما کنترل‌پذیر است زیرا دترمینان ماتریس کنترل‌پذیری صفر نیست و از این رو می‌توانیم قطب‌های حلقه بسته سیستم را در هر جایی از صفحه s قرار دهیم. ابتدا قطب‌ها را در -200، -100+100i و -100-100i قرار می‌دهیم. با نادیده گرفتن اثر قطب اول (از آنجایی که سریع‌تر از دو قطب دیگر است)، قطب‌های غالب مربوط به یک سیستم مرتبه دوم با zeta = 0.5 مربوط به 16٪ فراجهش و sigma = 100 مربوط به زمان نشست 0.040 ثانیه هستند. پس از تعیین مکان قطب‌های مورد نظر، می‌توانیم از دستورات place یا acker در MATLAB برای تعیین ماتریس بهره کنترل‌کننده، Kc، برای دستیابی به این قطب‌ها استفاده کنیم. ما از دستور place استفاده خواهیم کرد زیرا از نظر عددی بهتر از acker شرطی‌سازی شده است. با این حال، اگر بخواهیم قطبی با کثرت بزرگتر از رتبه ماتریس B قرار دهیم، باید از دستور acker استفاده کنیم. کد زیر را به انتهای m-file خود اضافه کنید.

کد متلب:

با مراجعه به معادلات و شماتیک بالای صفحه، می‌بینیم که با به‌کارگیری قانون بازخورد حالت u = r - Kc x، معادلات فضای حالت به صورت زیر در می‌آیند.

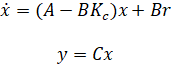
ما می‌توانیم با اضافه کردن خطوط زیر به انتهای m-file خود، پاسخ حلقه بسته به یک مرجع مرحله را تولید کنیم. m-file خود را در پنجره فرمان اجرا کنید و باید نموداری مانند آنچه در زیر نشان داده شده است، ایجاد کنید.

کد متلب:

نتیجه شبیه‌سازی:

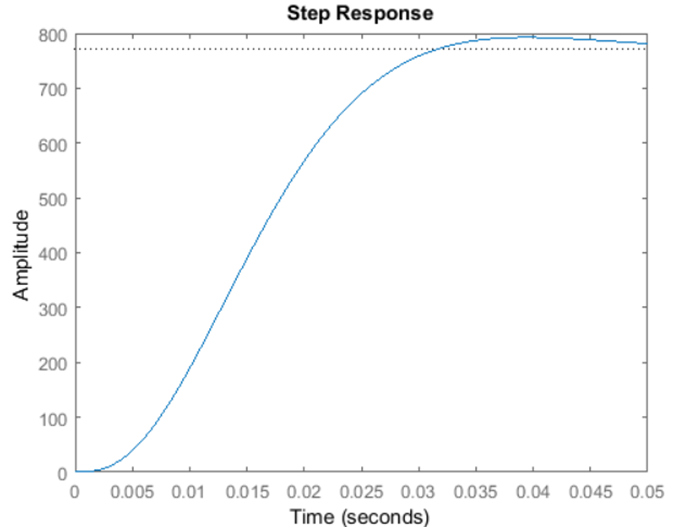
توجه داشته باشید که الزامات داده شده ما برآورده نمی‌شوند، به طور خاص، خطای حالت ماندگار بسیار بزرگ است. قبل از پرداختن به این موضوع، ابتدا به پاسخ سیستم به اغتشاش نگاهی می‌اندازیم.

پاسخ به اختلال

برای مشاهده پاسخ به اختلال سیستم، باید ورودی مناسب را به سیستم ارائه دهیم. در این حالت، یک اختلال از نظر فیزیکی گشتاور بار است که بر اینرسی موتور تأثیر می‌گذارد. این گشتاور بار به عنوان یک عبارت افزایشی در معادله حالت دوم عمل می‌کند (که مانند سایر عبارات این معادله بر J تقسیم می‌شود). ما می‌توانیم این را به سادگی با تغییر ماتریس ورودی حلقه بسته خود، B، به گونه‌ای شبیه‌سازی کنیم که در ردیف دوم 1 / J داشته باشیم، با این فرض که ورودی فعلی ما فقط اختلال است.

خطوط زیر را به m-file خود اضافه کنید و دوباره اجرا کنید.

کد متلب:

نتیجه شبیه‌سازی:

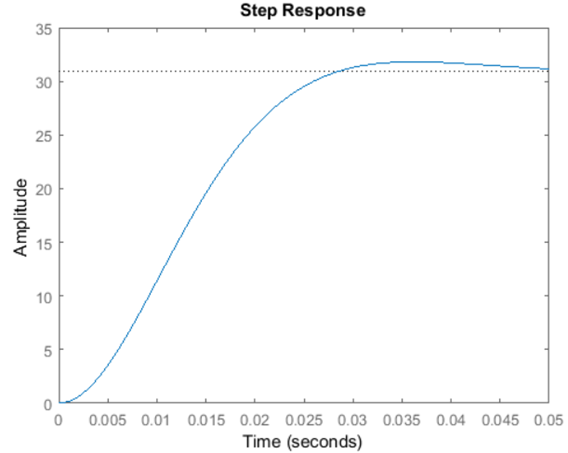
توجه داشته باشید که خطای ناشی از اختلال پله غیر صفر است. بنابراین، این مورد نیز باید جبران شود.

افزودن عمل انتگرال

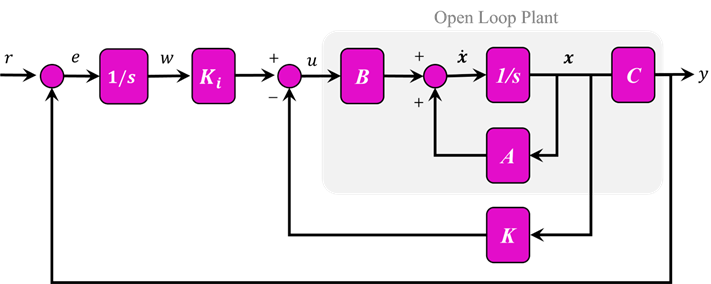
از مثال‌های قبلی می‌دانیم که اگر یک انتگرال‌گیر اضافی را به صورت سری با سیستم قرار دهیم، می‌تواند خطای حالت ماندگار ناشی از مرجع پله را حذف کند. اگر انتگرال‌گیر قبل از تزریق اختلال قرار گیرد، ورودی اختلال پله را نیز در حالت ماندگار لغو می‌کند. این امر ساختار کنترل ما را تغییر می‌دهد به طوری که اکنون شبیه نمودار بلوکی نشان داده شده در شکل زیر است.

شکل 2: نمودار بلوکی سیستم همراه با کنترل کننده و پیش جبران ساز

می‌توانیم با افزودن معادلات حالت خود به یک حالت اضافی برای انتگرال خطا که آن را با متغیر w مشخص می‌کنیم، جمع این انتگرال‌گیر را مدل‌سازی کنیم. این کار یک معادله حالت اضافی اضافه می‌کند که در آن مشتق این حالت دقیقاً برابر با خطا است، e = y - r که در آن y = تتا. این معادله در پایین ماتریس‌های ما قرار خواهد گرفت. بنابراین، مرجع r اکنون به عنوان یک ورودی اضافی برای سیستم ما ظاهر می‌شود. خروجی سیستم ثابت می‌ماند.

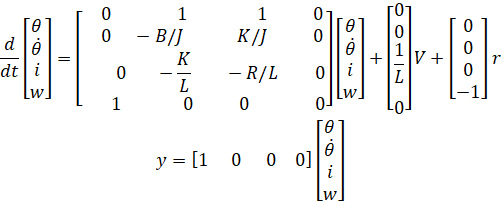
این معادلات، دینامیک سیستم را قبل از بسته شدن حلقه نشان می‌دهند. ما در این معادله، ماتریس‌های سیستم را که با حالت انتگرال‌گیر اضافی تقویت شده‌اند، با Aa، Ba، Ca و Da نشان می‌دهیم. برداری که ورودی مرجع r را ضرب می‌کند، با Br نشان داده می‌شود. ما بردار حالت سیستم تقویت‌شده را با xa نشان می‌دهیم. توجه داشته باشید که مرجع، r، بر حالت‌ها (به جز حالت انتگرال‌گیر) یا خروجی سیستم تأثیر نمی‌گذارد. این انتظار می‌رود زیرا هیچ مسیری از مرجع به ورودی سیستم، u، بدون پیاده‌سازی ماتریس بهره فیدبک حالت Kc وجود ندارد.

برای یافتن معادلات حلقه بسته، باید بررسی کنیم که ورودی، u، چگونه بر سیستم تأثیر می‌گذارد. در این حالت، دقیقاً به همان روشی که در معادلات غیر افزوده شده عمل می‌کند، بر سیستم تأثیر می‌گذارد، با این تفاوت که اکنون u = -Kc x - Ki w است. همچنین می‌توانیم این را بر حسب حالت افزوده شده خود به صورت u = -Ka xa بازنویسی کنیم که در آن Ka = [Kc Ki] است. با جایگذاری این u در معادلات بالا، معادلات حلقه بسته زیر حاصل می‌شود.

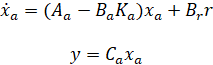
در بالا، انتگرال خطا بازخورد داده می‌شود و منجر به کاهش خطای حالت ماندگار به صفر می‌شود. حال باید کنترل‌کننده خود را طوری طراحی کنیم که بردار حالت افزوده را در نظر بگیرد. از آنجایی که باید هر قطب سیستم را قرار دهیم، قطبی را که با حالت انتگرال‌گیر اضافی مرتبط است در -300 قرار می‌دهیم که سریع‌تر از سایر قطب‌ها خواهد بود.

خطوط زیر را به m-file خود اضافه کنید که معادلات حلقه بسته ارائه شده در بالا را منعکس می‌کنند. توجه داشته باشید که از آنجایی که ماتریس انتقال حلقه بسته Aa-Ba Ka به Ba بستگی دارد، به جای Br در دستور place استفاده خواهد شد. اجرای m-file شما، نمودار نشان داده شده در زیر را تولید می‌کند.

کد متلب:

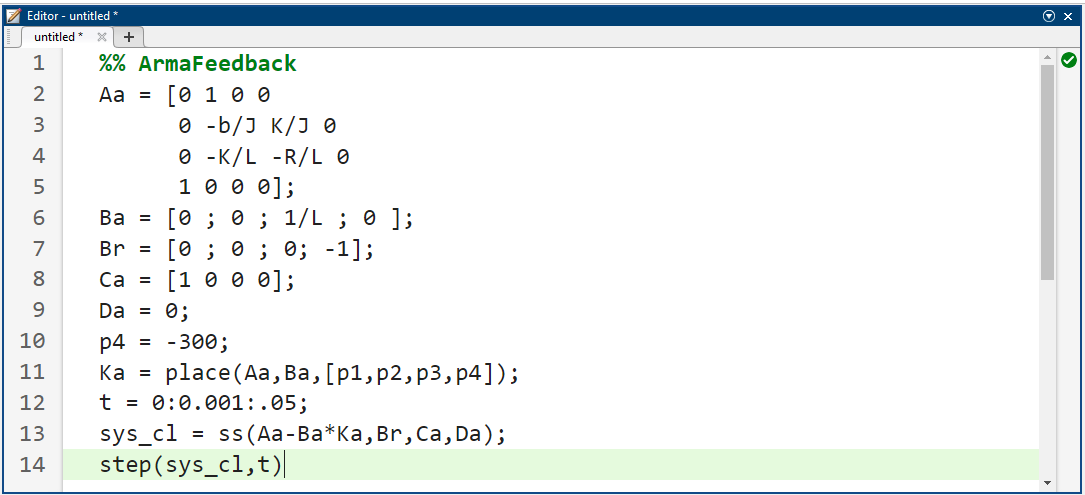
نتیجه شبیه‌سازی:

برای مشاهده پاسخ اختلال، از رویکردی مشابه با رویکرد بدون عمل انتگرال‌گیری استفاده می‌کنیم.

کد متلب:

نتیجه شبیه‌سازی:

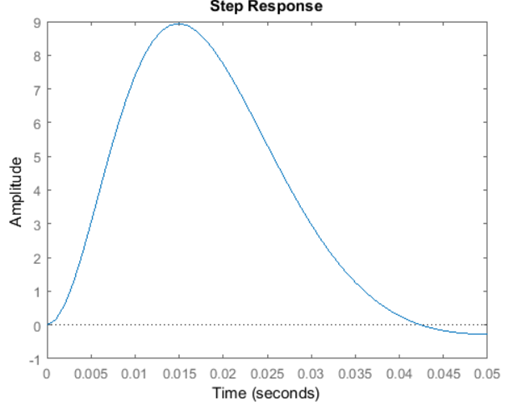
می‌توانیم ببینیم که این کنترل‌کننده تقریباً تمام مشخصات طراحی را برآورده می‌کند. زمان نشست ممکن است کمی زیاد باشد، اما با قرار دادن قطب‌های حلقه بسته کمی دورتر به سمت چپ در صفحه s مختلط، این نیاز نیز می‌تواند برآورده شود.

منابع:

C. H. Houpis, S. N. Sheldon, and J. J. D'Azzo, Linear Control System Analysis and Design, 5th ed. Boca Raton, FL: CRC Press, 2013

Y. Bavafa-Toosi, Introduction to Linear Control Systems. Amsterdam, Netherlands: Elsevier, 2017

K. Ogata, Modern Control Engineering, 5th ed. Upper Saddle River, NJ: Pearson, 2010

N. S. Nise, Control Systems Engineering, 6th ed. Hoboken, NJ: John Wiley & Sons, 2011

C.-T. Chen, Linear System Theory and Design, 3rd ed. New York, NY: Oxford University Press, 1999

G. F. Franklin, J. D. Powell, and A. Emami-Naeini, Feedback Control of Dynamic Systems, 7th ed. Boston, MA: Pearson, 2014

#کنترل_خطی #کنترل_مدرن #کنترل_مقاوم #کنترل_فازی #کنترل_کنترل_هوشمند #کنترل_دیجیتال #کنترل_پیش_بین_مبتنی_بر_مدل #کنترل_بهینه #کنترل_چند_متغییره #کنترل_کلاسیک #کنترل_اتوماتیک #کنترل_عصبی #کنترل_چند_عاملی #کنترل_شبکه‌ای #کنترل_تطبیقی #کنترل #کنترل_غیر_خطی #مهندسی_کنترل #متلب #سیمولینک#متلب_سیمولینک #تابع_تبدیل #معادلات_حالت #مدل_سازی #شبیه‌سازی #کنترل_مبتنی_بر_داده #کنترل_سیستم #سیستم #بهینه_سازی #سنسور #فیدبک #بازخورد

آکادمی آرمـــا فیدبــک