مدلسازی و طراحی کنترلر برای سیستم زاویه گشتاور هواپیما با استفاده از متلب
چکیده مطالب:
ابتدا، معادلات فیزیکی حرکت هواپیما (با فرض پرواز در حالت کروز) ارائه و خطیسازی میشوند. سپس، مدل سیستم به دو صورت تابع تبدیل و فضای حالت نمایش داده شده و الزامات طراحی برای پاسخ پله سیستم تعریف میگردد. تحلیل پاسخ حلقه باز نشان میدهد که سیستم ناپایدار است، اما با افزودن یک بازخورد ساده، پایدار میشود، گرچه معیارهای عملکردی را برآورده نمیکند. در ادامه، کنترلپذیری سیستم تأیید میشود که امکان طراحی کنترلکننده با روشهای فضای حالت را فراهم میسازد. از روش تنظیم خطی درجه دوم (LQR) برای یافتن ماتریس بهره کنترل استفاده میشود که باعث بهبود زمانهای صعود و نشست و فراجهش سیستم میشود، اما خطای حالت پایدار قابل توجهی باقی میماند. در نهایت، برای حذف خطای حالت پایدار، یک پیشجبرانساز به سیستم کنترل فیدبک حالت کامل اضافه میشود. این پیشجبرانساز ورودی مرجع را مقیاسبندی میکند و نتایج شبیهسازی نشان میدهند که با این رویکرد، تمامی الزامات طراحی برآورده شدهاند.
فهرست مطالب:
مدلسازی سیستم:
معادلات فیزیکی و سیستم
تابع انتقال و مدلهای فضای حالت
الزامات طراحی
نمایش با متلب
تحلیل پایدار سیستم مورد مطالعه:
پاسخ حلقه باز
پاسخ حلقه بسته
روشهای فضای حالت برای طراحی کنترلکننده:
کنترلپذیری
طراحی کنترل از طریق جایگذاری قطب
تنظیم خطی درجه دوم
افزودن پیش جبرانسازی
معادلات فیزیکی و سیستم
معادلات حاکم بر حرکت یک هواپیما، مجموعهای بسیار پیچیده از شش معادله دیفرانسیل کوپل غیرخطی هستند. با این حال، تحت فرضیات خاصی، میتوان آنها را از هم جدا کرد و به معادلات طولی و جانبی خطیسازی نمود. زاویه چرخش هواپیما توسط دینامیک طولی تعیین میشود. در این مثال، یک خلبان خودکار طراحی خواهیم کرد که زاویه چرخش هواپیما را کنترل میکند.
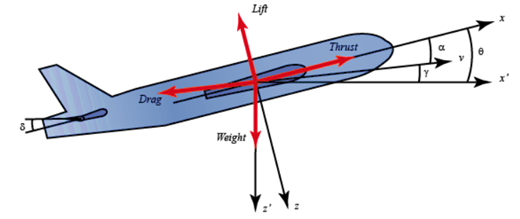
فرض میکنیم که هواپیما در ارتفاع و سرعت ثابت در حالت کروز پایدار قرار دارد؛ بنابراین، نیروهای رانش، پسا، وزن و بالابر در جهتهای x و y یکدیگر را متعادل میکنند. همچنین فرض میکنیم که تغییر در زاویه گام، سرعت هواپیما را تحت هیچ شرایطی تغییر نمیدهد (غیرواقعی است اما مسئله را کمی ساده میکند). تحت این فرضیات، معادلات حرکت طولی هواپیما را میتوان به صورت زیر نوشت.
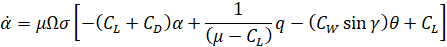
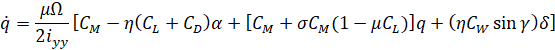
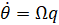
برای این سیستم، ورودی، دلتای زاویه انحراف بالابر و خروجی، تتای زاویه گام هواپیما خواهد بود.
مدلهای تابع انتقال و فضای حالت
قبل از یافتن مدلهای تابع انتقال و فضای حالت، بیایید برخی از مقادیر عددی را برای سادهسازی معادلات مدلسازی نشان داده شده در بالا وارد کنیم:
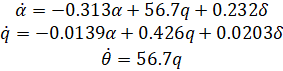
این مقادیر از دادههای یکی از هواپیماهای تجاری بوئینگ گرفته شدهاند.
تابع تبدیل
برای یافتن تابع تبدیل سیستم فوق، باید تبدیل لاپلاس معادلات مدلسازی فوق را بدست آوریم. به یاد داشته باشید که هنگام یافتن تابع تبدیل، شرایط اولیه باید صفر فرض شود. تبدیل لاپلاس معادلات فوق در زیر نشان داده شده است.
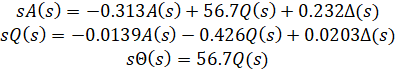
پس از چند مرحله جبر، باید تابع تبدیل زیر را بدست آورید.
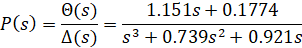
فضای حالت
با توجه به اینکه معادلات مدلسازی فوق از قبل به شکل متغیر حالت هستند، میتوانیم آنها را به صورت ماتریسهایی که در زیر نشان داده شده است، بازنویسی کنیم.
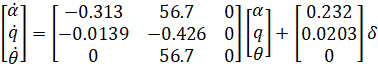
از آنجایی که خروجی ما زاویه گام است، معادله خروجی به صورت زیر است.
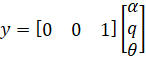
الزامات طراحی
مرحله بعدی انتخاب برخی معیارهای طراحی است. در این مثال، ما یک کنترلکننده فیدبک طراحی خواهیم کرد تا در پاسخ به دستور پلهای زاویه گام، زاویه گام واقعی کمتر از 10٪ از حد مجاز تجاوز کند، زمان خیزش کمتر از 2 ثانیه، زمان نشست کمتر از 10 ثانیه و خطای حالت پایدار کمتر از 2٪ داشته باشد. به عنوان مثال، اگر مرجع 0.2 رادیان (11 درجه) باشد، زاویه گام تقریباً از 0.22 رادیان تجاوز نمیکند، در عرض 2 ثانیه از 0.02 رادیان به 0.18 رادیان افزایش مییابد، در عرض 10 ثانیه به حدود 2٪ از مقدار حالت پایدار خود میرسد و در حالت پایدار بین 0.196 تا 0.204 رادیان تثبیت میشود.
به طور خلاصه، الزامات طراحی به شرح زیر است.
فراجهش کمتر از 10٪
زمان خیزش کمتر از 2 ثانیه
زمان نشست کمتر از 10 ثانیه
خطای حالت پایدار کمتر از 2٪
نمایش تابع تبدیل و معادلات حالت در متلب:
اکنون، ما آماده نمایش سیستم با استفاده از متلب هستیم. اجرای کد زیر در پنجره فرمان، مدل تابع تبدیل حلقه باز شرح داده شده در بالا را تولید میکند.
کد متلب:

برای تولید مدل فضای حالت که در بالا توضیح داده شد، به جای آن، دستورات زیر را در خط فرمان وارد کنید.
کد متلب:
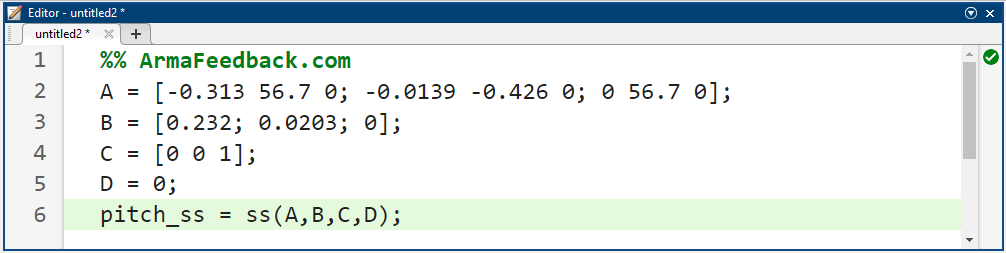
از مسئله اصلی، معادلات دینامیکی در حوزه لاپلاس و تابع تبدیل حلقه باز دینامیک گام هواپیما عبارتند از:
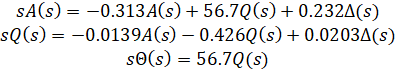
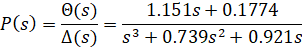
برای مرجع پله، معیارهای طراحی به شرح زیر است:
فراجهش کمتر از 10٪
زمان خیزش کمتر از 2 ثانیه
زمان نشست کمتر از 10 ثانیه
خطای حالت پایدار کمتر از 2٪
پاسخ حلقه باز
ابتدا یک m-file جدید ایجاد کنید و دستورات زیر را در آن تایپ کنید.
کد متلب:

حالا بیایید ببینیم سیستم حلقه باز جبران نشده چگونه عمل میکند. به طور خاص، ما از دستور step در متلب برای تجزیه و تحلیل پاسخ پله حلقه باز استفاده خواهیم کرد که در آن ورودی را برای نمایش ورودی زاویه بالابر (دلتا) 0.2 رادیان (11 درجه) مقیاسبندی کردهایم. دستورات زیر را به انتهای m-file اضافه کنید و آن را در پنجره فرمان متلب اجرا کنید تا نمودار مربوطه که در زیر نشان داده شده است را دریافت کنید.
کد متلب:
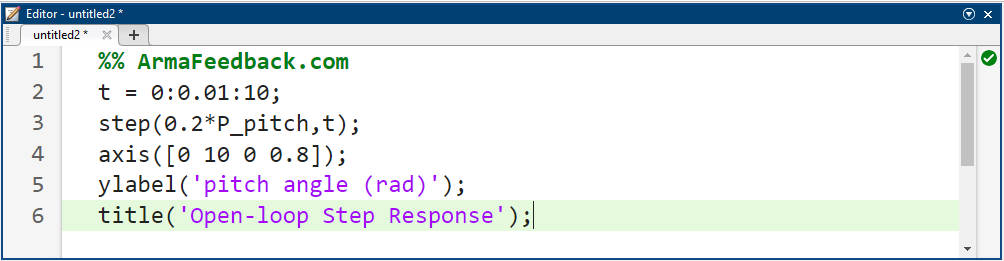
نتیجه شبیهسازی:
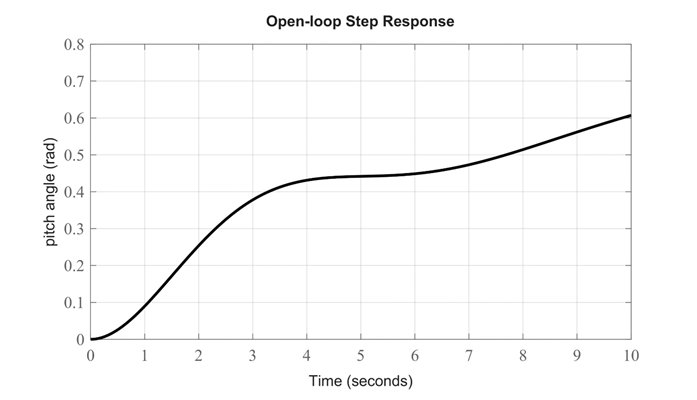
از نمودار بالا، میبینیم که پاسخ حلقه باز به هیچ وجه معیارهای طراحی را برآورده نمیکند. در واقع، پاسخ حلقه باز ناپایدار است. پایداری یک سیستم را میتوان با بررسی قطبهای تابع تبدیل تعیین کرد که در آن قطبها را میتوان با استفاده از دستور pole در متلب، همانطور که در زیر نشان داده شده است، شناسایی کرد.
کد متلب:
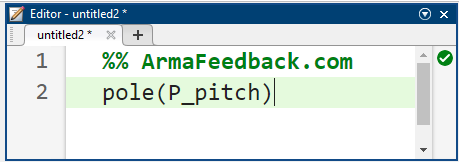
همانطور که در این تابع نشان داده شده است، یکی از قطبهای تابع تبدیل حلقه باز روی محور موهومی قرار دارد در حالی که دو قطب دیگر در نیمه چپ صفحه s مختلط هستند. وجود یک قطب روی محور موهومی نشان میدهد که پاسخ آزاد سیستم به صورت نامحدود رشد نخواهد کرد، اما به صفر نیز کاهش نخواهد یافت. اگرچه پاسخ آزاد به صورت نامحدود رشد نخواهد کرد، اما سیستمی با یک قطب روی محور موهومی میتواند با دریافت ورودی، حتی زمانی که ورودی محدود باشد، به صورت نامحدود رشد کند. این واقعیت با آنچه قبلاً دیدهایم مطابقت دارد. در این مورد خاص، قطب در مبدا مانند یک انتگرالگیر رفتار میکند. بنابراین، هنگامی که به سیستم یک ورودی پلهای داده میشود، خروجی آن به همان روشی که انتگرال یک ثابت با بزرگتر شدن حد بالایی انتگرال به بینهایت رشد میکند، همچنان به بینهایت رشد میکند.
پاسخ حلقه بسته
به منظور پایدارسازی این سیستم و در نهایت برآورده کردن الزامات طراحی داده شده، یک کنترلکننده فیدبک اضافه خواهیم کرد. شکل زیر معماری کنترلی را که به کار خواهیم گرفت نشان میدهد.
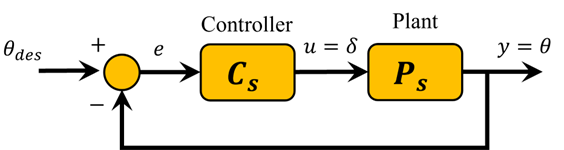
تابع تبدیل حلقه بسته برای مورد فوق با کنترلر C(s) که به سادگی برابر با یک قرار میگیرد، میتواند با استفاده از دستور فیدبک متلب مطابق شکل زیر تولید شود.
کد متلب:
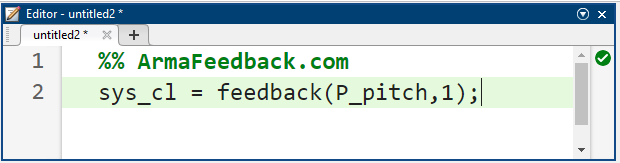
پاسخ پله مربوطه را میتوان با اضافه کردن دستورات بالا و زیر به m-file خود تولید کرد. توجه داشته باشید که پاسخ به گونهای مقیاسبندی میشود که این واقعیت را مدلسازی کند که مرجع زاویه گام، یک گام 0.2 رادیان (11 درجه) است. اجرای m-file شما در خط فرمان، نمودار نشان داده شده در زیر را ایجاد میکند که در آن میتوان حاشیهنویسیهای مربوط به زمان صعود، زمان نشست و مقدار نهایی را از منوی کلیک راست در زیر Characteristics به نمودار اضافه کرد.
کد متلب:
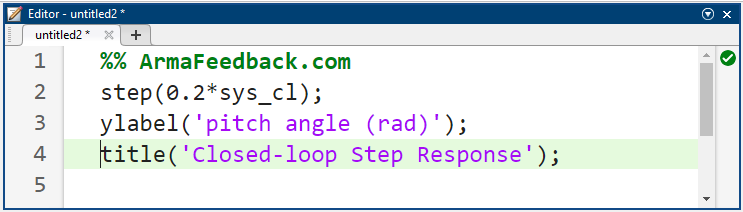
نتیجه شبیهسازی:
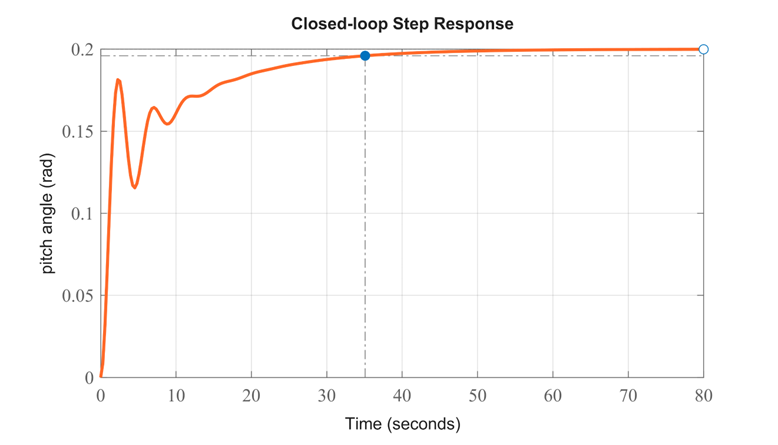
با بررسی پاسخ پله حلقه بسته فوق، افزودن بازخورد، سیستم را پایدار کرده است. در واقع، به نظر میرسد خطای حالت ماندگار به صفر رسیده و هیچ جهشی در پاسخ وجود ندارد، اگرچه الزامات زمان صعود و زمان نشست برآورده نشدهاند. ویژگی پاسخ پله حاصل با محل قطبها و صفرهای تابع تبدیل سیستم، به روشی مشابه با نحوه تعیین ویژگیهای پایداری سیستم، نشان داده میشود. دستورات pole و zero در متلب میتوانند برای آشکار کردن قطبها و صفرهای تابع تبدیل حلقه بسته، همانطور که در زیر نشان داده شده است، استفاده شوند.
کد متلب:
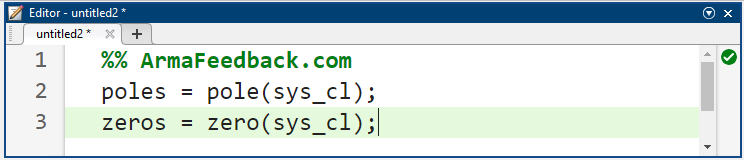
نتایج فوق نشان میدهد که تابع تبدیل حلقه بسته از مرتبه سوم با صفر است. اکثر روابطی که برای پیشبینی ویژگی پاسخ پله یک سیستم با آنها آشنا هستیم، یک سیستم مرتبه دوم استاندارد با میرایی کم و بدون صفر را فرض میکنند. بنابراین، نمیتوانیم برای این سیستم به این روابط تکیه کنیم. با این حال، میتوانیم خروجی را به حوزه زمان برگردانیم تا یک تابع زمانی برای پاسخ سیستم ایجاد کنیم تا بینشی در مورد چگونگی تأثیر قطبها و صفرهای تابع تبدیل حلقه بسته بر پاسخ سیستم به دست آوریم. با فرض اینکه تابع تبدیل حلقه بسته به شکل Y(s) / R(s) باشد، خروجی Y(s) در حوزه لاپلاس به صورت زیر محاسبه میشود که در آن R(s) یک پله با بزرگی 0.2 است.
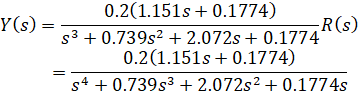
سپس میتوانیم یک بسط کسر جزئی انجام دهیم تا این عبارت را به جملات سادهتری بشکنیم که امیدواریم آنها را تشخیص دهیم و بتوانیم از حوزه لاپلاس به حوزه زمان برگردانیم. ابتدا از دستور zpk در متلب برای فاکتورگیری صورت و مخرج Y(s) خروجی خود به جملات سادهتر استفاده خواهیم کرد.
کد متلب:
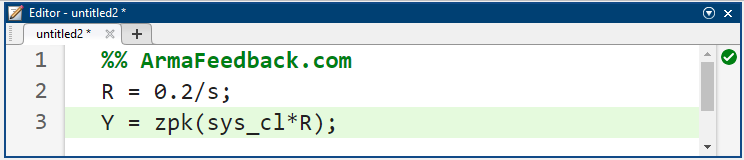
بر اساس موارد فوق، مخرج خروجی Y(s) ما را میتوان به یک عبارت مرتبه اول برای قطب حقیقی تابع تبدیل، یک عبارت مرتبه دوم برای قطبهای مزدوج مختلط تابع تبدیل و یک قطب در مبدا برای ورودی پله تجزیه کرد. بنابراین، مطلوب است که Y(s) را مطابق شکل زیر بسط دهیم.
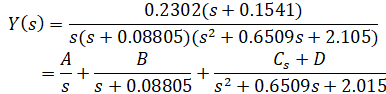
مقادیر خاص ثابتهای A، B، C و D را میتوان با محاسبه دستی یا با استفاده از دستور residue در متلب برای انجام بسط کسر جزئی، همانطور که در زیر نشان داده شده است، تعیین کرد. در اینجا، سینتکس به صورت [r,p,k] = residue(num,den) است که در آن num و den به ترتیب آرایههایی حاوی ضرایب صورت و مخرج تابع لاپلاس در حال بسط هستند. توجه داشته باشید که آرایه مخرج شامل یک جاینگهدار صفر است زیرا هیچ جمله ثابتی در مخرج Y(s) وجود ندارد.
کد متلب:

در عبارت بالا، r آرایهای شامل باقیماندههای بسط کسر جزئی، یعنی ضرایب صورت در بسط، است. آرایه p شامل قطبهای سیستم است که در آن مرتبه با مرتبه باقیماندهها در r مطابقت دارد. عبارت مستقیم k در این مورد خالی است، همانطور که در حالت کلی نیز همینطور خواهد بود، زیرا چندجملهای صورت عموماً مرتبه کوچکتری نسبت به چندجملهای مخرج خواهد داشت. بر اساس مطالب فوق، ضرایب A و B در بسط ما به ترتیب برابر با 0.2 و -0.0881 هستند. ضرایب C و D را میتوان با ترکیب عبارات مربوط به قطبهای مزدوج مختلط در یک عبارت واحد، همانطور که در زیر نشان داده شده است، تعیین کرد.
کد متلب:

بر اساس موارد فوق، C = -0.1121 و D = -0.08071 و بسط کسر جزئی حاصل را میتوان به صورت زیر بیان کرد.
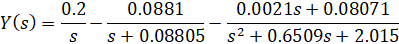
با استفاده از جدول تبدیل لاپلاس، میتوان از تبدیل لاپلاس معکوس عبارت بالا برای تولید عبارت حوزه زمان مربوطه که در زیر نشان داده شده است، استفاده کرد. اگر جعبه ابزار ریاضی نمادین (Symbolic Math) را به متلب اضافه کرده باشید، میتوانید از دستور laplace برای انجام معکوسسازی استفاده کنید.
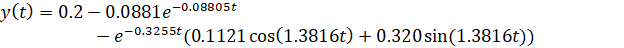
با بررسی موارد فوق، هر جمله متناظر با یک قطب Y(s) است که در آن بخش حقیقی قطب، واپاشی (یا رشد) نمایی آن مد را توصیف میکند و بخش موهومی قطب متناظر با فرکانس نوسان مد است. اثر صفرها تغییر ضرایب ضرب هر یک از جملات است. به عبارت دیگر، صفرها بر سهم نسبی هر یک از مدها تأثیر میگذارند. مثال بالا به ارائه بینشی در مورد چگونگی نشان دادن رفتار متناظر سیستم توسط قطبها و صفرها در حوزه لاپلاس در حوزه زمان کمک میکند.
وارد کردن کد زیر در پنجره فرمان متلب، نمودار نشان داده شده در زیر را ایجاد میکند که (در داخل گرد کردن) با نمودار تولید شده با استفاده از دستور step در بالا مطابقت دارد.
کد متلب:
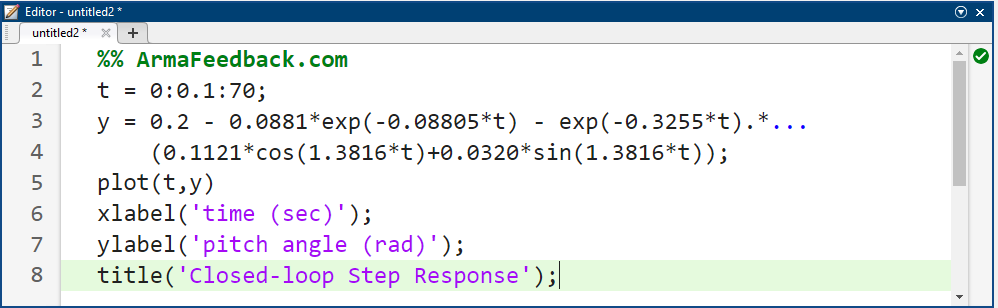
نتیجه شبیهسازی:
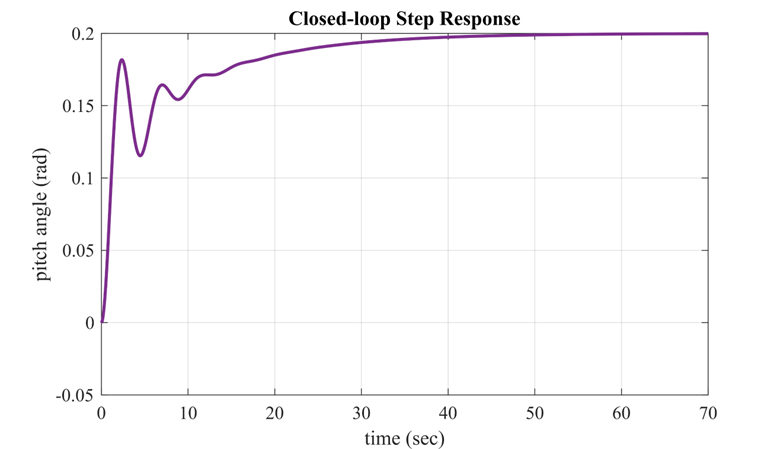
نمودار بالا دوباره نشان میدهد که این سیستم حلقه بسته، الزامات طراحی داده شده را برآورده نمیکند. صفحات بعدی این مثال، چندین تکنیک طراحی کنترلکننده را شرح میدهد که سیستمهای حلقه بستهای تولید میکنند که رفتار سیستم مورد نظر را ایجاد میکنند.
مدل فضای حالت سیستم به صورت زیر استخراج شد:
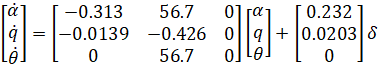
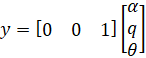
که در آن ورودی دلتای زاویه انحراف بالابر و خروجی تتای زاویه گام هواپیما است. معادلات فوق با فرم فضای حالت خطی عمومی مطابقت دارند.
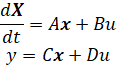
برای مرجع پله ۰.۲ رادیان، معیارهای طراحی به شرح زیر است:
فراجهش کمتر از ۱۰٪
زمان خیزش کمتر از ۲ ثانیه
زمان نشست کمتر از ۱۰ ثانیه
خطای حالت پایدار کمتر از ۲٪
در این صفحه، ما یک تکنیک طراحی کنترلکننده فضای حالت را اعمال خواهیم کرد. به طور خاص، ما تلاش خواهیم کرد تا قطبهای حلقه بسته سیستم را با طراحی کنترلکنندهای که کنترل خود را بر اساس حالتهای سیستم محاسبه میکند، قرار دهیم.
کنترلپذیری (Controllability)
برای اعمال تکنیکهای طراحی کنترلکننده فضای حالت، ابتدا باید یک ویژگی مهم، یعنی کنترلپذیری، را تأیید کنیم. ویژگی کنترلپذیری برای تضمین این که ما اختیار داریم وضعیت سیستم را به هر جایی که دوست داریم هدایت کنیم، ضروری است. این مربوط به توانایی قرار دادن قطبهای حلقه بسته سیستم در هر جایی از صفحه s مختلط است.
برای اینکه سیستم کاملاً کنترلپذیر حالت باشد،
ماتریس کنترلپذیری:
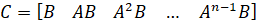
باید رتبه n داشته باشد. رتبه یک ماتریس تعداد سطرها (یا ستونهای) مستقل خطی است. عدد n مربوط به تعداد متغیرهای حالت سیستم است. اضافه کردن جملات اضافی به ماتریس کنترلپذیری با توانهای بالاتر ماتریس A، رتبه ماتریس کنترلپذیری را افزایش نمیدهد، زیرا این جملات اضافی فقط ترکیبات خطی جملات قبلی خواهند بود.
از آنجایی که ماتریس کنترلپذیری ما ۳x۳ است، رتبه ماتریس باید ۳ باشد. دستور rank در متلب میتواند رتبه این ماتریس را به شما بدهد. یک m-file جدید ایجاد کنید و دستورات زیر را در آن وارد کنید. اجرای این m-file در پنجره فرمان متلب، خروجی زیر را تولید خواهد کرد.
کد متلب:
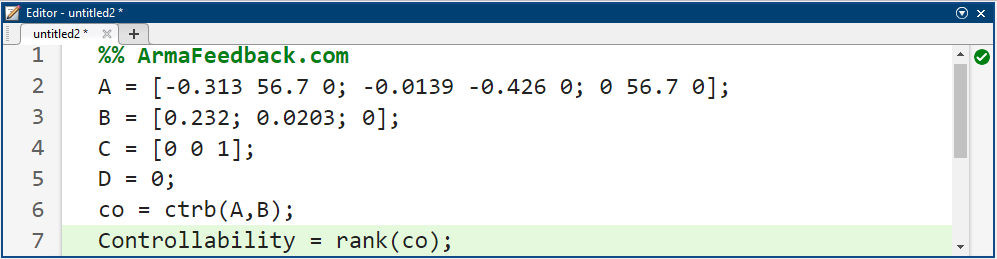
بنابراین، سیستم ما کاملاً کنترلپذیر حالت است زیرا ماتریس کنترلپذیری رتبه ۳ دارد.
طراحی کنترل از طریق جایگذاری قطب
شماتیک یک سیستم کنترل فیدبک حالت کامل در زیر نشان داده شده است (با D = 0).
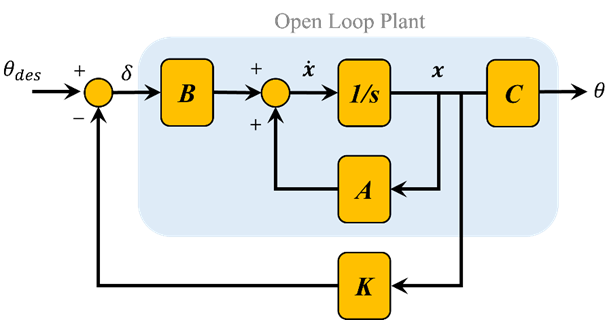
که در آن،
K = ماتریس بهره کنترل
x = [آلفا، q، تتا]' = بردار حالت
![]() = مرجع (r)
= مرجع (r)
delta = (![]() - K x) = ورودی کنترل (u)
- K x) = ورودی کنترل (u)
theta = خروجی (y)
با مراجعه مجدد به معادلات فضای حالت در بالای صفحه، میبینیم که با جایگزینی قانون بازخورد حالت delta = (theta_des - K x) به جای delta، به رابطه زیر میرسیم.
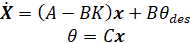
بر اساس موارد فوق، ماتریس A - BK دینامیک حلقه بسته سیستم ما را تعیین میکند. به طور خاص، ریشههای دترمینان ماتریس [sI - (A - BK)] قطبهای حلقه بسته سیستم هستند. از آنجایی که دترمینان [sI - (A - BK)] یک چندجملهای مرتبه سوم است، میتوانیم سه قطب را قرار دهیم و از آنجایی که سیستم ما کاملاً قابل کنترل حالت است، میتوانیم قطبها را در هر جایی که دوست داریم قرار دهیم. از صفحه مقدمه: روشهای فضای حالت برای طراحی کنترلکننده به یاد بیاورید که میتوان از تکنیک "جایگذاری قطب" برای یافتن ماتریس بهره کنترل K برای قرار دادن قطبهای حلقه بسته در مکانهای مورد نظر استفاده کرد. توجه داشته باشید که این قانون بازخورد فرض میکند که تمام متغیرهای حالت در بردار x اندازهگیری میشوند، حتی اگر تتا تنها خروجی ما باشد. اگر اینگونه نباشد، باید یک ناظر برای تخمین سایر متغیرهای حالت طراحی شود.
از مطالب بالا میدانیم که میتوانیم قطبهای حلقه بسته سیستم را در هر جایی که میخواهیم قرار دهیم. سوالی که باقی میماند این است که آنها را کجا باید قرار دهیم؟ اگر یک سیستم استاندارد مرتبه اول یا دوم داشته باشیم، روابطی خواهیم داشت که مکان قطبها را مستقیماً به ویژگیهای پاسخ پله مرتبط میکنند و میتوانیم از این روابط برای قرار دادن قطبها به منظور برآورده کردن نیازهای داده شده خود استفاده کنیم. اگر یک سیستم مرتبه بالاتر یا صفر داشته باشیم، این فرآیند دشوارتر میشود. در یک سیستم مرتبه بالاتر، یک رویکرد این است که قطبهای مرتبه بالاتر را ۵ تا ۱۰ برابر دورتر از قطبهای غالب در سمت چپ صفحه مختلط قرار دهیم، در نتیجه آنها سهم ناچیزی در پاسخ گذرا خواهند داشت. بررسی اثر صفرها با استفاده از رویکرد جایگذاری قطب برای کنترل دشوارتر است. محدودیت دیگر این رویکرد جایگذاری قطب این است که به صراحت عوامل دیگری مانند میزان تلاش کنترلی مورد نیاز را در نظر نمیگیرد.
تنظیم خطی درجه دوم
ما از تکنیکی به نام روش تنظیمکننده خطی درجه دوم (LQR) برای تولید "بهترین" ماتریس بهره K استفاده خواهیم کرد، بدون اینکه صریحاً تصمیم بگیریم قطبهای حلقه بسته را در مکانهای خاصی قرار دهیم. این نوع تکنیک کنترل، خطای سیستم و تلاش کنترلی را بر اساس هزینهای که طراح مشخص میکند و اهمیت نسبی به حداقل رساندن خطاها و به حداقل رساندن تلاش کنترلی را تعریف میکند، به طور بهینه متعادل میکند. در مورد مسئله تنظیمکننده، فرض میشود که مرجع صفر است. بنابراین، در این مورد، بزرگی خطا برابر با بزرگی حالت است. لطفاً برای جزئیات بیشتر به کتاب درسی کنترل خود مراجعه کنید. برای استفاده از این روش LQR، باید دو پارامتر را تعریف کنیم: ماتریس وزنی هزینه حالت (Q) و ماتریس وزنی کنترل (R). برای سادگی، ماتریس وزنی کنترلی برابر با 1 (R = 1) و ماتریس هزینه حالت (Q) برابر با pC'C را انتخاب میکنیم. استفاده از بردار C از معادله خروجی به این معنی است که ما فقط آن حالتها را در خروجی در تعریف هزینه خود در نظر خواهیم گرفت. در این حالت، تتا تنها متغیر حالت در خروجی است. ضریب وزنی (p) به منظور اصلاح پاسخ پله تغییر خواهد کرد. در این حالت، R یک اسکالر است زیرا ما یک سیستم ورودی واحد داریم.
اکنون آمادهایم تا ماتریس کنترل (K) را با استفاده از دستور lqr در متلب پیدا کنیم. ابتدا ضریب وزنی (p) را برابر با ۲ در نظر میگیریم. دستورات زیر را به m-file خود اضافه کنید و آن را در پنجره فرمان متلب اجرا کنید.
کد متلب:
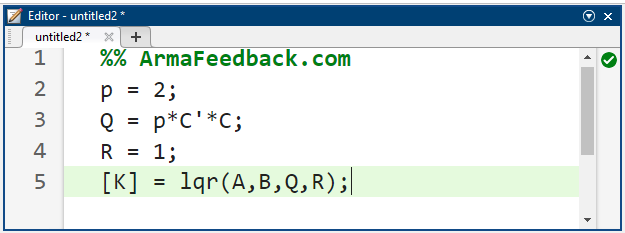
به ساختار ماتریس وزنی Q و ماتریس بهره حاصل از آن K توجه کنید. با توجه به معادلات حالت حلقه بسته داده شده در بالا با فرض یک قانون کنترل با مرجع غیر صفر، دلتا = تتا_دس - Kx)، میتوانیم پاسخ پله حلقه بسته را با اضافه کردن دستورات زیر به m-file خود و اجرای آن در پنجره فرمان متلب تولید کنیم. توجه داشته باشید که پاسخ برای مدلسازی این واقعیت که مرجع زاویه گام یک پله 0.2 رادیان (11 درجه) است، مقیاسبندی میشود. سپس پاسخ پله نشان داده شده در زیر باید تولید شود.
کد متلب:
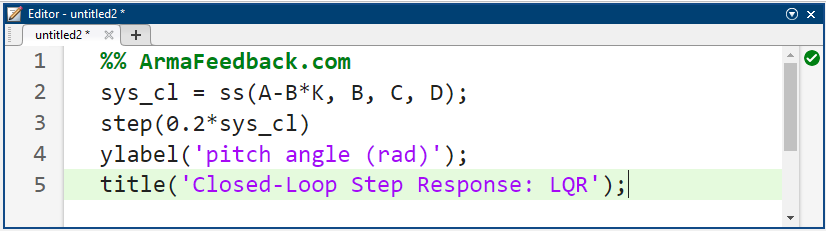
نتیجه شبیهسازی:
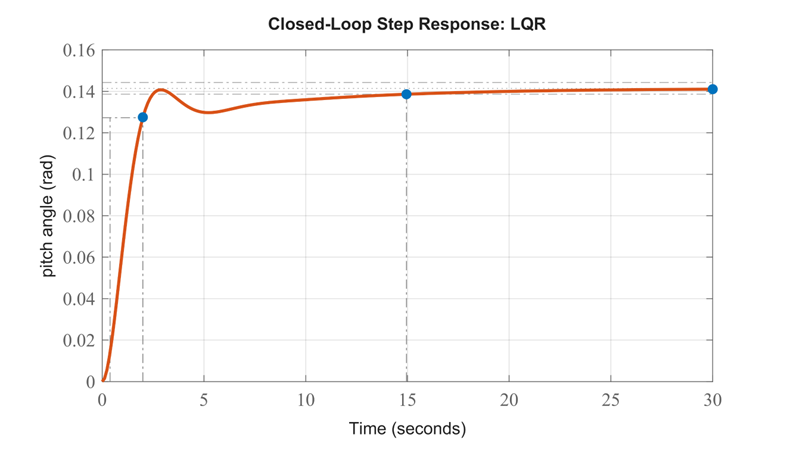
بررسی موارد فوق نشان میدهد که پاسخ بسیار کند است. میتوانیم با وزندهی بیشتر به اهمیت خطا نسبت به اهمیت تلاش کنترلی، عملکرد سیستم خود را سریعتر کنیم. به طور خاص، این کار را میتوان با افزایش ضریب وزنی p انجام داد. پس از کمی آزمون و خطا، به مقدار p = 50 رسیدیم. کد m-file خود را به صورت زیر تغییر دهید و سپس در خط فرمان اجرا کنید تا پاسخ مرحله زیر را تولید کند.
کد متلب:
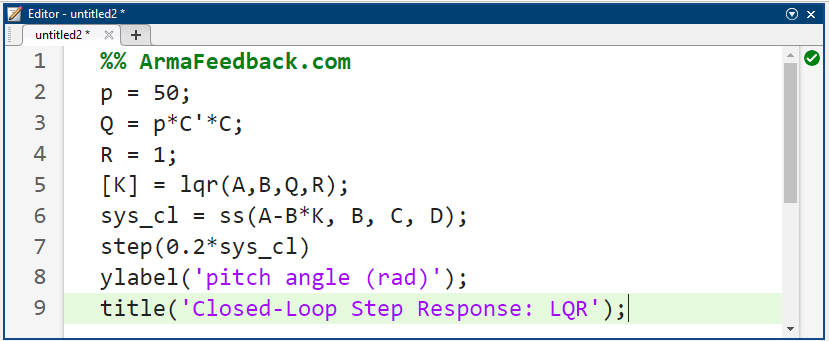
نتیجه شبیهسازی:
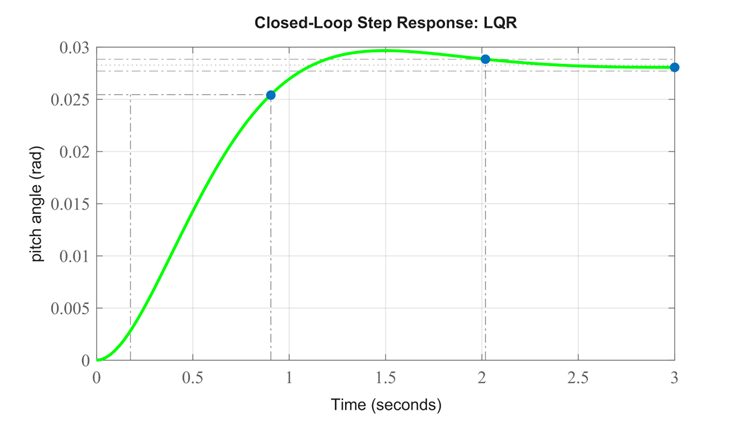
بررسی موارد فوق نشان میدهد که زمان صعود، فراجهش و زمان نشست رضایتبخش هستند. با این حال، خطای حالت پایدار زیادی وجود دارد. یک راه برای اصلاح این مشکل، معرفی یک پیش جبرانساز (overlineN) برای مقیاسبندی خروجی کلی است.
افزودن پیشجبرانسازی
برخلاف سایر روشهای طراحی، سیستم فیدبک حالت کامل، خروجی را با مرجع مقایسه نمیکند؛ در عوض، تمام حالتهای ضربشده در ماتریس کنترل (Kx) را با مرجع مقایسه میکند (به طرح شماتیک نشان داده شده در بالا مراجعه کنید). بنابراین، نباید انتظار داشته باشیم که خروجی برابر با مرجع فرمان داده شده باشد. برای به دست آوردن خروجی مطلوب، میتوانیم ورودی مرجع را طوری مقیاسبندی کنیم که خروجی در حالت پایدار با مرجع برابر باشد. این کار را میتوان با معرفی یک ضریب مقیاسبندی پیشجبرانساز به نام overlineN انجام داد. طرح شماتیک اولیه سیستم فیدبک حالت ما با ضریب مقیاسبندی (overlineN) در زیر نشان داده شده است.
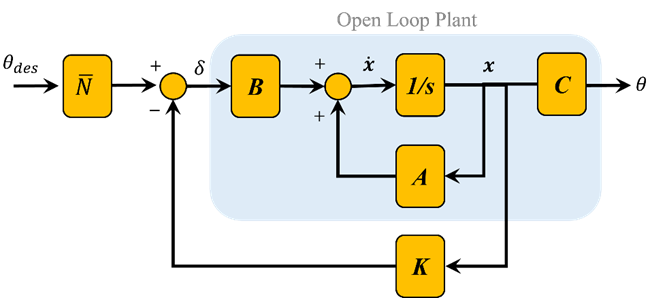
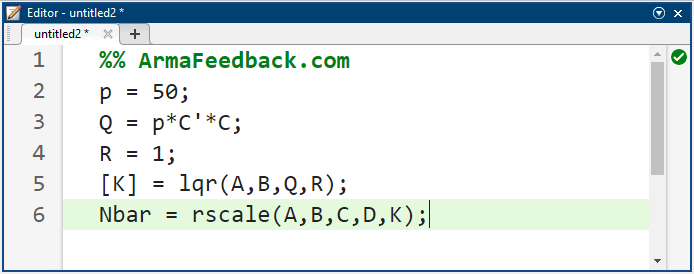
ما به راحتی میتوانیم overlineN را از تابع rscale.m در متلب پیدا کنیم. از آنجایی که rscale.m یک تابع تعریفشده توسط کاربر است، باید تابع را در دایرکتوری خود کپی و ذخیره کنید. برای کمک بیشتر در استفاده از توابع تعریفشده توسط کاربر، به صفحه تابع مراجعه کنید. پس از ذخیره فایل rscale.m در دایرکتوری خود، کد m-file خود را به صورت زیر تغییر دهید و آن را در پنجره فرمان متلب اجرا کنید.
کد متلب:
با اضافه کردن کد زیر و اجرای مجدد m-file، پاسخی که در زیر نشان داده شده است، تولید خواهد شد.
کد متلب:
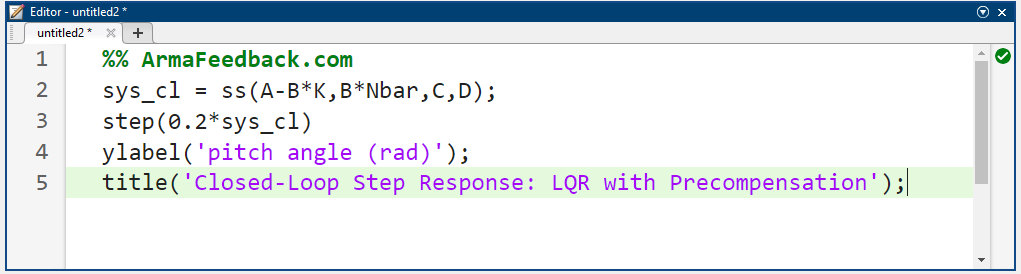
نتیجه شبیهسازی:
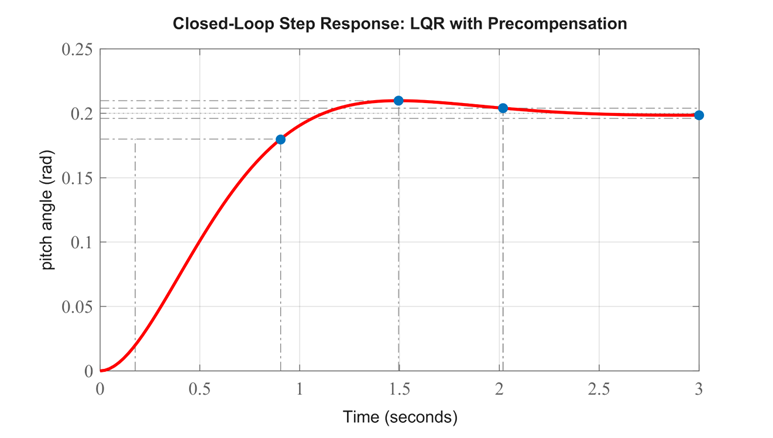
اکنون خطای حالت ماندگار حذف شده و تمام الزامات طراحی برآورده شده است.
توجه داشته باشید که پیش جبرانساز overlineN به کار رفته در بالا بر اساس مدل نیروگاه محاسبه میشود و علاوه بر این، پیش جبرانساز خارج از حلقه بازخورد قرار دارد. بنابراین، اگر در مدل خطایی (یا اختلالات ناشناخته) وجود داشته باشد، پیش جبرانساز آنها را اصلاح نمیکند و خطای حالت پایدار وجود خواهد داشت. ممکن است به یاد داشته باشید که اضافه کردن کنترل انتگرالی نیز میتواند برای حذف خطای حالت پایدار، حتی در صورت وجود عدم قطعیت مدل و اختلالات پلهای، استفاده شود. برای مثالی از نحوه پیادهسازی کنترل انتگرالی در تنظیمات فضای حالت، به صفحه موقعیت موتور DC: روشهای فضای حالت برای طراحی کنترلکننده مراجعه کنید. مزیت استفاده از کنترل انتگرالی این است که خطا ابتدا باید قبل از اینکه بتوان آن را اصلاح کرد، ایجاد شود، بنابراین، سیستم ممکن است در پاسخ دادن کند باشد. از سوی دیگر، پیش جبرانساز قادر است با استفاده از دانش مدل نیروگاه، جبران حالت پایدار را پیشبینی کند. یک تکنیک مفید، ترکیب پیش جبرانساز با کنترل انتگرالی برای بهرهبرداری از مزایای هر رویکرد است.
منابع:
C. H. Houpis, S. N. Sheldon, and J. J. D'Azzo, Linear Control System Analysis and Design, 5th ed. Boca Raton, FL: CRC Press, 2013
Y. Bavafa-Toosi, Introduction to Linear Control Systems. Amsterdam, Netherlands: Elsevier, 2017
K. Ogata, Modern Control Engineering, 5th ed. Upper Saddle River, NJ: Pearson, 2010
N. S. Nise, Control Systems Engineering, 6th ed. Hoboken, NJ: John Wiley & Sons, 2011
C.-T. Chen, Linear System Theory and Design, 3rd ed. New York, NY: Oxford University Press, 1999
G. F. Franklin, J. D. Powell, and A. Emami-Naeini, Feedback Control of Dynamic Systems, 7th ed. Boston, MA: Pearson, 2014
#کنترل_خطی #کنترل_مدرن #کنترل_مقاوم #کنترل_فازی #کنترل_کنترل_هوشمند #کنترل_دیجیتال #کنترل_پیش_بین_مبتنی_بر_مدل #کنترل_بهینه #کنترل_چند_متغییره #کنترل_کلاسیک #کنترل_اتوماتیک #کنترل_عصبی #کنترل_چند_عاملی #کنترل_شبکهای #کنترل_تطبیقی #کنترل #کنترل_غیر_خطی #مهندسی_کنترل #متلب #سیمولینک#متلب_سیمولینک #تابع_تبدیل #معادلات_حالت #مدل_سازی #شبیهسازی #کنترل_مبتنی_بر_داده #کنترل_سیستم #سیستم #بهینه_سازی #سنسور #فیدبک #بازخورد#طراحی