مدلسازی و کنترل سیستم سرعت موتور DC با استفاده از نرم افزار متلب
فهرست مطالب
مدلسازی سیستم
- تنظیمات فیزیکی
- معادلات سیستم
- الزامات طراحی
طراحی کنترل کننده
طراحی کنترلکننده فیدبک حالت کامل
افزودن یک پیش جبرانساز
منابع
روابط حاکم بر موتور DC
یک محرک رایج در سیستمهای کنترل، موتور DC است. این موتور مستقیماً حرکت چرخشی را فراهم میکند و با اتصال به چرخها یا درامها و کابلها، میتواند حرکت انتقالی را نیز فراهم کند. مدار معادل الکتریکی آرمیچر و نمودار جسم آزاد روتور در شکل زیر نشان داده شده است.
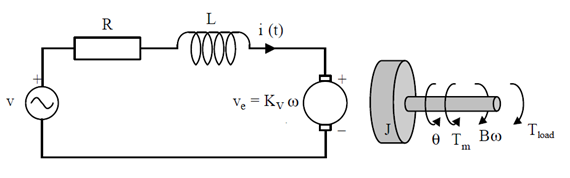
برای این مثال، فرض میکنیم که ورودی سیستم، منبع ولتاژ (V) اعمال شده به آرمیچر موتور است، در حالی که خروجی، سرعت چرخش محور (نقطه تتا) است. روتور و محور صلب فرض شدهاند. همچنین یک مدل اصطکاک ویسکوز فرض میکنیم، یعنی گشتاور اصطکاکی متناسب با سرعت زاویهای محور است.
پارامترهای فیزیکی برای این مثال ما عبارتند از:
(J) ممان اینرسی روتور 0.01 kg.m^2
(b) ثابت اصطکاک ویسکوز موتور 0.1 N.m.s
(Ke) ثابت نیروی محرکه الکتریکی 0.01 V/rad/sec
(Kt) ثابت گشتاور موتور 0.01 N.m/Amp
(R) مقاومت الکتریکی 1 اهم
(L) اندوکتانس الکتریکی 0.5 H
معادلات سیستم
به طور کلی، گشتاور تولید شده توسط یک موتور DC متناسب با جریان آرمیچر و قدرت میدان مغناطیسی است. در این مثال فرض میکنیم که میدان مغناطیسی ثابت است و بنابراین، گشتاور موتور فقط با جریان آرمیچر i با ضریب ثابت K_t متناسب است، همانطور که در معادله زیر نشان داده شده است. به این موتور، موتور کنترل شده با آرمیچر گفته میشود.
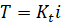
نیروی محرکه الکتریکی معکوس، e، با سرعت زاویهای شفت با ضریب ثابت K_e متناسب است.
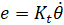
در واحدهای SI، ثابتهای گشتاور موتور و نیروی محرکه معکوس (Back emf) با هم برابرند، یعنی Kt = Ke، بنابراین، از K برای نمایش ثابت گشتاور موتور و ثابت نیروی محرکه معکوس استفاده خواهیم کرد. از تصویر بالا، میتوانیم معادلات حاکم زیر را بر اساس قانون دوم نیوتن و قانون ولتاژ کیرشهف استخراج کنیم.
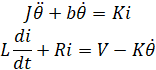
.
تابع تبدیل
با اعمال تبدیل لاپلاس، معادلات مدلسازی فوق را میتوان بر حسب متغیر لاپلاس s بیان کرد.
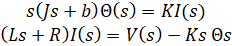
با حذف I(s) بین دو معادله بالا، به تابع تبدیل حلقه باز زیر میرسیم که در آن سرعت چرخش به عنوان خروجی و ولتاژ آرمیچر به عنوان ورودی در نظر گرفته میشود.
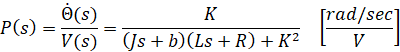
فضای حالت
در فرم فضای حالت، معادلات حاکم فوق را میتوان با انتخاب سرعت چرخش و جریان الکتریکی به عنوان متغیرهای حالت بیان کرد. مجدداً ولتاژ آرمیچر به عنوان ورودی و سرعت چرخش به عنوان خروجی انتخاب میشود.
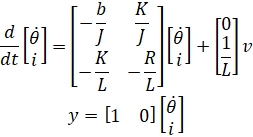
الزامات طراحی
ابتدا در نظر بگیرید که موتور جبران نشده ما در حالت پایدار برای ولتاژ ورودی ۱ ولت با سرعت ۰.۱ رادیان بر ثانیه میچرخد (این موضوع در صفحه سرعت موتور DC: تحلیل سیستم که در آن پاسخ حلقه باز سیستم شبیهسازی شده است، نشان داده شده است). از آنجایی که اساسیترین الزام یک موتور این است که با سرعت مطلوب بچرخد، ما نیاز داریم که خطای حالت پایدار سرعت موتور کمتر از ۱٪ باشد. یکی دیگر از الزامات عملکرد برای موتور ما این است که به محض روشن شدن، به سرعت حالت پایدار خود شتاب بگیرد. در این حالت، ما میخواهیم زمان تثبیت آن کمتر از ۲ ثانیه باشد. همچنین، از آنجایی که سرعت بیشتر از مرجع ممکن است به تجهیزات آسیب برساند، ما میخواهیم پاسخ پلهای با فراجهش کمتر از ۵٪ داشته باشیم. به طور خلاصه، برای یک فرمان پلهای واحد در سرعت موتور، خروجی سیستم کنترل باید الزامات زیر را برآورده کند.
زمان نشست کمتر از ۲ ثانیه
فراجهش کمتر از ۵٪
خطای حالت پایدار کمتر از ۱٪
نمایش تابع تبدیل موتور DC در متلب
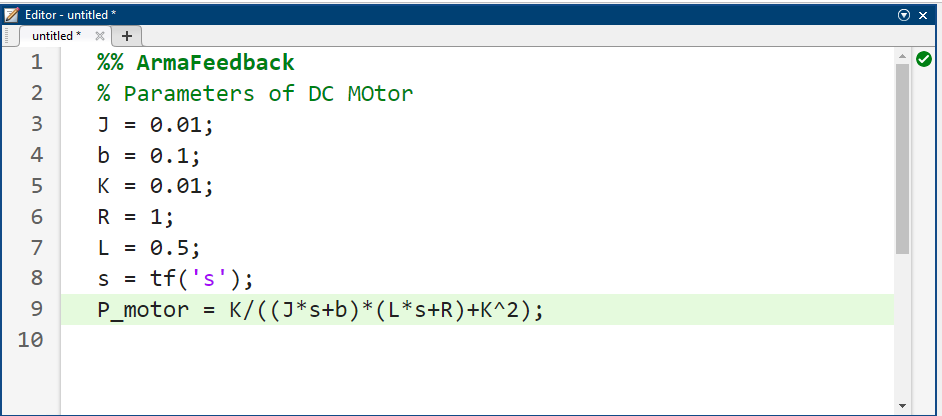
میتوانیم تابع تبدیل حلقه باز موتور فوق را در متلب با تعریف پارامترها و تابع تبدیل به صورت زیر نمایش دهیم. اجرای این کد در پنجره فرمان، خروجی نشان داده شده در زیر را تولید میکند.
کد متلب:
نمایش فضای حالت موتور DC در متلب
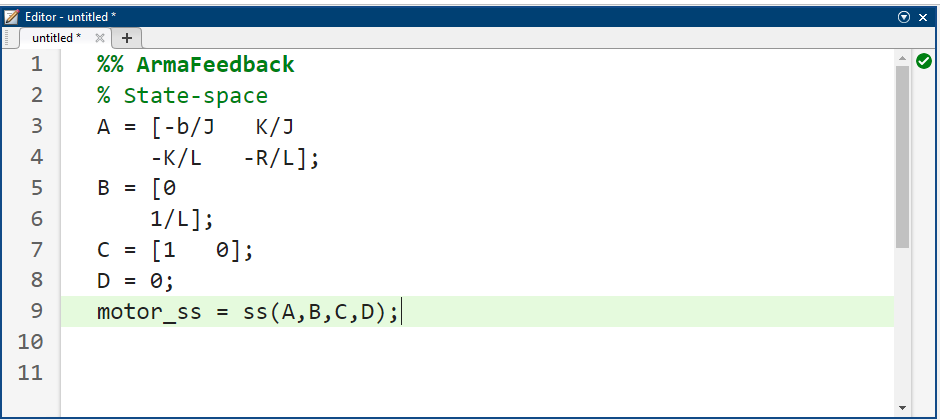
همچنین میتوانیم سیستم را با استفاده از معادلات فضای حالت نمایش دهیم. دستورات اضافی متلب زیر، یک مدل فضای حالت از موتور ایجاد میکنند و هنگام اجرا در پنجره فرمان متلب، خروجی نشان داده شده در زیر را تولید میکنند.
کد متلب:
طراحی کنترل کننده برای موتور DC در متلب
از مسئله اصلی، معادلات دینامیکی به شکل فضای حالت در زیر آورده شده است.
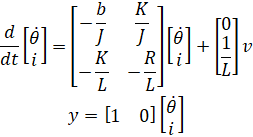
برای تنظیم اولیه مسئله و استخراج معادلات فوق، لطفاً به صفحه «سرعت موتور DC: مدلسازی سیستم» مراجعه کنید. این معادلات فضای حالت، فرم استاندارد نشان داده شده در زیر را دارند که در آن بردار حالت x = نقطه تتا i ^T و ورودی u = V است.
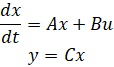
برای مرجع پله ۱ رادیان بر ثانیه، معیارهای طراحی به شرح زیر است:
- 1) زمان نشست کمتر از ۲ ثانیه
2) فراجهش کمتر از ۵٪
3) خطای مرحله پایدار کمتر از ۱٪
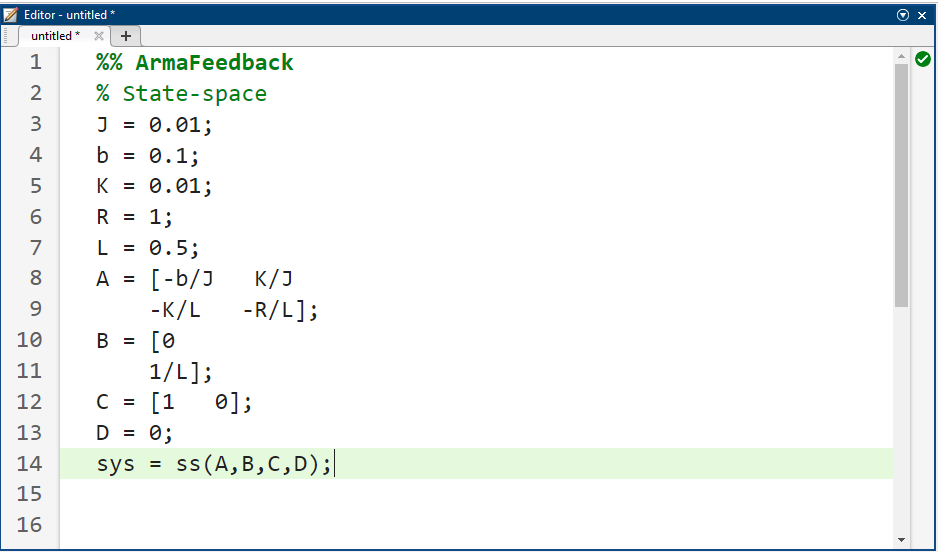
حالا بیایید با استفاده از روشهای معرفی شده، یک کنترلکننده طراحی کنیم. یک فایل m جدید ایجاد کنید و دستورات زیر را در آن تایپ کنید.
کد متلب:
طراحی کنترلکننده فیدبک حالت کامل
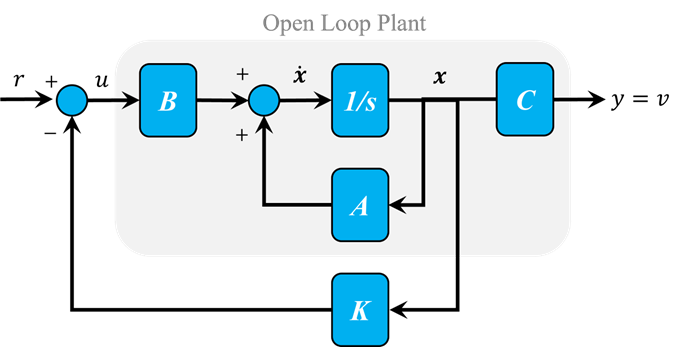
از آنجایی که اندازهگیری هر دو متغیر حالت در مسئله ما آسان است (به سادگی یک آمپرمتر برای جریان و یک تاکومتر برای سرعت اضافه کنید)، میتوانیم یک کنترلکننده فیدبک حالت کامل برای سیستم طراحی کنیم بدون اینکه نگران اضافه کردن یک ناظر باشیم. قانون کنترل برای یک سیستم فیدبک حالت کامل به شکل u = r - Kc x است و شماتیک مربوطه در زیر نشان داده شده است.
به یاد بیاورید که چندجملهای مشخصه برای این سیستم حلقه بسته، دترمینان sI - (A - B Kc) است که در آن s متغیر لاپلاس است. از آنجایی که ماتریسهای A و B Kc هر دو ماتریسهای 2x2 هستند، باید 2 قطب برای سیستم وجود داشته باشد. این واقعیت را میتوان با دستور مرتبه متلب تأیید کرد. اگر سیستم داده شده قابل کنترل باشد، با طراحی یک کنترلکننده فیدبک حالت کامل میتوانیم این دو قطب را به هر جایی که میخواهیم منتقل کنیم. اینکه آیا سیستم داده شده قابل کنترل است یا خیر را میتوان با بررسی رتبه ماتریس کنترلپذیری [B AB A^2B ...] تعیین کرد. دستور ctrb در MATLAB ماتریس کنترلپذیری ماتریسهای A و B داده شده را میسازد.
علاوه بر این، رتبه دستور، رتبه یک ماتریس داده شده را تعیین میکند. دستورات زیر که در خط فرمان اجرا میشوند، مرتبه سیستم و اینکه آیا سیستم قابل کنترل است یا خیر را تأیید میکنند.
کد متلب:
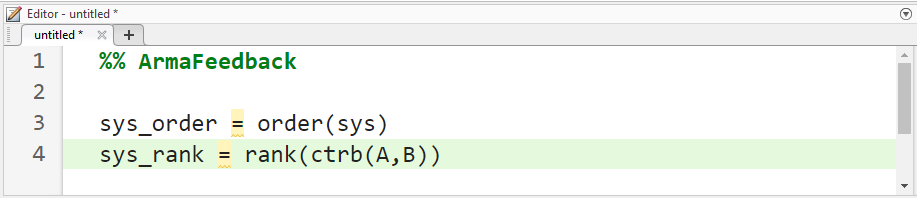
از موارد فوق، میدانیم که سیستم ما کنترلپذیر است زیرا ماتریس کنترلپذیری رتبه کامل دارد. ابتدا قطبها را در -5+i و -5-i قرار میدهیم (توجه داشته باشید که این مربوط به zeta = 0.98 است که نزدیک به 0٪ فراجهش میدهد و sigma = 5 که زمان نشست 0.8 ثانیهای را فراهم میکند). پس از تعیین مکان قطبهای مورد نظر، میتوانیم از دستورات place یا acker در متلب برای تعیین ماتریس بهره کنترلر، Kc، برای دستیابی به این قطبها استفاده کنیم. ما از دستور place استفاده خواهیم کرد زیرا از نظر عددی بهتر از acker است. با این حال، اگر بخواهیم قطبی با کثرت بیشتر از رتبه ماتریس B قرار دهیم، باید از دستور acker استفاده کنیم. کد زیر را به انتهای m-file خود اضافه کنید. اجرا در پنجره فرمان، خروجی ماتریس بهره بازخورد زیر را تولید میکند.
کد متلب:
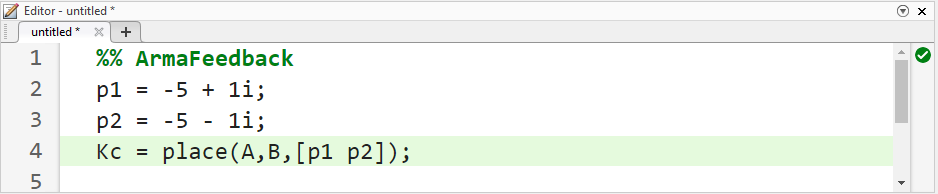
با مراجعه مجدد به معادلات فضای حالت در بالای صفحه، میبینیم که با جایگزینی قانون بازخورد حالت u = r - Kc x به جای u، عبارت زیر حاصل میشود.
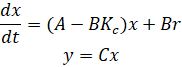
سپس میتوانیم پاسخ حلقه بسته را با اضافه کردن خطوط زیر به انتهای m-file خود مشاهده کنیم. اجرای m-file شما در پنجره فرمان، نموداری را که در زیر نشان داده شده است، نشان میدهد.
کد متلب:
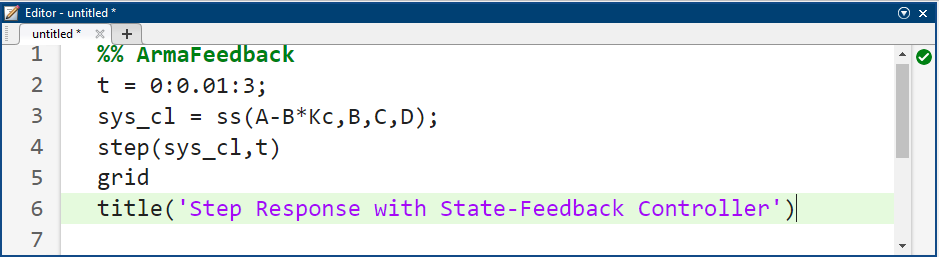
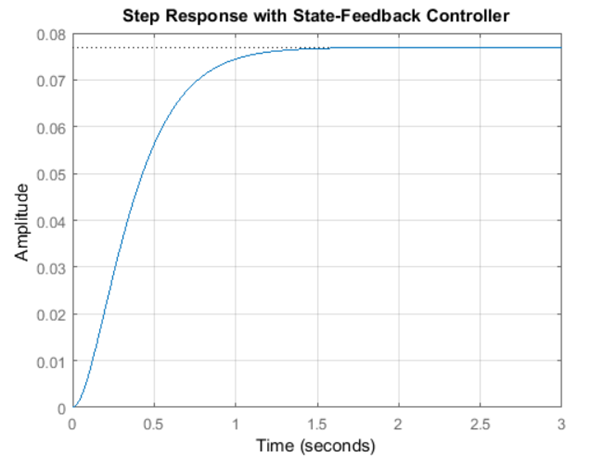
نتیجه شبیهسازی:
افزودن یک پیش جبرانساز
از این نمودار میبینیم که خطای حالت ماندگار بسیار بزرگ است. یک رویکرد برای حذف خطای حالت ماندگار، مقیاسبندی ساده ورودی است تا خروجی نیز به نوبه خود به سطح مطلوب مقیاسبندی شود. این کار در مثال ما کمی چالشبرانگیز است زیرا دو حالت برای بررسی داریم. بنابراین، باید مقادیر حالت ماندگار هر دو حالت را محاسبه کنیم، آنها را در بهره انتخاب شده Kc ضرب کنیم و از نتیجه به عنوان "مرجع" خود برای محاسبه ورودی u استفاده کنیم. این کار را میتوان در یک مرحله با اضافه کردن یک پیش جبرانساز با بهره ثابت روی N بعد از مرجع، همانطور که در شماتیک زیر نشان داده شده است، انجام داد.
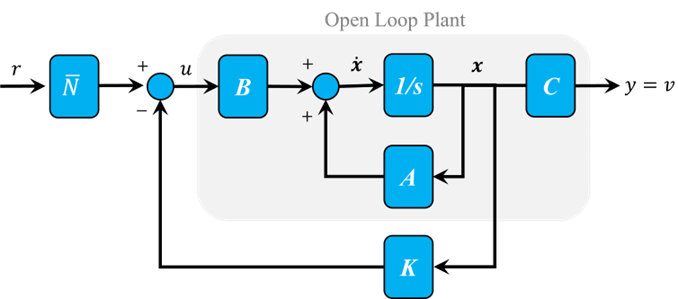
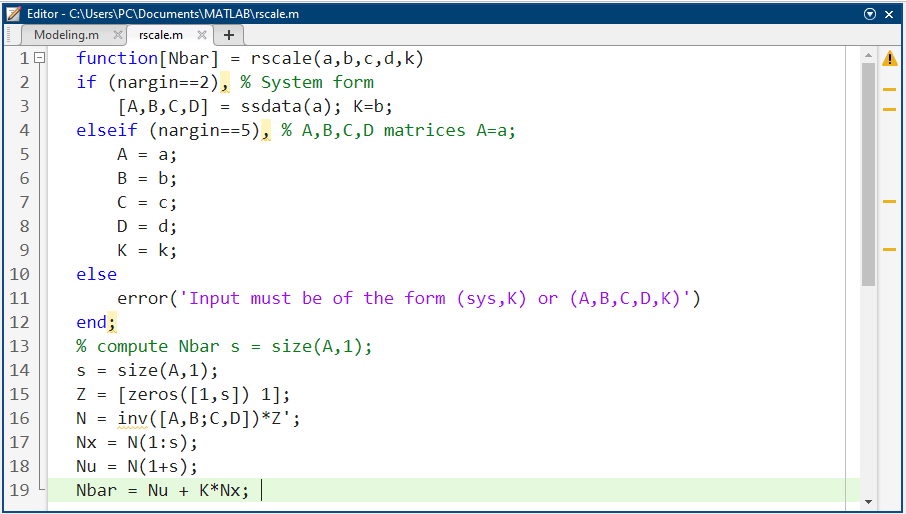
میتوانیم این ضریب N روی خط را با استفاده از تابع تعریفشده توسط کاربر rscale.m مطابق شکل زیر پیدا کنیم. توجه داشته باشید که تابع rscale.m یک تابع استاندارد در متلب نیست. اکنون میتوانید با اضافه کردن خطوط کد بالا و زیر به m-file خود و اجرای مجدد در خط فرمان، پاسخ پله را رسم کنید.
کد متلب:
کد متلب:
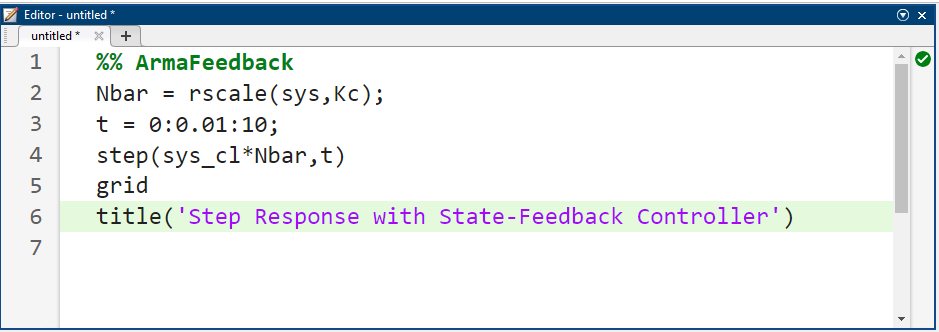
این بار، خطای حالت ماندگار بسیار کمتر از ۱٪ است و تمام معیارهای طراحی دیگر نیز رعایت شدهاند.
نتیجه شبیهسازی:
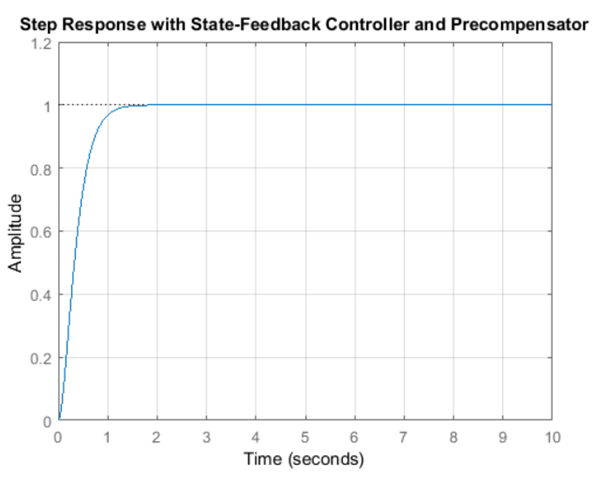
توجه داشته باشید که پیش جبرانساز با خط رویی N که در بالا به کار رفته است، بر اساس مدل نیروگاه محاسبه میشود و علاوه بر این، پیش جبرانساز خارج از حلقه بازخورد قرار دارد. بنابراین، اگر در مدل خطایی (یا اختشاش ناشناخته) وجود داشته باشد، پیش جبرانساز آنها را اصلاح نمیکند و خطای حالت پایدار وجود خواهد داشت. ممکن است به یاد داشته باشید که اضافه کردن کنترل انتگرالی نیز میتواند برای حذف خطای حالت پایدار، حتی در حضور عدم قطعیت مدل و اختلالات پلهای، استفاده شود. برای مثالی از نحوه پیادهسازی کنترل انتگرالی در تنظیمات فضای حالت، به مثال موقعیت موتور DC: روشهای فضای حالت برای طراحی کنترلکننده مراجعه کنید. مزیت استفاده از کنترل انتگرالی این است که خطا ابتدا باید قبل از اینکه بتوان آن را اصلاح کرد، ایجاد شود، بنابراین، سیستم ممکن است در پاسخ دادن کند باشد. از سوی دیگر، پیش جبرانساز قادر است با استفاده از دانش مدل نیروگاه، جبران حالت پایدار را پیشبینی کند. یک تکنیک مفید، ترکیب پیش جبرانساز با کنترل انتگرالی برای بهرهبرداری از مزایای هر رویکرد است.
منابع:
C. H. Houpis, S. N. Sheldon, and J. J. D'Azzo, Linear Control System Analysis and Design, 5th ed. Boca Raton, FL: CRC Press, 2013
Y. Bavafa-Toosi, Introduction to Linear Control Systems. Amsterdam, Netherlands: Elsevier, 2017
K. Ogata, Modern Control Engineering, 5th ed. Upper Saddle River, NJ: Pearson, 2010
N. S. Nise, Control Systems Engineering, 6th ed. Hoboken, NJ: John Wiley & Sons, 2011
C.-T. Chen, Linear System Theory and Design, 3rd ed. New York, NY: Oxford University Press, 1999
G. F. Franklin, J. D. Powell, and A. Emami-Naeini, Feedback Control of Dynamic Systems, 7th ed. Boston, MA: Pearson, 2014
#کنترل_خطی #کنترل_مدرن #کنترل_مقاوم #کنترل_فازی #کنترل_کنترل_هوشمند #کنترل_دیجیتال #کنترل_پیش_بین_مبتنی_بر_مدل #کنترل_بهینه #کنترل_چند_متغییره #کنترل_کلاسیک #کنترل_اتوماتیک #کنترل_عصبی #کنترل_چند_عاملی #کنترل_شبکهای #کنترل_تطبیقی #کنترل #کنترل_غیر_خطی #مهندسی_کنترل #متلب #سیمولینک#متلب_سیمولینک #تابع_تبدیل #معادلات_حالت #مدل_سازی #شبیهسازی #کنترل_مبتنی_بر_داده #کنترل_سیستم #سیستم #بهینه_سازی #سنسور #فیدبک #بازخورد